subsexРасширенная замена
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
subsex(f,old = new, <Unsimplified>) subsex(f,old1 = new1, old2 = new2, …, <Unsimplified>) subsex(f,[old1 = new1, old2 = new2, …], <Unsimplified>) subsex(f,{old1 = new1, old2 = new2, …}, <Unsimplified>) subsex(f, table(old1 = new1, old2 = new2, …), <Unsimplified>) subsex(f,s1, s2, …, <Unsimplified>)
subsex(f, old = new) возвращает копию объекта f в котором все выражения, совпадающие с old заменяются значением new.
subsex возвращает модифицированную копию объекта, но не изменяет сам объект.
subsex(f, old = new) поисковые запросы f для подвыражений, совпадающих с old. Каждое такое подвыражение заменяется new.
В отличие от subs функция, subsex заменяет “неполные” подвыражения. Например, subsex(a + b + c, b + c = d) замены b + c но subs(a + b + c, b + c = d) не заменяет b + c. В общем случае комбинации операндов не “операторы” +, *, and, _exprseqпересечение, or, _lazy_and, _lazy_or, и union может быть заменен. В частности, могут быть заменены частичные суммы и частичные продукты. Обратите внимание на то, что эти операции приняты, чтобы быть коммутативными, например, subsex(a*b*c, a*c = new) действительно заменяет частичный продукт a*c new. Смотрите Пример 1 и Пример 2. Однако преимущество subs по subsex тот subs намного быстрее.
subsex дополнительно степени замен с той же основой, если экспонента выражения является целочисленным кратным заменяющая степень, например, как в subsex(a^4, a^2 = new). Это правило также совпадает с инвертированными выражениями как в subsex(1/sqrt(x), sqrt(x)=new), который внутренне эквивалентен subsex(x^(-1/2), x^(1/2)=new). См. пример 3.
Вызов subsex(f, old1 = new1, old2 = new2, ...) вызывает “sequential substitution”. Смотрите subs страница справки для деталей.
Вызов subsex(f, [old1 = new1, old2 = new2, ...]) вызывает “parallel substitution”. Смотрите subs страница справки для деталей.
Вызов subsex(f, s1, s2, ...) описывает самую общую форму замены, которая может объединить последовательные и параллельные замены. Этот вызов эквивалентен subsex(... subsex(subsex(f, s1), s2), ...). В зависимости от формы s1S2 , …, последовательные или параллельные замены выполняются на каждом шаге. Пример может быть найден на subs страница справки.
После замены не оценен результат. Используйте функциональный eval осуществлять оценку. См. Пример 5.
Операнды последовательностей выражения могут быть заменены subsex. Такие объекты не сглажены. См. Пример 6.
Вызов subsex(f) позволен; это возвращает f без модификаций.
Мы демонстрируем некоторые простые замены; subsex находит и заменяет частичные суммы и продукты:
subsex(a + b + c, a + c = x)
![]()
subsex(a*b*c, a*c = x)
![]()
subsex(a * (b + c) + b + c, b + c = a)
![]()
subsex(a + b*c*d + b*d, b*d = c);
![]()
Мы заменяем подвыражения в символьном объединении множеств:
subsex(a union b union c, a union b = w)
![]()
То же самое может быть достигнуто при помощи функционального эквивалента _union из оператора union:
subsex(_union(a, b, c), _union(a, b) = w)
![]()
Для получения дополнительной информации на функциях замены в MuPAD®, смотрите, Изменяют Подвыражения. Для получения дополнительной информации на деревьях выражений, смотрите, Визуализируют Деревья выражений.
subsex степени замен с с той же основой, если экспонента выражения является целочисленным кратным заменяющая степень:
subsex(1/a^4, a^2 = X)
![]()
Это содержит даже для экспонент, которые являются выражениями:
subsex(1/a^(6*x), a^(2*x) = X)
![]()
1/sqrt(x) внутренне x^(-1/2), так замена sqrt(x) который является внутренне x^(1/2) работает, также:
subsex(1/sqrt(n), sqrt(n) = X)
![]()
subsex часто полезно, чтобы преобразовать выход одной команды в форму, требуемую следующей. Как пример, мы вычисляем Преобразование Лапласа двумерного ОДУ
![]() ,
,
![]() ,
,
и преобразуйте результат в форму, подходящую для вызова solve заменяя неизвестные Преобразования Лапласа символьными именами:
xfrm1 := laplace(x'(t) = x(t) + 2*y(t), t, s); xfrm2 := laplace(y'(t) = 5*x(t) + 2*y(t), t, s)
![]()
![]()
Для удобочитаемости мы даем имена обеим заменам:
sub_x := laplace(x(t),t,s) = X: sub_y := laplace(y(t),t,s) = Y:
Leqn1 := subs(xfrm1, sub_x, sub_y, x(0) = 1); Leqn2 := subs(xfrm2, sub_x, sub_y, y(0) =-2)
![]()
![]()
solve({Leqn1, Leqn2}, {X, Y})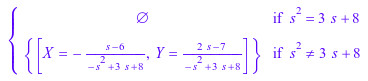
Результат subsex не оценен. В следующем вызове, идентификатор sin не заменяется его значением, т.е. процедурой, задающей поведение синусоидальной функции системы. Следовательно, sin(2*PI) не упрощен до 0 этой процедурой:
subsex(sin(2*x*y), x*y = PI)
![]()
Функциональный eval осуществляет оценку:
eval(subsex(sin(2*x*y), x*y = PI))
![]()
Операндами последовательностей выражения можно подставиться. Обратите внимание на то, что последовательности должны быть заключены в скобках:
subsex((a, b, a*b*c), a*b = x)
![]()
Опция Unsimplified подавляет упрощение:
subsex(2 + a + b, a + b = 0, Unsimplified)
![]()
|
Произвольный объект MuPAD |
|
Произвольные объекты MuPAD |
|
Произвольные объекты MuPAD |
|
Любой уравнения |
|
Предотвращает упрощение возвращенного объекта после замены Как последний шаг замены, модифицированный объект упрощен (однако, не оценен). Эта опция подавляет это итоговое упрощение. Смотрите Пример 7. |
Копия входного объекта с замененными операндами.
f