Документация

И обратные преобразования Фурье Фурье

Существует несколько обычно используемых соглашений для определения преобразований Фурье. MuPAD^® задает преобразование Фурье (FT) как:

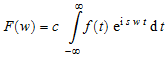
Здесь c и s параметры преобразования Фурье. По умолчанию,   c = 1 и   s = -1. Pref::fourierParameters позволяет вам задать другие значения для этих параметров. Для обратного преобразования Фурье (IFT) MuPAD использует следующее определение:

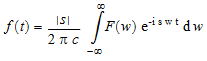
Чтобы вычислить преобразование Фурье арифметического выражения, используйте fourier функция. Например, вычислите преобразования Фурье следующего экспоненциального выражения и распределения дельты Дирака:

fourier(exp(-t^2), t, w),
fourier(dirac(t), t, w)

Если вы знаете преобразование Фурье выражения, можно найти исходное выражение или его математически эквивалентную форму путем вычисления обратного преобразования Фурье. Чтобы вычислить обратное преобразование Фурье, используйте ifourier функция. Например, найдите исходное экспоненциальное выражение и распределение дельты Дирака:

ifourier(PI^(1/2)*exp(-w^2/4), w, t),
ifourier(1, w, t)

Предположим, вы вычисляете преобразование Фурье выражения, и затем вычисляете обратное преобразование Фурье результата. В этом случае MuPAD может возвратить выражение, которое математически эквивалентно исходному, но представленное в другой форме. Например, вычислите преобразования Фурье следующих тригонометрических выражений:

Cosine := fourier(cos(t), t, w);
Sine := fourier(sin(t^2), t, w)

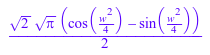
Теперь вычислите обратные преобразования Фурье получившихся выражений Cosine и Sine. Результаты отличаются от исходных выражений:

invCosine := ifourier(Cosine, w, t);
invSine := ifourier(Sine, w, t)

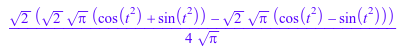
Упрощение получившихся выражений invCosine и invSine дает исходные выражения:

simplify(invCosine), simplify(invSine)

Помимо арифметических выражений, fourier и ifourier функции также принимают матрицы арифметических выражений. Например, вычислите преобразование Фурье следующей матрицы:

A := matrix(2, 2, [exp(-t^2), t*exp(-t^2),
           t^2*exp(-t^2), t^3*exp(-t^2)]):
fourier(A, t, w)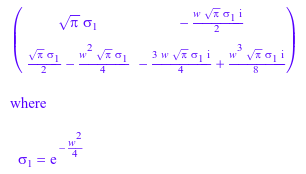

fourier и ifourier функции позволяют вам оценить преобразования выражения или матрицы в конкретной точке. Например, оцените преобразование Фурье матричного A для значений w = 0 и w = 2*x:

fourier(A, t, 0);
fourier(A, t, 2*x)

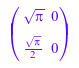
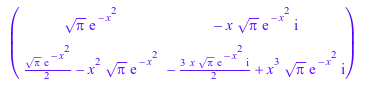
Если MuPAD не может вычислить преобразование Фурье выражения, это возвращается, неразрешенный преобразуйте:

fourier(f(t), t, w)

Если MuPAD не может вычислить обратное преобразование Фурье выражения, это возвращает результат в терминах неразрешенного прямого преобразования Фурье:

ifourier(F(w), w, t)

И обратные преобразования Лапласа Лапласа

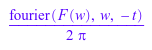
Преобразование Лапласа определяется следующим образом:

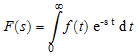Обратное Преобразование Лапласа задано криволинейным интегралом в комплексной плоскости:

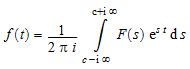где c является действительным значением. Чтобы вычислить Преобразование Лапласа арифметического выражения, используйте laplace функция. Например, вычислите Преобразование Лапласа следующего выражения:

tsine := laplace(t*sin(a*t), t, s)

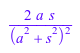
Чтобы вычислить исходное выражение из его Преобразования Лапласа, выполните обратное Преобразование Лапласа. Чтобы вычислить обратное Преобразование Лапласа, используйте ilaplace функция. Например, вычислите обратное Преобразование Лапласа получившегося выражения tsine:

ilaplace(tsine, s, t)

Предположим, вы вычисляете Преобразование Лапласа выражения, и затем вычисляете обратное Преобразование Лапласа результата. В этом случае MuPAD может возвратить выражение, которое математически эквивалентно исходному, но представленное в другой форме. Например, вычислите Преобразования Лапласа следующего выражения:

L := laplace(t*ln(t), t, s)

Теперь вычислите обратное Преобразование Лапласа получившегося выражения L. Результат отличается от исходного выражения:

invL := ilaplace(L, s, t)

Упрощение выражения invL дает исходное выражение:

simplify(invL)

Помимо арифметических выражений, laplace и ilaplace функции также принимают матрицы арифметических выражений. Например, вычислите Преобразование Лапласа следующей матрицы:

A := matrix(2, 2, [1, t, t^2, t^3]):
laplace(A, t, s)

При вычислении преобразования выражения можно использовать предположения на математических свойствах аргументов. Например, вычислите Преобразование Лапласа распределения дельты Дирака:

d := laplace(dirac(t - t_0), t, s) assuming t_0 >=0

Восстановите распределение дельты Дирака от получившегося выражения d:

ilaplace(d, s, t) assuming t_0 >=0

laplace функция обеспечивает преобразования для некоторых специальных функций. Например, вычислите Преобразования Лапласа следующих Функций Бесселя:

laplace(besselJ(0, t), t, s);
laplace(besselJ(1, t), t, s);
laplace(besselJ(1/2, t), t, s)

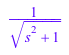
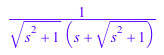
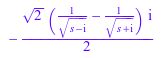
laplace и ilaplace функции позволяют вам оценить преобразования выражения или матрицы в конкретной точке. Например, оцените Преобразование Лапласа следующего выражения для значения s = 10:

laplace(t*exp(-t), t, 10)

Теперь оцените обратное Преобразование Лапласа следующего выражения для значения t = x + y:

ilaplace(1/(1 + s)^2, s, x + y)

Если MuPAD не может вычислить Преобразование Лапласа или обратное Преобразование Лапласа выражения, это возвращается, неразрешенный преобразуйте:

laplace(f(t), t, s)

ilaplace(F(s), s, t)