Пакетное 1D разложение вейвлета
T = wpdec(X,N,wname,E,P)
T = wpdec(X,N,wname)
T = wpdec(X,N,wname,'shannon')
wpdec одномерная пакетная аналитическая функция вейвлета.
T = wpdec(X,N, возвращает пакетное дерево вейвлета wname,E,P)T соответствие пакетному разложению вейвлета векторного X на уровне N, использование вейвлета задано wname (см. wfilters для получения дополнительной информации.
T = wpdec(X,N, эквивалентно wname)T = wpdec(X,N,.wname,'shannon')
E вектор символов или скаляр строки, содержащий тип энтропии и P дополнительный параметр в зависимости от значения T (см. wentropy для получения дополнительной информации.
Энтропийное имя типа (E) | Параметр (P) | Комментарии |
|---|---|---|
'shannon' | P не используется. | |
'log energy' | P не используется. | |
'threshold' | 0P | P порог. |
'sure' | 0P | P порог. |
'norm' | 1P | P степень. |
'user' | вектор символов или скаляр строки | P вектор символов или скаляр строки, содержащий имя файла вашей собственной энтропийной функции, с одним входом X. |
FunName | Никакие ограничения на P |
FunName содержит имя файла вашей собственной энтропийной функции, с X как введено и P как дополнительный параметр к вашей энтропийной функции. |
'user' опция является исторической и все еще сохраненная для совместимости, но это - obsoleted последней опцией, описанной в приведенной выше таблице. FunName опция делает то же самое как 'user' опция и кроме того дает возможность передать параметр вашей собственной энтропийной функции.
Пакетный метод вейвлета является обобщением разложения вейвлета, которое предлагает более богатый анализ сигнала. Пакетные атомы вейвлета являются формами волны, индексированными тремя естественно интерпретированными параметрами: положение и шкала как в разложении вейвлета и частоте.
Для данной ортогональной функции вейвлета сгенерирована библиотека пакетных основ вейвлета. Каждая из этих основ предлагает конкретный способ закодировать сигналы, сохраняя глобальную энергию и восстанавливая точные функции. Пакеты вейвлета могут затем использоваться в многочисленных расширениях данного сигнала.
Простые и эффективные алгоритмы существуют и для пакетного разложения вейвлета и для оптимального выбора разложения. Адаптивные алгоритмы фильтрации с прямыми приложениями в оптимальном кодировании сигнала и сжатии данных могут затем быть произведены.
В ортогональной процедуре разложения вейвлета типовой шаг разделяет коэффициенты приближения в две части. После разделения мы получаем вектор коэффициентов приближения и вектор коэффициентов детали, обоих в более грубой шкале. Информация, потерянная между двумя последовательными приближениями, получена в коэффициентах детали. Следующий шаг состоит в разделении нового вектора коэффициентов приближения; последовательные детали никогда не повторно анализируются.
В соответствующей пакетной ситуации с вейвлетом каждый вектор коэффициентов детали также разложен на две части с помощью того же подхода в качестве в разделении вектора приближения. Это предлагает самый богатый анализ: полное двоичное дерево производится в одномерном случае или четверичном дереве в двумерном случае.
% The current extension mode is zero-padding (see dwtmode).
% Load signal.
load noisdopp; x = noisdopp;
% Decompose x at depth 3 with db1 wavelet packets
% using Shannon entropy.
wpt = wpdec(x,3,'db1','shannon');
% The result is the wavelet packet tree wpt.
% Plot wavelet packet tree (binary tree, or tree of order 2).
plot(wpt)
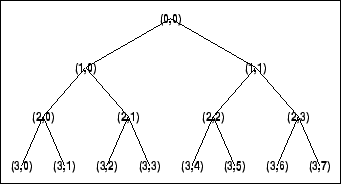
Алгоритм, используемый в пакетном разложении вейвлета, следует за той же линией как процесс разложения вейвлета (см. dwt и wavedec для получения дополнительной информации.
Койфман, R.R.; т-х Викераузер, (1992), “Основанные на энтропии Алгоритмы для лучшего базисного выбора”, Сделка IEEE на Inf. Теория, издание 38, 2, стр 713–718.
Мейер, Y. (1993), Les ondelettes. Algorithmes и приложения, Колин Эд., Париж, 2-й выпуск. (Английский перевод: Вейвлеты: Алгоритмы и Приложения, SIAM).
Wickerhauser, Т-х (1991), “INRIA читает лекции по пакетным алгоритмам вейвлета”, Продолжения ondelettes и paquets d'ondes, 17-21 июня, Rocquencourt, Франция, стр 31–99.
Wickerhauser, Т-х (1994), Адаптированный анализ вейвлета от теории до алгоритмов программного обеспечения, А.К. Питерса.