lqg

Проект "линейного квадратичного гауссова" (LQG)

Синтаксис

reg = lqg(sys,QXU,QWV) reg = lqg(sys,QXU,QWV,QI) reg = lqg(sys,QXU,QWV,QI,'1dof') reg = lqg(sys,QXU,QWV,QI,'2dof') reg = lqg(___,'current') [reg,info] = lqg(___)

Описание

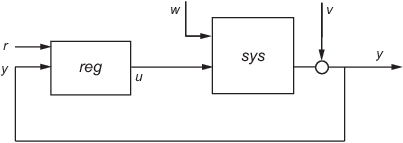
reg = lqg(sys,QXU,QWV) вычисляет оптимальный регулятор "линейного квадратичного гауссова" (LQG) reg учитывая модель в пространстве состояний sys из объекта и матриц взвешивания QXU и QWV. Динамический регулятор reg использует измерения y, чтобы сгенерировать управляющий сигнал u, который регулирует y вокруг нулевого значения. Используйте положительную обратную связь, чтобы соединить этот регулятор с объектом выход y.

Регулятор LQG минимизирует функцию стоимости

$J = E {\lim_{τ \to \infty} \frac{1}{τ} \int_{0}^{τ} [x^{T}, u^{T}] Q_{x u} [\begin{matrix} x \\ u \end{matrix}] d t}$

подвергните уравнениям объекта

$\begin{matrix} d x / d t = A x + B u + w \\ y = C x + D u + v \end{matrix}$

где шум процесса w и шум измерения v является Гауссовыми белыми шумами с ковариацией:

$E ([\begin{matrix} w \\ v \end{matrix}] \cdot [\begin{matrix} w' & v' \end{matrix}]) = Q W V$

reg = lqg(sys,QXU,QWV,QI) использует команду заданного значения r и измерения y, чтобы сгенерировать управляющий сигнал u. reg имеет интегральное действие, чтобы гарантировать, что y отслеживает команду r.

Контроллер сервомотора LQG минимизирует функцию стоимости

$J = E {\lim_{τ \to \infty} \frac{1}{τ} \int_{0}^{τ} ([x^{T}, u^{T}] Q_{x u} [\begin{matrix} x \\ u \end{matrix}] + x_{i}^{T} Q_{i} x_{i}) d t}$

где _xi является интегралом ошибки отслеживания r - y. Для систем MIMO r, y и _xi должны иметь ту же длину.

reg = lqg(sys,QXU,QWV,QI,'1dof') вычисляет один контроллер сервомотора степени свободы, который берет e = r - y, а не [r; y], как введено.

reg = lqg(sys,QXU,QWV,QI,'2dof') эквивалентно LQG(sys,QXU,QWV,QI) и производит два контроллера сервомотора степени свободы, показанные ранее.

reg = lqg(___,'current') использует "текущую" Оценку состояния фильтра Калмана, которая использует x [n |n] как оценка состояния при вычислении регулятора LQG для системы дискретного времени.

[reg,info] = lqg(___) возвращает контроллер и матрицы усиления средства оценки в структуре info для любого из предыдущих синтаксисов. Можно использовать контроллер и усиления средства оценки к, например, реализовать контроллер в форме наблюдателя. Для получения дополнительной информации см. Алгоритмы.

Примеры

Регулятор "линейного квадратичного гауссова" (LQG) и проектирование контроллера сервомотора

В этом примере показано, как спроектировать регулятор "линейного квадратичного гауссова" (LQG), одна степень свободы контроллер сервомотора LQG и две степени свободы контроллер сервомотора LQG для следующей системы.

Объект имеет три состояния (x), два входных параметров управления (u), три случайных входных параметров (w), один выход (y), шум измерения для выхода (v), и следующее состояние и уравнения измерения.

$\begin{array}{l} \frac{d x}{d t} = A x + B u + w \\ y = C x + D u + v \end{array}$

где

$\begin{array}{l} A = [\begin{matrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{matrix}] B = [\begin{matrix} 0.3 & 1 \\ 0 & 1 \\ - 0.3 & 0.9 \end{matrix}] \\ C = [\begin{matrix} 1.9 & 1.3 & 1 \end{matrix}] D = [\begin{matrix} 0.53 & - 0.61 \end{matrix}] \end{array}$

Система имеет следующие шумовые данные о ковариации:

$\begin{array}{l} Q_{n} = E (w w^{T}) = [\begin{matrix} 4 & 2 & 0 \\ 2 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}] \\ R_{n} = E (v v^{T}) = 0.7 \end{array}$

Для регулятора используйте следующую функцию стоимости, чтобы задать компромисс между производительностью регулирования и усилием по управлению:

$J (u) = \int_{0}^{\infty} (0.1 x^{T} x + u^{T} [\begin{matrix} 1 & 0 \\ 0 & 2 \end{matrix}] u) d t$

Для контроллеров сервомотора используйте следующую функцию стоимости, чтобы задать компромисс между производительностью средства отслеживания и усилием по управлению:

$J (u) = \int_{0}^{\infty} (0.1 x^{T} x + x_{i}^{2} + u^{T} [\begin{matrix} 1 & 0 \\ 0 & 2 \end{matrix}] u) d t$

Спроектировать контроллеры LQG для этой системы:

Создайте систему в пространстве состояний путем ввода следующего в Окне Команды MATLAB:
```
A = [0 1 0;0 0 1;1 0 0];    
B = [0.3 1;0 1;-0.3 0.9];
C = [1.9 1.3 1];  
D = [0.53 -0.61];
sys = ss(A,B,C,D);
```

Задайте шумовые данные о ковариации и матрицы взвешивания путем ввода следующих команд:

nx = 3;    %Number of states
ny = 1;    %Number of outputs
Qn = [4 2 0; 2 1 0; 0 0 1];
Rn = 0.7;
R = [1 0;0 2]
QXU = blkdiag(0.1*eye(nx),R);
QWV = blkdiag(Qn,Rn);
QI = eye(ny);

Сформируйте регулятор LQG путем ввода следующей команды:

KLQG = lqg(sys,QXU,QWV)

Эта команда возвращает следующий регулятор LQG:

A = 
           x1_e    x2_e    x3_e
   x1_e  -6.212  -3.814  -4.136
   x2_e  -4.038  -3.196  -1.791
   x3_e  -1.418  -1.973  -1.766
 
B = 
             y1
   x1_e   2.365
   x2_e   1.432
   x3_e  0.7684
 
C = 
            x1_e       x2_e       x3_e
   u1   -0.02904  0.0008272     0.0303
   u2    -0.7147    -0.7115    -0.7132
 
D = 
       y1
   u1   0
   u2   0
 
Input groups:              
       Name        Channels
    Measurement       1    
                           
Output groups:             
      Name      Channels   
    Controls      1,2      
                           
Continuous-time model.

Сформируйте одну степень свободы контроллер сервомотора LQG путем ввода следующей команды:

KLQG1 = lqg(sys,QXU,QWV,QI,'1dof')

Эта команда возвращает следующий контроллер сервомотора LQG:

A = 
           x1_e    x2_e    x3_e     xi1
   x1_e  -7.626  -5.068  -4.891  0.9018
   x2_e  -5.108  -4.146  -2.362  0.6762
   x3_e  -2.121  -2.604  -2.141  0.4088
   xi1        0       0       0       0
 
B = 
              e1
   x1_e   -2.365
   x2_e   -1.432
   x3_e  -0.7684
   xi1         1
 
C = 
          x1_e     x2_e     x3_e      xi1
   u1  -0.5388  -0.4173  -0.2481   0.5578
   u2   -1.492   -1.388   -1.131   0.5869
 
D = 
       e1
   u1   0
   u2   0
 
Input groups:           
    Name     Channels   
    Error       1       
                        
Output groups:          
      Name      Channels
    Controls      1,2   
                        
Continuous-time model.

Сформируйте две степени свободы контроллер сервомотора LQG путем ввода следующей команды:

KLQG2 = lqg(sys,QXU,QWV,QI,'2dof')

Эта команда возвращает следующий контроллер сервомотора LQG:

A = 
           x1_e    x2_e    x3_e     xi1
   x1_e  -7.626  -5.068  -4.891  0.9018
   x2_e  -5.108  -4.146  -2.362  0.6762
   x3_e  -2.121  -2.604  -2.141  0.4088
   xi1        0       0       0       0
 
B = 
             r1      y1
   x1_e       0   2.365
   x2_e       0   1.432
   x3_e       0  0.7684
   xi1        1      -1
 
C = 
          x1_e     x2_e     x3_e      xi1
   u1  -0.5388  -0.4173  -0.2481   0.5578
   u2   -1.492   -1.388   -1.131   0.5869
 
D = 
       r1  y1
   u1   0   0
   u2   0   0
 
Input groups:              
       Name        Channels
     Setpoint         1    
    Measurement       2    
                           
Output groups:             
      Name      Channels   
    Controls      1,2      
                           
Continuous-time model.

Советы

lqg может использоваться и в непрерывном - и в объекты дискретного времени. В дискретное время, lqg использование x [n |n-1] как его оценка состояния по умолчанию. Чтобы использовать x [n |n] как оценка состояния и вычислить оптимальный контроллер LQG, используйте 'current' входной параметр. Для получения дополнительной информации на средствах оценки состояния, смотрите kalman.
Вычислить регулятор LQG, lqg использует команды lqr и kalman. Вычислить контроллер сервомотора, lqg использует команды lqi и kalman.
Когда это необходимо, больше гибкости для разработки регуляторов, можно использовать lqr, kalman, и lqgreg команды. Когда это необходимо, больше гибкости для разработки контроллеров сервомотора, можно использовать lqi, kalman, и lqgtrack команды. Для получения дополнительной информации об использовании этих команд и как решить, когда использовать их, см. Проект "линейного квадратичного гауссова" (LQG) для Регулирования и Проект "линейного квадратичного гауссова" (LQG) Контроллера Сервомотора с Интегральным Действием.

Алгоритмы

Уравнения контроллера:

В течение непрерывного времени:
$\begin{matrix} d x_{e} = A x_{e} + B u + L (y - C x_{e} - D u) \\ u = - K_{x} x_{e} - K_{i} x_{i} \end{matrix}$
В течение дискретного времени:
$x [n + 1 | n] = A x [n | n - 1] + B u [n] + L (y [n] - C x [n | n - 1] - D u [n])$
- Задержанное средство оценки:
  $u [n] = - K_{x} x [n | n - 1] - K_{i} x_{i} [n]$
- Текущее средство оценки:
  $\begin{matrix} u [n] = - K_{x} x [n | n] - K_{i} x_{i} [n] - K_{w} w [n | n] \\ = - K_{x} x [n | n - 1] - K_{i} x_{i} [n] - (K_{x} M_{x} + K_{w} M_{w}) y_{i n n} [n] \end{matrix}$
  $y_{i n n} [n] = y [n] - C x [n | n - 1] - D u [n]$

Здесь,

A, B, C и D являются матрицами пространства состояний регулятора LQG, reg.
_xi является интегралом ошибки отслеживания r - y.
_Kx, _Kw, _Ki, L, _Mx и _Mw являются контроллером и матрицами усиления средства оценки, возвращенными в info.

Смотрите также

care | dare | kalman | lqi | lqr | lqry | ss

Документация

lqg

Синтаксис

Описание

Примеры

Советы

Алгоритмы

Смотрите также

Представлено до R2006a

Документация Control System Toolbox

Поддержка