Находящиеся на диске запасы устойчивости обратной связи
[ вычисляет находящиеся на диске запасы устойчивости для SISO или цикла отрицательной обратной связи MIMO DM,MM] = diskmargin(L)feedback(L,eye(N)), где N количество вводов и выводов в L.
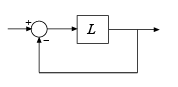
diskmargin команда возвращает цикл за один раз запасы устойчивости в DM и многоконтурные поля в MM. Находящийся на диске граничный анализ обеспечивает более сильную гарантию устойчивости, чем классические запасы по амплитуде и фазе. Для получения общей информации о дисковых полях, смотрите, что Анализ Устойчивости Использует Дисковые Поля.
___ = diskmargin(___, задает дополнительный параметр эксцентриситета, который смещает смоделированное усиление и изменение фазы к увеличению усиления (положительный E)E) или получите уменьшение (отрицательный E). Можно использовать этот аргумент, чтобы протестировать относительную чувствительность запасов устойчивости, чтобы получить увеличения по сравнению с уменьшениями. Можно использовать этот аргумент с любым из предыдущих синтаксисов.
diskmargin вычисляет и цикл за один раз и многоконтурные дисковые поля. Этот пример иллюстрирует, что цикл за один раз поля может дать чрезмерно оптимистическую оценку истинной робастности обратной связи MIMO. Поля отдельных циклов могут быть чувствительны к небольшим возмущениям в других циклах и цикле за один раз, поля игнорируют такие взаимодействия цикла.
Рассмотрите двухканальную обратную связь MIMO следующего рисунка.

Модель объекта управления P чертится от Запасов устойчивости MIMO для Вращения Спутника и C статическое усиление выходной обратной связи [1 - 2; 0 1].
a = [0 10;-10 0]; b = eye(2); c = [1 10;-10 1]; P = ss(a,b,c,0); C = [1 -2;0 1];
Вычислите находящиеся на диске поля на объекте выход. Ответом разомкнутого цикла отрицательной обратной связи на объекте выход является Lo = P*C.
Lo = P*C; [DMo,MMo] = diskmargin(Lo);
Исследуйте цикл за один раз дисковые поля, возвращенные в массиве структур DM. Каждая запись в DM содержит запасы устойчивости соответствующего канала обратной связи.
DMo(1)
ans = struct with fields:
GainMargin: [0 Inf]
PhaseMargin: [-90 90]
DiskMargin: 2
LowerBound: 2
UpperBound: 2
Frequency: Inf
WorstPerturbation: [2x2 ss]
DMo(2)
ans = struct with fields:
GainMargin: [0 Inf]
PhaseMargin: [-90 90]
DiskMargin: 2
LowerBound: 2
UpperBound: 2
Frequency: 0
WorstPerturbation: [2x2 ss]
Цикл за один раз поля превосходен (бесконечный запас по амплитуде и запас по фазе на 90 °). Затем исследуйте многоконтурные дисковые поля MMo. Они считают независимое и параллельное усиление (фаза) изменениями обеих обратной связи. Это - более реалистическая оценка, потому что неопределенность объекта обычно влияет на оба канала одновременно.
MMo
MMo = struct with fields:
GainMargin: [0.6839 1.4621]
PhaseMargin: [-21.2607 21.2607]
DiskMargin: 0.3754
LowerBound: 0.3754
UpperBound: 0.3762
Frequency: 0
WorstPerturbation: [2x2 ss]
Многоконтурные запасы по амплитуде и фазе намного более слабы, чем их цикл за один раз дубликаты. Устойчивость только гарантируется, когда усиление в каждом цикле будет варьироваться фактором меньше чем 1,46, или когда фаза каждого цикла варьируется меньше чем на 21 °. Используйте diskmarginplot визуализировать запасы по амплитуде и фазе как функцию частоты.
diskmarginplot(Lo)

Как правило, существует неопределенность и в приводах (входные параметры) и в датчиках (выходные параметры). Поэтому это - хорошая идея вычислить дисковые поля во входных параметрах объекта, а также выходных параметрах. Используйте Li = C*P вычислить поля во входных параметрах объекта. Для этой системы поля являются тем же самым при вводах и выводах объекта.
Li = C*P; [DMi,MMi] = diskmargin(Li); MMi
MMi = struct with fields:
GainMargin: [0.6839 1.4621]
PhaseMargin: [-21.2607 21.2607]
DiskMargin: 0.3754
LowerBound: 0.3754
UpperBound: 0.3762
Frequency: 0
WorstPerturbation: [2x2 ss]
Наконец, можно также вычислить многоконтурные дисковые поля для усиления или изменений фазы в обоих вводы и выводы объекта. Этот подход является самой полной оценкой запасов устойчивости, потому что это это рассматривает независимое и параллельное усиление или изменения фазы всех каналов ввода и вывода. Как ожидалось, всех трех мер, это дает самые маленькие запасы по амплитуде и фазе.
MMio = diskmargin(P,C); diskmarginplot(MMio.GainMargin)

Устойчивость только гарантируется, когда усиление будет варьироваться меньше чем на 2 дБ или когда фаза варьируется меньше чем на 13 °. Однако эти изменения происходят во входных параметрах и выходных параметрах P, таким образом, общее изменение в усилении ввода-вывода или фазе - дважды это.
По умолчанию, diskmargin вычисляет симметричный запас по амплитуде, с gmin = 1/gmax, и связанный запас по фазе. В некоторых системах, однако, устойчивость цикла может быть более чувствительна к увеличениям или уменьшениям в коэффициенте усиления разомкнутого контура. Используйте параметр эксцентриситета E, чтобы исследовать эту чувствительность.
Вычислите дисковое поле, и сопоставил находящиеся на диске запасы по амплитуде и фазе для передаточной функции SISO, в трех значениях E. Отрицательный E смещает расчет к уменьшению усиления. Положительный E смещает к увеличению усиления.
L = tf(25,[1 10 10 10]); DMdec = diskmargin(L,-2); DMbal = diskmargin(L,0); DMinc = diskmargin(L,2); DGMdec = DMdec.GainMargin
DGMdec = 1×2
0.4013 1.3745
DGMbal = DMbal.GainMargin
DGMbal = 1×2
0.6273 1.5942
DGMinc = DMinc.GainMargin
DGMinc = 1×2
0.7717 1.7247
Соедините, эти результаты показывают, что в отсутствие изменения фазы, устойчивость обеспечена для относительных изменений усиления между 0,4 и 1.72. Чтобы видеть, как запас по фазе зависит от этих изменений усиления, постройте устойчивые области значений усиления и изменений фазы для каждого diskmargin результат.
diskmarginplot([DGMdec;DGMbal;DGMinc]) legend('E = -2','E = 0','E = 2') title('Stable range of gain and phase variations')

Этот график показывает, что обратная связь может терпеть большие изменения фазы, когда усиление уменьшается. Другими словами, устойчивость цикла более чувствительна, чтобы получить увеличение. Несмотря на то, что E = –2 урожая запас по фазе, столь же большой как 30 градусов, это большое значение принимает маленькое увеличение усиления меньше чем 3 дБ. Однако график показывает это, когда увеличения усиления на 4 дБ, запас по фазе спадает меньше чем до 15 градусов. В отличие от этого, остается больше, чем 30 градусов, когда усиление уменьшается на 4 дБ.
Таким образом варьируясь эксцентриситет E может дать более полное изображение чувствительности к неопределенности фазы и усилению. Если вы в основном не обеспокоены изменениями усиления одного направления (увеличение или уменьшение), не рекомендуется сделать выводы из одного ненулевого значения E. Вместо этого используйте значение по умолчанию E = 0, чтобы получить объективные оценки запасов по амплитуде и фазе. При использовании ненулевых значений E используйте и положительные и отрицательные величины, чтобы сравнить относительную чувствительность, чтобы получить увеличение и уменьшение.
L — Ответ разомкнутого циклаОтвет разомкнутого цикла в виде модели динамической системы. L может быть SISO или MIMO, пока это имеет то же количество вводов и выводов. diskmargin вычисляет находящиеся на диске запасы устойчивости для отрицательной обратной связи система с обратной связью feedback(L,eye(N)).

Вычислить дисковые поля системы положительной обратной связи feedback(L,eye(N),+1), используйте diskmargin(-L).
Когда у вас есть контроллер P и объект C, можно вычислить дисковые поля для усиления (или фаза) изменения при вводах или выводах объекта, как в следующей схеме.
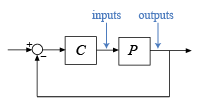
Чтобы вычислить поля на объекте выходные параметры, установите L = P*C.
Чтобы вычислить поля во входных параметрах объекта, установите L = C*P.
L может быть непрерывное время или дискретное время. Если L обобщенная модель в пространстве состояний (genss или uss) затем diskmargin использует текущее значение или номинальную стоимость всех блоков системы управления в L.
Если L модель данных частотной характеристики (такая как frd), затем diskmargin вычисляет поля на каждой частоте, представленной в модели. Функция возвращает поля на частоте с самым маленьким дисковым полем.
Если L массив моделей, затем diskmargin вычисляет поля для каждой модели в массиве.
P — ОбъектОбъект в виде модели динамической системы. P может быть SISO или MIMO, настолько же долго как P*C имеет то же количество вводов и выводов. diskmargin вычисляет находящиеся на диске запасы устойчивости для отрицательной обратной связи система с обратной связью. Чтобы вычислить дисковые поля системы с положительной обратной связью, используйте diskmargin(P,-C).
P может быть непрерывное время или дискретное время. Если P обобщенная модель в пространстве состояний (genss или uss) затем diskmargin использует текущее значение или номинальную стоимость всех блоков системы управления в P.
Если P модель данных частотной характеристики (такая как frd), затем diskmargin вычисляет поля на каждой частоте, представленной в модели. Функция возвращает поля на частоте с самым маленьким дисковым полем.
C — КонтроллерКонтроллер в виде модели динамической системы. C может быть SISO или MIMO, настолько же долго как P*C имеет то же количество вводов и выводов. diskmargin вычисляет находящиеся на диске запасы устойчивости для отрицательной обратной связи система с обратной связью. Чтобы вычислить дисковые поля системы с положительной обратной связью, используйте diskmargin(P,-C).
C может быть непрерывное время или дискретное время. Если C обобщенная модель в пространстве состояний (genss или uss) затем diskmargin использует текущее значение или номинальную стоимость всех блоков системы управления в C.
Если C модель данных частотной характеристики (такая как frd), затем diskmargin вычисляет поля на каждой частоте, представленной в модели. Функция возвращает поля на частоте с самым маленьким дисковым полем.
E — ЭксцентриситетЭксцентриситет области неопределенности использовался для расчета запасов устойчивости в виде действительного скалярного значения. Этот параметр смещает неопределенность, используемую, чтобы смоделировать усиление и изменения фазы к увеличению усиления или уменьшению усиления.
E по умолчанию = 0 использования сбалансированная модель изменения усиления области значений [gmin,gmax], с gmin = 1/gmax.
Положительный E использует модель с большим количеством увеличения усиления, чем уменьшение (gmax > 1/gmin).
Отрицательный E использует модель с большим количеством уменьшения усиления, чем увеличение (gmin < 1/gmax).
Используйте значение по умолчанию E = 0, чтобы получить объективные оценки запасов по амплитуде и фазе. Можно протестировать относительную чувствительность, чтобы получить увеличение и уменьшение путем сравнения полей, полученных и с положительными и с отрицательными значениями E. Для примера смотрите Чувствительность Находящихся на диске Полей, чтобы Получить Увеличение и Уменьшение. Для более подробной информации, о как выбор E влияет на граничный расчет, смотрите, что Анализ Устойчивости Использует Дисковые Поля.
DM — Дисковые поля для каждого канала обратной связиДисковые поля для каждого канала обратной связи со всеми другими замкнутыми кругами, возвратились как структура для обратной связи SISO или N-by-1 массив структур для цикла MIMO с каналами обратной связи N. Поля DM(i) :
| Поле | Значение |
|---|---|
GainMargin | Находящиеся на диске запасы по амплитуде соответствующего канала обратной связи, возвращенного как вектор формы [gmin,gmax]. Этот экспресс значений в абсолютных единицах сумма, которой усиление цикла в том канале может уменьшиться или увеличиться при сохранении устойчивости. Например, если DM(i).GainMargin = [0.8,1.25] затем усиление i th цикл может быть умножено на любой фактор между 0,8 и 1.25, не вызывая нестабильность. Когда E = 0, gmin = 1/gmax. Если коэффициент усиления разомкнутого контура может изменить знак без потери устойчивости, gmin может быть меньше нуля для достаточно большого отрицательного E. Если номинальная система с обратной связью нестабильна, то DM(i).GainMargin = [1 1]. |
PhaseMargin | Находящийся на диске запас по фазе соответствующего канала обратной связи, возвращенного как вектор формы [-pm,pm] в градусах. Эти значения выражают сумму, которой фаза цикла в том канале может уменьшиться или увеличиться при сохранении устойчивости. Если система с обратной связью нестабильна, то DM(i).PhaseMargin = [0 0]. |
DiskMargin | Максимальный ɑ, совместимый с устойчивостью с обратной связью для соответствующего канала обратной связи. ɑ параметрирует неопределенность в ответе цикла (см. Алгоритмы). Если система с обратной связью нестабильна, то DM(i).DiskMargin = 0. |
LowerBound | Нижняя граница на дисковом поле. Это значение совпадает с DiskMargin. |
UpperBound | Верхняя граница на дисковом поле. Это значение представляет верхний предел поля фактической дисковой емкости системы. Другими словами, дисковое поле, как гарантируют, будет не хуже, чем LowerBound и не лучше, чем UpperBound. |
Frequency | Частота, на которой самое слабое поле происходит для соответствующего канала цикла. Это значение находится в rad/TimeUnit, где TimeUnit TimeUnit свойство L. |
WorstPerturbation | Самое маленькое усиление и изменение фазы, которое управляет нестабильной обратной связью, возвратились как пространство состояний (
Эта модель в пространстве состояний является диагональным возмущением формы При анализе линейной аппроксимации нелинейной системы может быть полезно ввести |
Когда L = P*C ответ разомкнутого цикла системы, включающей контроллер и объект с модульной отрицательной обратной связью в каждом канале, DM содержит запасы устойчивости для изменений на объекте выходные параметры. Чтобы вычислить запасы устойчивости для изменений во входных параметрах объекта, используйте L = C*P. Чтобы вычислить запасы устойчивости для одновременных, независимых изменений в обоих вводы и выводы объекта, используйте MMIO = diskmargin(P,C).
Когда L массив моделей, DM имеет дополнительные размерности, соответствующие измерениям массива L. Например, если L 1 3 массив 2D входа, 2D выходных моделей, затем DM 2 3 массив структур. DM(j,k) содержит поля для j th канал обратной связи k th модель в массиве.
MM — Многоконтурные дисковые поляМногоконтурные дисковые поля, возвращенные как структура. Усиление (или фаза) поля определяют количество, сколько изменения усиления (или изменения фазы) система может терпеть во всех каналах обратной связи целиком при оставлении устойчивой. Таким образом, MM одна структура независимо от количества каналов обратной связи в системе. (Для систем SISO, MM = DM.) Поля MM :
| Поле | Значение |
|---|---|
GainMargin | Многоконтурные находящиеся на диске запасы по амплитуде, возвращенные как вектор формы [gmin,gmax]. Эти значения выражают в абсолютных единицах сумму, которой усиление цикла может варьироваться по всем каналам независимо и одновременно при сохранении устойчивости. Например, если MM.GainMargin = [0.8,1.25] затем усиление всех циклов может быть умножено на любой фактор между 0,8 и 1.25, не вызывая нестабильность. Когда E = 0, gmin = 1/gmax. |
PhaseMargin | Многоконтурный находящийся на диске запас по фазе, возвращенный как вектор формы [-pm,pm] в градусах. Эти значения выражают сумму, которой фаза цикла может варьироваться по всем каналам независимо и одновременно при сохранении устойчивости. |
DiskMargin | Максимальный ɑ, совместимый с устойчивостью с обратной связью. ɑ параметрирует неопределенность в ответе цикла (см. Алгоритмы). |
LowerBound | Нижняя граница на дисковом поле. Это значение совпадает с DiskMargin. |
UpperBound | Верхняя граница на дисковом поле. Это значение представляет верхний предел поля фактической дисковой емкости системы. Другими словами, дисковое поле, как гарантируют, будет не хуже, чем LowerBound и не лучше, чем UpperBound. |
Frequency | Частота, на которой происходит самое слабое поле. Это значение находится в rad/TimeUnit, где TimeUnit TimeUnit свойство L. |
WorstPerturbation | Самое маленькое усиление и изменение фазы, которое управляет нестабильной обратной связью, возвратились как пространство состояний (
Эта модель в пространстве состояний является диагональным возмущением формы При анализе линейной аппроксимации нелинейной системы может быть полезно ввести |
Когда L = P*C ответ разомкнутого цикла системы, включающей контроллер и объект с модульной отрицательной обратной связью в каждом канале, MM содержит запасы устойчивости для изменений на объекте выходные параметры. Чтобы вычислить запасы устойчивости для изменений во входных параметрах объекта, используйте L = C*P. Чтобы вычислить запасы устойчивости для одновременных, независимых изменений в обоих вводы и выводы объекта, используйте MMIO = diskmargin(P,C).
Когда L массив моделей, MM массив структур с одной записью для каждой модели в L.
MMIO — Дисковые поля для независимых изменений всех каналов ввода и выводаДисковые поля для независимых изменений, примененных одновременно в каналах ввода и вывода объекта P, возвращенный как структура, имеющая те же поля как MM.
Для изменений, примененных одновременно при вводах и выводах, WorstPerturbation поле является самостоятельно структурой с полями Input и Output. Каждое из этих полей содержит модель в пространстве состояний, таким образом это для Fi(s) = MMIO.WorstPerturbation.Input и Fo(s) = MMIO.WorstPerturbation.Output, система следующей схемы незначительно нестабильна с полюсом на контуре устойчивости на частоте MMIO.Frequency.
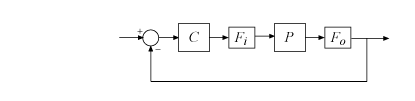
Эти модели в пространстве состояний Input и Output диагональные возмущения формы F(s) = diag(f1(s),...,fN(s)). Каждый fj(s) динамическая система действительного параметра, которая понимает усиление комплекса худшего случая, и изменение фазы применилось к каждому каналу обратной связи.
diskmargin принимает отрицательную обратную связь. Чтобы вычислить дисковые поля системы положительной обратной связи, используйте diskmargin(-L) или diskmargin(P,-C).
Чтобы вычислить дисковые поля для системы, смоделированной в Simulink®, сначала линеаризуйте модель, чтобы получить ответ разомкнутого цикла в конкретной рабочей точке. Затем используйте diskmargin вычислить запасы устойчивости для линеаризованной системы. Для получения дополнительной информации смотрите Запасы устойчивости Модели Simulink.
Чтобы вычислить классические запасы по амплитуде и фазе, используйте allmargin.
Можно визуализировать дисковые поля с помощью diskmarginplot.
diskmargin вычисляет запасы по амплитуде и фазе путем применения находящейся на диске модели неопределенности, чтобы представлять усиление и изменения фазы, и затем нахождения самого большого таким диском, для которого система с обратной связью устойчива.
Для SISO L модель неопределенности для граничного диском анализа включает мультипликативную комплексную неопределенность F в передаточную функцию цикла можно следующим образом:
Здесь,
δ является ограниченной усилением динамической неопределенностью, нормированной так, чтобы он всегда варьировался в единичном диске (|δ | <1).
α устанавливает сумму усиления и изменения фазы, смоделированного F. Для фиксированного E параметр ɑ управляет размером диска. Для α = 0, мультипликативный фактор равняется 1, соответствуя номинальному L.
E, названный eccentricity, скашивает смоделированную неопределенность к увеличению усиления или уменьшению усиления. (Для получения дополнительной информации об эффекте эксцентриситета на модели неопределенности, смотрите, что Анализ Устойчивости Использует Дисковые Поля.)
Для систем MIMO модель позволяет неопределенности варьироваться независимо по каждому каналу:
Модель заменяет ответ разомкнутого цикла MIMO L на L *F, где
Для данного E, disk margin является самый большой ɑ для который система с обратной связью feedback(L*F,1) (или feedback(L*F,eye(N)) для систем MIMO), устойчиво для всех значений F. Найти это значение, diskmargin решает устойчивую задачу устойчивости: Найдите самый большой α таким образом, что система с обратной связью устойчива для всего F в диске неопределенности Δ (α, E) описанный
В случае SISO устойчивый анализ устойчивости приводит к
где S является функцией чувствительности (1 + L) –1 .
В случае MIMO устойчивый анализ устойчивости приводит к
Здесь, μ Δ является структурированным сингулярным значением (mussv) для диагональной структуры
и δj является нормированной неопределенностью для каждого Fj.
Для получения дополнительной информации о граничном расчете, смотрите Раздел 6 в [1].
Поведение изменяется в R2020a
diskmargin команда возвращает находящиеся на диске запасы по амплитуде в GainMargin поле его структур output DM, MM, и MMIO. Эти поля принимают форму [gmin,gmax], подразумевать, что коэффициент усиления разомкнутого контура может быть умножен на любого, включает ту область значений без потери устойчивости с обратной связью. Начинаясь в R2020a, более низком уровне области значений gmin может быть отрицательным для некоторых отрицательных величин эксцентриситета E, если система с обратной связью остается устойчивой, даже если знак коэффициента усиления разомкнутого контура изменяется. Эксцентриситет управляет смещением в находящемся на диске запасе по амплитуде к уменьшению усиления или увеличению (см., что Анализ Устойчивости Использует Дисковые Поля). Ранее область значений запаса по амплитуде была всегда положительна.
[1] Загубите, степень доктора юридических наук, Р.Л. Дэйли, и Д. Гэнгсаас. "Практический Проект Закона о надзоре для Самолета Используя Многомерные Методы". Международный журнал Управления. Издание 59, Номер 1, 1994, стр 93–137.
allmargin | diskmargin | diskmarginplot | margin | wcdiskmargin | wcdiskmarginplot
У вас есть модифицированная версия этого примера. Вы хотите открыть этот пример со своими редактированиями?
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.