Вероятностные распределения являются теоретическими распределениями на основе предположений об исходной совокупности. Распределения определяют вероятность событию, что случайная переменная имеет определенное, дискретное значение или находится в пределах заданной области непрерывных значений.
Statistics and Machine Learning Toolbox™ предлагает несколько способов работать с вероятностными распределениями.
Используйте Функции распределения вероятностей, чтобы работать с вводом данных из матриц.
Используйте Приложения Распределения вероятностей и Пользовательские интерфейсы, чтобы в интерактивном режиме строить, исследовать и генерировать случайные числа от вероятностных распределений. Доступные приложения и пользовательские интерфейсы включают:
Приложение Distribution Fitter
Пользовательский интерфейс Probability Distribution Function
Пользовательский интерфейс Генерации случайных чисел (randtool)
Для списка распределений, поддержанных Statistics and Machine Learning Toolbox, смотрите Поддерживаемые Распределения.
Можно задать объект вероятности для пользовательского дистрибутива и затем использовать приложение Distribution Fitter или функции объекта вероятности, такие как pdf, cdf, icdf, и random, чтобы вычислять распределение, сгенерируйте случайные числа и так далее. Для получения дополнительной информации смотрите Задать Пользовательские дистрибутивы Используя Приложение Distribution Fitter. Можно также задать пользовательский дистрибутив с помощью указателя на функцию и использовать mle функционируйте, чтобы найти оценки наибольшего правдоподобия. Для примера сочтите целесообразным Пользовательский дистрибутив к Подвергнутым цензуре Данным.
Объекты вероятностного распределения позволяют вам строить распределение вероятности к выборочным данным или задавать распределение настройкой значений параметров. Можно затем выполнить множество исследований объекта распределения.
Оцените параметры вероятностного распределения от выборочных данных путем подбора объекта распределения вероятностей к данным с помощью fitdist. Можно соответствовать одному заданному параметрическому или непараметрическому распределению к выборочным данным. Можно также соответствовать нескольким распределениям того же типа к выборочным данным на основе сгруппированных переменных. Для большинства распределений, fitdist оценка наибольшего правдоподобия (MLE) использования, чтобы оценить параметры распределения от выборочных данных. Для получения дополнительной информации и дополнительных опций синтаксиса, смотрите fitdist.
В качестве альтернативы можно создать объект вероятностного распределения с заданными значениями параметров с помощью makedist.
Если вы создаете объект вероятностного распределения, можно использовать объектные функции для:
Вычислите доверительные интервалы для параметров распределения (paramci).
Вычислите итоговую статистику, включая среднее значение (mean), медиана (median), межквартильный размах (iqr), отклонение (var), и стандартное отклонение (std).
Оцените функцию плотности вероятности (pdf).
Оцените кумулятивную функцию распределения (cdf) или обратная кумулятивная функция распределения (icdf).
Вычислите отрицательную логарифмическую правдоподобность (negloglik) и профилируйте функцию правдоподобия (proflik) для распределения.
Сгенерируйте случайные числа от распределения (random).
Обрежьте распределение до заданных нижних и верхних пределов (truncate).
Чтобы сохранить ваше вероятностное распределение возражают против.MAT файла:
На панели инструментов нажмите Save Workspace. Эта опция сохраняет все переменные в вашей рабочей области, включая любые объекты вероятностного распределения.
В браузере рабочей области щелкните правой кнопкой по вероятностному распределению, возражают и выбирают Save as. Эта опция сохраняет только выбранный объект вероятностного распределения, не другие переменные в вашей рабочей области.
В качестве альтернативы можно избавить объект вероятностного распределения непосредственно от командной строки при помощи save функция. save позволяет вам выбрать имя файла и указать, что вероятностное распределение возражает, что вы хотите сохранить. Если вы не задаете объект (или другая переменная), MATLAB® сохраняет все переменные в вашей рабочей области, включая любые объекты вероятностного распределения, к заданному имени файла. Для получения дополнительной информации и дополнительные опции синтаксиса, смотрите save.
В этом примере показано, как использовать объекты вероятностного распределения выполнить многоступенчатый анализ подходящего распределения.
Анализ иллюстрирует как к:
Стройте распределение вероятности к выборочным данным, которые содержат классы экзамена 120 студентов при помощи fitdist.
Вычислите среднее значение классов экзамена при помощи mean.
Постройте гистограмму данных о классе экзамена, наложенных с графиком PDF подходящего распределения, при помощи plot и pdf.
Вычислите контур для лучших 10 процентов студенческих классов при помощи icdf.
Сохраните подходящий объект вероятностного распределения при помощи save.
Загрузите выборочные данные.
load examgradesВыборочные данные содержат 120 5 матрица классов экзамена. Экзамены выиграны по шкале от 0 до 100.
Создайте вектор, содержащий первый столбец данных о классе экзамена.
x = grades(:,1);
Соответствуйте нормальному распределению к выборочным данным при помощи fitdist создать объект вероятностного распределения.
pd = fitdist(x,'Normal')pd =
NormalDistribution
Normal distribution
mu = 75.0083 [73.4321, 76.5846]
sigma = 8.7202 [7.7391, 9.98843]
fitdist возвращает объект вероятностного распределения, pd, из типа NormalDistribution. Этот объект содержит предполагаемые значения параметров, mu и sigma, для подходящего нормального распределения. Интервалы рядом с оценками параметра составляют 95% доверительных интервалов для параметров распределения.
Вычислите среднее значение классов экзамена студентов с помощью подходящего объекта распределения, pd.
m = mean(pd)
m = 75.0083
Среднее значение классов экзамена равно mu параметр оценивается fitdist.
Постройте гистограмму классов экзамена. Наложите график подходящего PDF визуально сравнить подходящее нормальное распределение с фактическими классами экзамена.
x_pdf = [1:0.1:100]; y = pdf(pd,x_pdf); figure histogram(x,'Normalization','pdf') line(x_pdf,y)

PDF подходящего распределения следует за той же формой как гистограмма классов экзамена.
Определите контур для верхних 10 процентов студенческих классов экзамена при помощи обратной кумулятивной функции распределения (icdf). Этот контур эквивалентен значению, в котором cdf вероятностного распределения равен 0,9. Другими словами, 90 процентов классов экзамена меньше чем или равны граничному значению.
A = icdf(pd,0.9)
A = 86.1837
На основе подходящего распределения 10 процентов студентов получили оценку экзамена, больше, чем 86,1837. Эквивалентно, 90 процентов студентов получили оценку экзамена, меньше чем или равную 86,1837.
Сохраните строившее распределение вероятности, pd, как файл с именем myobject.mat.
save('myobject.mat','pd')
Можно также работать с вероятностными распределениями с помощью специфичных для распределения функций. Эти функции полезны для генерации случайных чисел, вычислительной итоговой статистики в цикле или скрипте и передаче cdf или PDF как указатель на функцию (MATLAB) к другой функции. Можно также использовать эти функции, чтобы выполнить расчеты на массивах значений параметров, а не одном наборе параметров. Для списка поддерживаемых вероятностных распределений смотрите Поддерживаемые Распределения.
В этом примере показано, как использовать специфичные для распределения функции, чтобы выполнить многоступенчатый анализ подходящего распределения.
Анализ иллюстрирует как к:
Стройте распределение вероятности к выборочным данным, которые содержат классы экзамена 120 студентов при помощи normfit.
Постройте гистограмму данных о классе экзамена, наложенных с графиком PDF подходящего распределения, при помощи plot и normpdf.
Вычислите контур для лучших 10 процентов студенческих классов при помощи norminv.
Сохраните предполагаемые параметры распределения при помощи save.
Можно выполнить тот же анализ с помощью объекта вероятностного распределения. Смотрите Анализируют Распределение Используя Объекты Распределения вероятностей.
Загрузите выборочные данные.
load examgradesВыборочные данные содержат 120 5 матрица классов экзамена. Экзамены выиграны по шкале от 0 до 100.
Создайте вектор, содержащий первый столбец данных о классе экзамена.
x = grades(:,1);
Соответствуйте нормальному распределению к выборочным данным при помощи normfit.
[mu,sigma,muCI,sigmaCI] = normfit(x)
mu = 75.0083
sigma = 8.7202
muCI = 2×1
73.4321
76.5846
sigmaCI = 2×1
7.7391
9.9884
normfit функция возвращает оценки параметров нормального распределения и 95% доверительных интервалов для оценок параметра.
Постройте гистограмму классов экзамена. Наложите график подходящего PDF визуально сравнить подходящее нормальное распределение с фактическими классами экзамена.
x_pdf = [1:0.1:100]; y = normpdf(x_pdf,mu,sigma); figure histogram(x,'Normalization','pdf') line(x_pdf,y)

PDF подходящего распределения следует за той же формой как гистограмма классов экзамена.
Определите контур для верхних 10 процентов студенческих классов экзамена при помощи нормальной обратной кумулятивной функции распределения. Этот контур эквивалентен значению, в котором cdf вероятностного распределения равен 0,9. Другими словами, 90 процентов классов экзамена меньше чем или равны граничному значению.
A = norminv(0.9,mu,sigma)
A = 86.1837
На основе подходящего распределения 10 процентов студентов получили оценку экзамена, больше, чем 86,1837. Эквивалентно, 90 процентов студентов получили оценку экзамена, меньше чем или равную 86,1837.
Сохраните предполагаемые параметры распределения как файл с именем myparameter.mat.
save('myparameter.mat','mu','sigma')
В этом примере показано, как использовать функцию распределения вероятностей normcdf как указатель на функцию в тесте качества подгонки хи-квадрата (chi2gof).
Этот пример тестирует нулевую гипотезу, которую выборочные данные содержали во входном векторе, x, прибывает из нормального распределения параметрами µ и σ, равный среднему значению (mean) и стандартное отклонение (std) из выборочных данных, соответственно.
rng('default') % For reproducibility x = normrnd(50,5,100,1); h = chi2gof(x,'cdf',{@normcdf,mean(x),std(x)})
h = 0
Возвращенный результат h = 0 указывает на тот chi2gof не отклоняет нулевую гипотезу на 5%-м уровне значения по умолчанию.
Этот следующий пример иллюстрирует, как использовать функции распределения вероятностей в качестве указателя на функцию в сэмплере среза (slicesample). Пример использует normpdf сгенерировать случайную выборку 2 000 значений от стандартного нормального распределения и графики гистограмма получившихся значений.
rng('default') % For reproducibility x = slicesample(1,2000,'pdf',@normpdf,'thin',5,'burnin',1000); histogram(x)

Гистограмма показывает это, при использовании normpdf, получившаяся случайная выборка имеет стандартное нормальное распределение.
Если вы передаете функцию распределения вероятностей для экспоненциального распределения PDF (exppdf) как указатель на функцию вместо normpdf, затем slicesample генерирует эти 2 000 случайных выборок от экспоненциального распределения со значением параметров по умолчанию µ, равного 1.
rng('default') % For reproducibility x = slicesample(1,2000,'pdf',@exppdf,'thin',5,'burnin',1000); histogram(x)

Гистограмма показывает что получившаяся случайная выборка при использовании exppdf имеет экспоненциальное распределение.
Приложения и пользовательские интерфейсы обеспечивают интерактивный подход к работе с параметрическими и непараметрическими вероятностными распределениями.
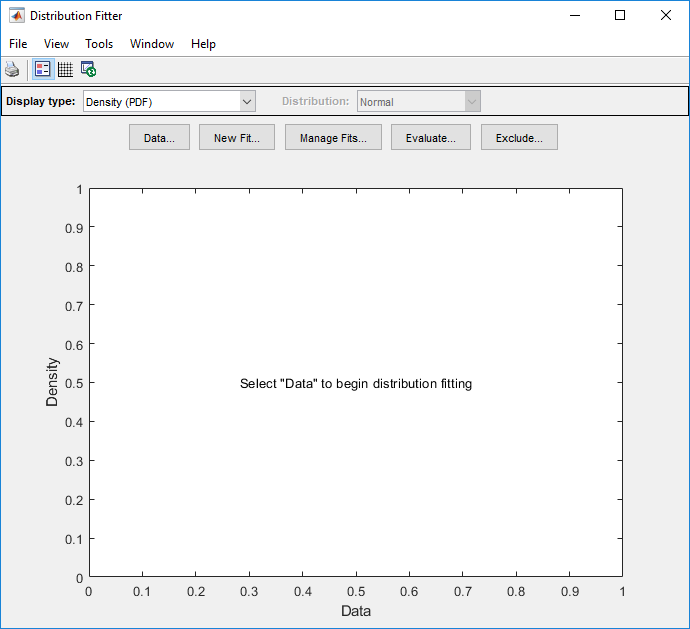
Приложение Distribution Fitter позволяет вам в интерактивном режиме строить распределение вероятности к своим данным. Можно отобразить различные типы графиков, вычислить доверительные границы и оценить припадок данных. Можно также исключить данные из подгонки. Можно сохранить данные и экспортировать подгонку к рабочей области как объект вероятностного распределения выполнить последующий анализ.
Загрузите приложение Distribution Fitter от вкладки Apps, или путем ввода distributionFitter в Командном окне. Для получения дополнительной информации смотрите, что Данные модели Используют Приложение Distribution Fitter.
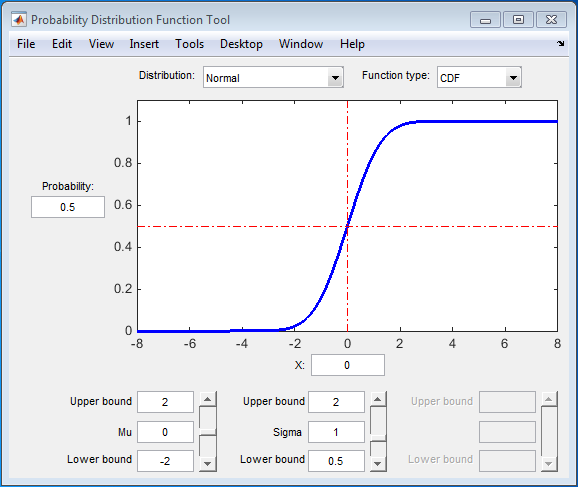
Пользовательский интерфейс Probability Distribution Function визуально исследует вероятностные распределения. Можно загрузить пользовательский интерфейс Probability Distribution Function путем ввода disttool в Командном окне.
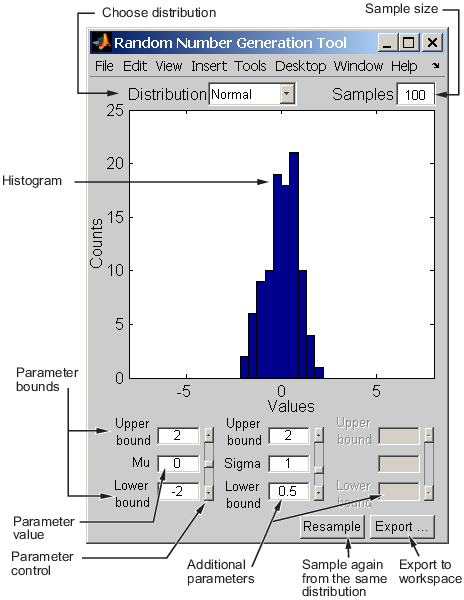
Пользовательский интерфейс Генерации случайных чисел генерирует случайные данные из заданного распределения и экспортирует результаты в вашу рабочую область. Можно использовать этот инструмент, чтобы исследовать эффекты изменяющихся параметров и объема выборки на распределениях.
Пользовательский интерфейс Генерации случайных чисел позволяет вам устанавливать значения параметров для распределения и изменять их нижние и верхние границы; чертите другую выборку от того же распределения, с помощью того же размера и параметров; и экспортируйте текущую случайную выборку в свою рабочую область для использования в последующем анализе. Диалоговое окно позволяет вам обеспечить имя для выборки.
Distribution Fitter | Probability Distribution Function | fitdist | makedist | randtool