Фазовая модуляция

Фазовая модуляция является линейным методом полосовой модуляции, в котором сообщение модулирует фазу постоянного амплитудного сигнала. Communications Toolbox™ обеспечивает модуляторы и демодуляторы для этих методов фазовой модуляции:

Манипулирование сдвига фазы (PSK) — Двоичный файл, квадратура и общий PSK
Дифференциальное манипулирование сдвига фазы (DPSK) — Двоичный файл, квадратура и общий DPSK
Возместите QPSK (OQPSK)

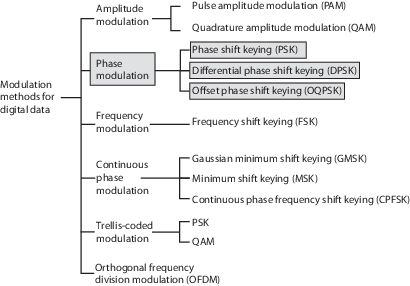
Чтобы модулировать входные данные с этими методами, можно использовать функции MATLAB^®, Системные объекты или блоки Simulink^®.

Схема модуляции	Функции MATLAB	Системные объекты	Блоки Simulink
Бинарный PSK (BPSK)		`comm.BPSKModulator` `comm.BPSKDemodulator`	BPSK Modulator Baseband BPSK Demodulator Baseband
Квадратурный PSK (QPSK)		`comm.QPSKModulator` `comm.QPSKDemodulator`	QPSK Modulator Baseband QPSK Demodulator Baseband
Общий PSK	`pskmod` `pskdemod`	`comm.PSKModulator` `comm.PSKDemodulator`	M-PSK Modulator Baseband M-PSK Demodulator Baseband
Дифференциальный BPSK (DBPSK)		`comm.DBPSKModulator` `comm.DBPSKDemodulator`	DBPSK Modulator Baseband DBPSK Demodulator Baseband
Дифференциальный QPSK (DQPSK)		`comm.DQPSKModulator` `comm.DQPSKDemodulator`	DQPSK Modulator Baseband DQPSK Demodulator Baseband
Общий DPSK	`dpskmod` `dpskdemod`	`comm.DPSKModulator` `comm.DPSKDemodulator`	M-DPSK Modulator Baseband M-DPSK Demodulator Baseband
OQPSK		`comm.OQPSKModulator` `comm.OQPSKDemodulator`	OQPSK Modulator Baseband OQPSK Demodulator Baseband

Основная полоса и симуляция полосы пропускания

Communications Toolbox поддерживает основную полосу и методы симуляции полосы пропускания; однако, сдвиг фазы, включающий методы, поддерживает основополосную симуляцию только.

Общая форма волны полосы пропускания может быть представлена как

$Y_{1} (t) \cos (2 π f_{c} t + θ) - Y_{2} (t) \sin (2 π f_{c} t + θ),$

где _fc является несущей частотой, и θ является начальной фазой сигнала поставщика услуг. Это уравнение равно действительной части

$[(Y_{1} (t) + j Y_{2} (t)) e^{j θ}] \exp (j 2 π f_{c} t) .$

В основополосной симуляции только моделируется выражение в квадратных скобках. Векторный y является выборкой комплексного сигнала

$(Y_{1} (t) + j Y_{2} (t)) e^{j θ} .$

BPSK

В бинарном манипулировании сдвига фазы (BPSK) фаза постоянного амплитудного сигнала переключается между двумя значениями, соответствующими двоичному файлу 1 и двоичному файлу 0. Форма волны полосы пропускания сигнала BPSK

$s_{n} (t) = \sqrt{\frac{2 E_{b}}{T_{b}}} \cos (2 π f_{c} t + π (1 - n)); n \in {0, 1},$

где:

_Eb является энергией на бит.
_Tb является битной длительностью.
_fc является несущей частотой.

В MATLAB основополосное представление сигнала BPSK

$s_{n} (t) = \cos (π n); n \in {0, 1} .$

Сигнал BPSK имеет две фазы: 0 и π.

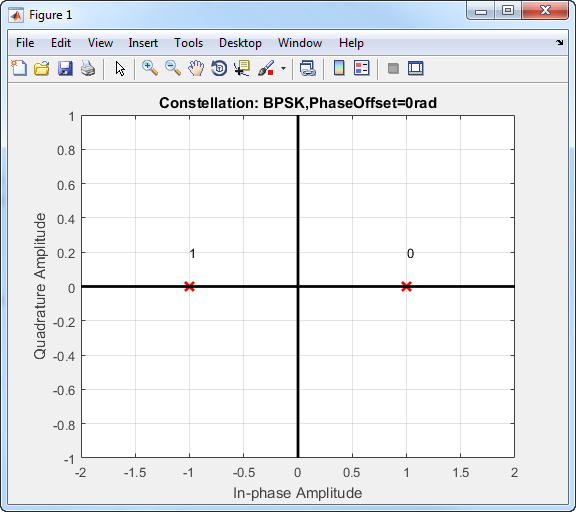
Вероятность небольшой ошибки в канале AWGN

$P_{b} = Q (\sqrt{\frac{2 E_{b}}{N_{0}}}),$

где _N0 является шумовой степенью спектральная плотность.

QPSK

В квадратурном манипулировании сдвига фазы биты сообщения сгруппированы в 2-битные символы, которые передаются как одна из четырех фаз постоянного амплитудного сгенерированного модулированного сигнала. Эта группировка обеспечивает КПД пропускной способности, который является вдвое более большим, чем КПД BPSK. Общий сигнал QPSK описывается как

$s_{n} (t) = \sqrt{\frac{2 E_{s}}{T_{s}}} \cos (2 π f_{c} t + (2 n + 1) \frac{π}{4}); n \in {0, 1, 2, 3},$

где _Es является энергией на символ, и _Ts является длительностью символа. Комплексное основополосное представление сигнала QPSK

$s_{n} (t) = \exp (j π (\frac{2 n + 1}{4})); n \in {0, 1, 2, 3} .$

В этой схеме созвездия QPSK каждая 2-битная последовательность сопоставлена с одним из четырех возможных состояний. Состояния соответствуют фазам π/4, 3π/4, 5π/4, и 7π/4.

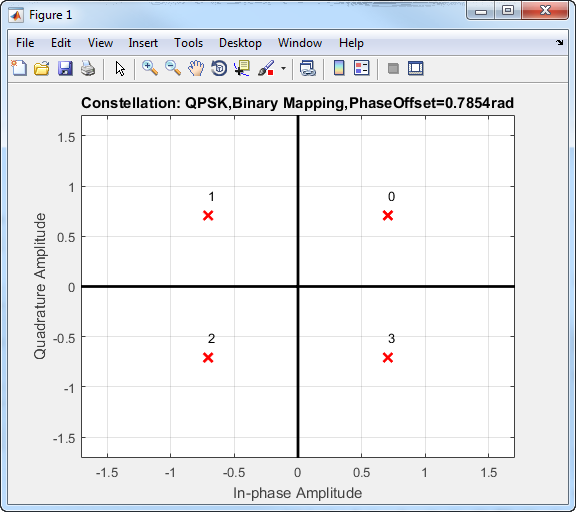
Чтобы улучшать производительность частоты ошибок по битам, входящие биты могут быть сопоставлены с серо-закодированным упорядоченным расположением.

Двоичное-к-серому отображение

Двоичная последовательность	Серо-закодированная последовательность
00	00
01	01
10	11
11	10

Первичное преимущество Кода Грея состоит в том, что только одно из изменений на два бита при перемещении между смежным созвездием указывает. Коды Грея могут быть применены к модуляциям высшего порядка, как показано в этом серо-закодированном созвездии QPSK.

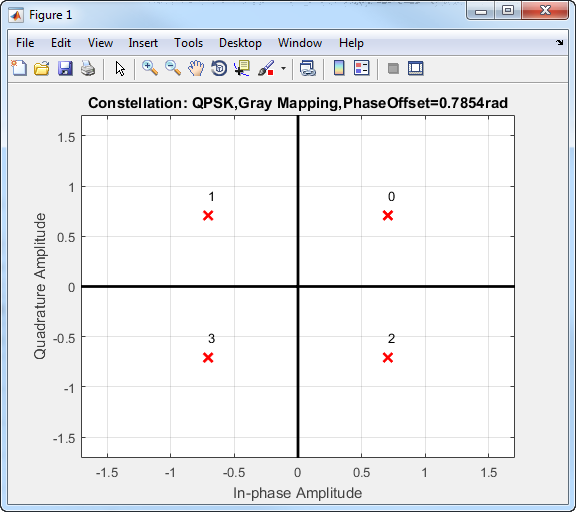
Вероятность битовой ошибки для QPSK в AWGN с Серым кодированием

$P_{b} = Q (\sqrt{\frac{2 E_{b}}{N_{0}}}),$

который совпадает с выражением для BPSK. В результате QPSK предоставляет той же эффективности дважды КПД пропускной способности.

PSK высшего порядка

В MATLAB можно модулировать и демодулировать созвездия PSK высшего порядка. Комплексная основополосная форма для M-арного сигнала PSK использование естественного упорядоченного двоичному файлу отображения символа

$s_{n} (t) = \exp (j π (\frac{2 n + 1}{M})); n \in {0, 1, \dots, M - 1} .$

Это созвездие 8-PSK использует серо-закодированное отображение символа.

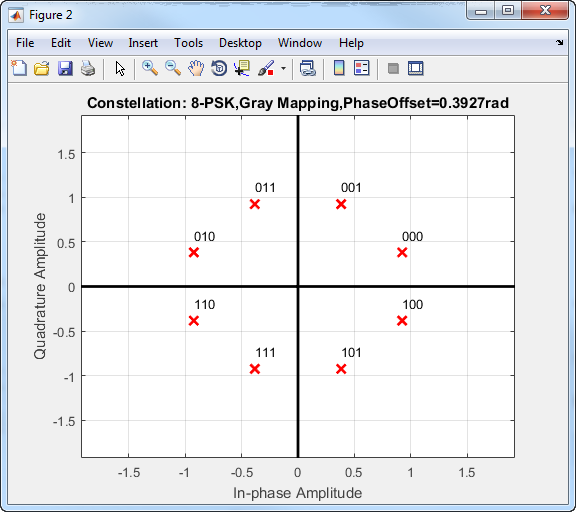
Для порядков модуляции вне 4, ухудшается эффективность частоты ошибок по битам PSK в AWGN. В следующем рисунке QPSK и кривые BPSK перекрывают друг друга.

DPSK

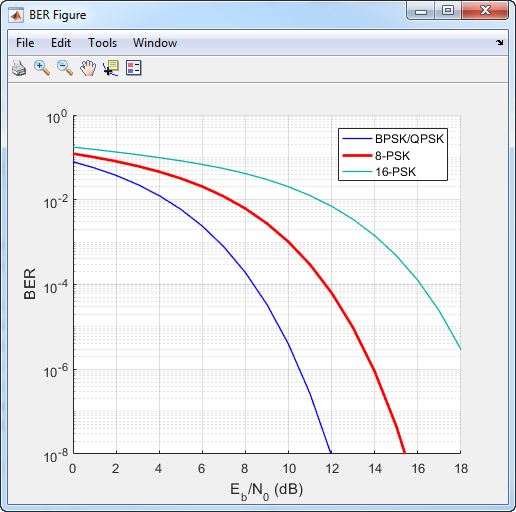
DPSK является некогерентной формой сдвига фазы, вводящего, который не требует когерентного опорного сигнала в приемнике. С DPSK различие между последовательными вводимыми символами сопоставлено с определенной фазой. Как пример, для бинарного DPSK (DBPSK), схема модуляции действует таким образом, что различие между последовательными битами сопоставлено с двоичным файлом 0 или 1. Когда входной бит равняется 1, дифференцированно закодированный символ остается то же самое как предыдущий символ, в то время как поступление 0 переключателей выходной символ.

Недостаток DPSK - то, что это - приблизительно 3 дБ, менее энергосберегающие, чем когерентный PSK. Вероятностью битовой ошибки для DBPSK в AWGN является _Pb = 1/2 exp (_Eb/_N0).

OQPSK

QPSK смещения похож на QPSK за исключением того, что выравнивание времени синфазных потоков битов и квадратурных потоков битов отличается. В QPSK, синфазном и квадратурном переходе потоков битов одновременно. В OQPSK переходы имеют смещение периода полусимвола как показано.

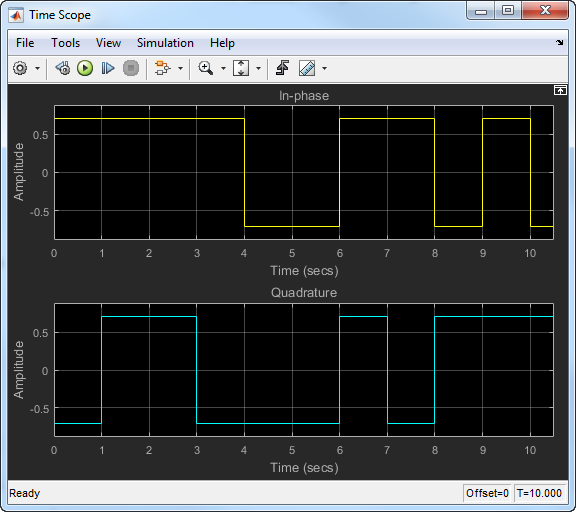
Синфазное и квадратура сигнализируют о переходе только на контурах между символами. Эти переходы происходят в 1 втором интервале, потому что частота дискретизации составляет 1 Гц. Следующий рисунок показывает синфазные сигналы и квадратурные сигналы для сигнала OQPSK.

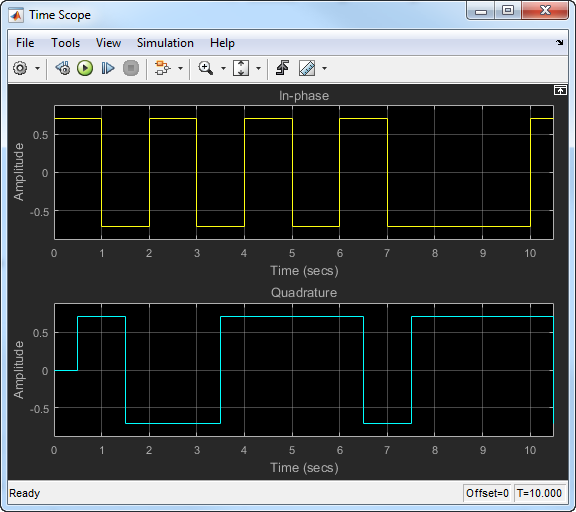
Для OQPSK квадратурный сигнал имеет 1/2 смещение периода символа (0,5 с).

BER для сигнала OQPSK в AWGN идентичен тому из сигнала QPSK. BER

$P_{b} = Q (\sqrt{\frac{2 E_{b}}{N_{0}}}),$

где _Eb является энергией на бит, и _N0 является шумовой степенью спектральная плотность.

Демодуляция мягкого решения

Все функции демодулятора Communications Toolbox, Системные объекты и блоки могут демодулировать двоичные данные с помощью или трудных решений или мягких решений. Два мягких алгоритма выбора решения доступны: точное отношение логарифмической правдоподобности (LLR) и аппроксимированный LLR. Точный LLR обеспечивает самую большую точность, но медленнее, в то время как аппроксимированный, LLR менее точен, но более эффективен.

Точный алгоритм LLR

Отношение логарифмической правдоподобности (LLR) является логарифмом отношения вероятностей 0 битов, передаваемых по сравнению с 1 битом, передаваемым для полученного сигнала. LLR некоторое время, b, задан как:

$L (b) = \log (\frac{\Pr (b = 0 | r = (x, y))}{\Pr (b = 1 | r = (x, y))})$

Принимая равную вероятность для всех символов, LLR для канала AWGN может быть описан как:

$L (b) = \log (\frac{\sum_{s \in S_{0}} e^{- \frac{1}{σ^{2}} ({(x - s_{x})}^{2} + {(y - s_{y})}^{2})}}{\sum_{s \in S_{1}} e^{- \frac{1}{σ^{2}} ({(x - s_{x})}^{2} + {(y - s_{y})}^{2})}})$

Переменная	Описание
$r$	Полученный сигнал с координатами (x, y)
$b$	Переданный бит (один из битов K в M-арном символе, принимая все символы M одинаково вероятны),
$S_{0}$	Идеальные символы или созвездие указывают с битом 0 в данной позиции двоичного разряда
$S_{1}$	Идеальные символы или созвездие указывают с битом 1 в данной позиции двоичного разряда
$s_{x}$	Синфазная координата идеального символа или точки созвездия
$s_{y}$	Квадратурная координата идеального символа или точки созвездия
$σ^{2}$	Шумовое отклонение сгенерированного модулированного сигнала
$σ_{x}^{2}$	Шумовое отклонение вдоль синфазной оси
$σ_{y}^{2}$	Шумовое отклонение вдоль квадратурной оси

Примечание

Шумовые компоненты вдоль синфазных осей и квадратурных осей приняты, чтобы быть независимыми и равной степени, то есть, $σ_{x}^{2} = σ_{y}^{2} = σ^{2} / 2$ .

Аппроксимируйте алгоритм LLR

Аппроксимированный LLR вычисляется только при помощи самой близкой точки созвездия к полученному сигналу с 0 (или 1) в той позиции двоичного разряда, а не всех точках созвездия, как сделано в точном LLR. Это задано в [2] как:

$L (b) = - \frac{1}{σ^{2}} (\min_{s \in S_{0}} ({(x - s_{x})}^{2} + {(y - s_{y})}^{2}) - \min_{s \in S_{1}} ({(x - s_{x})}^{2} + {(y - s_{y})}^{2}))$

Ссылки

[1] Rappaport, Радиосвязи Теодора С.: Принципы и Практика. Верхний Сэддл-Ривер, NJ: Prentice Hall, 1996, стр 238–248.

[2] Viterbi, A. J. “Интуитивное Выравнивание и Упрощенное внедрение Декодера MAP для Сверточных кодов”, Журнал IEEE на Выбранных областях в Коммуникациях. Издание 16, № 2, февраль 1998, стр 260–264

Документация