Communications Toolbox™ обеспечивает источники, приемники и дисплеи, которые упрощают анализ эффективности системы связи.
Используйте функции и блоки, перечисленные в Источниках и Приемниках, чтобы сгенерировать случайные данные, чтобы симулировать источник сигнала.
Случайные символы
randsrc функция генерирует случайные матрицы, записи которых выбраны независимо из алфавита, который вы задаете с распределением, которое вы задаете. Особый случай генерирует биполярные матрицы.
Например, команда ниже генерирует 5 4 матрица, записи которой случайны, независимо выбранные и равномерно распределены в наборе {1,3,5}.
a = randsrc(5,4,[1,3,5])
a = 5×4
5 1 1 1
5 1 5 3
1 3 5 5
5 5 3 5
3 5 5 5
Чтобы скосить распределение так, чтобы 1 было вдвое более вероятно произойти, чем или 3 или 5, используйте команду ниже. Третий входной параметр имеет две строки, одна из которых указывает на возможные значения b и другой указывает на вероятность каждого значения.
b = randsrc(5,4,[1,3,5; .5,.25,.25])
b = 5×4
3 5 3 5
1 3 1 3
5 1 1 1
5 3 1 5
3 1 1 1
Случайные целые числа
В MATLAB®, randi функция генерирует случайные целочисленные матрицы, записи которых находятся в диапазоне, который вы указываете. Особый случай генерирует случайные бинарные матрицы.
Например, команда ниже генерирует 5 4 матрица, содержащая случайные целые числа между 2 и 10.
c = randi([2,10],5,4)
c = 5×4
5 6 4 6
5 6 8 10
8 7 7 5
9 8 3 7
3 8 3 4
Если ваша желаемая область значений [0,10] вместо [2,10], можно использовать любую из команд ниже. Они приводят к различным числовым результатам, но используют то же распределение.
d = randi([0,10],5,4); e = randi([0 10],5,4);
В Simulink® блокируется Случайный Целочисленный Целочисленный Генератор Генератора и Пуассона, оба генерируют векторы, содержащие случайные неотрицательные целые числа. Блок Random Integer Generator использует равномерное распределение на ограниченном диапазоне, который вы указываете в маске блока. Блок Poisson Integer Generator использует распределение Пуассона, чтобы определить его выход. В частности, выход может включать любое неотрицательное целое число.
Случайные шаблоны битовой ошибки
В MATLAB, randerr функция генерирует матрицы, записи которых или 0 или 1. Однако его опции отличаются от тех из randi, потому что randerr предназначается для тестирования кодирования контроля ошибок. Например, команда ниже генерирует 5 4 бинарную матрицу, где каждая строка содержит точно один 1.
f = randerr(5,4)
f = 5×4
0 0 0 1
1 0 0 0
1 0 0 0
0 0 1 0
0 0 0 1
Вы можете использовать такую команду, чтобы встревожить двоичный код, который состоит из пяти четырехбитных кодовых комбинаций. Добавление случайного матричного f к вашей матрице кода (по модулю 2) вводит точно одну ошибку в каждую кодовую комбинацию.
С другой стороны, чтобы встревожить каждую кодовую комбинацию путем начинания одной ошибки с вероятности 0,4 и две ошибки с вероятностью 0.6, используйте команду ниже вместо этого. Каждая строка имеет один '1' с вероятностью 0.4, в противном случае два '1's
g = randerr(5,4,[1,2; 0.4,0.6])
g = 5×4
1 0 1 0
0 1 0 1
0 0 0 1
1 0 0 1
0 0 1 0
Добавление случайного матричного g к вашей матрице кода (по модулю 2) вводит одну или две ошибки в каждую кодовую комбинацию с заданной вероятностью вхождения для каждого. Матрица вероятности, которая является третьим аргументом randerr влияет только на номер 1 с в каждой строке, не их размещение.
Как другое приложение, можно сгенерировать равновероятный бинарный вектор-столбец с 100 элементами с помощью любой из команд ниже. Эти три команды производят различные числовые выходные параметры, но используют то же распределение. Третьи входные параметры варьируются согласно конкретному способу каждой функции задать его поведение.
binarymatrix1 = randsrc(100,1,[0 1]); % Possible values are 0,1 binarymatrix2 = randi([0 1],100,1); % Two possible values binarymatrix3 = randerr(100,1,[0 1; 0.5 0.5]); % No 1s, or one 1
В Simulink блок Bernoulli Binary Generator генерирует случайные биты и подходит для представления источников. Блок рассматривает каждый элемент сигнала быть независимой Бернуллиевой случайной переменной. Кроме того, различные элементы не должны быть тождественно распределены.
Создайте шумовые блоки генератора в Simulink®, чтобы симулировать линии связи.
Можно создать случайные шумовые генераторы, чтобы симулировать шум канала при помощи блока MATLAB Function (Simulink) с производящими функциями случайных чисел. Создайте различные типы шума канала при помощи следующих комбинаций.
| Распределение | Блок | Функция |
|---|---|---|
| Гауссов | MATLAB Function (Simulink) | wgn |
| Рэлеевский | MATLAB Function (Simulink) | randn |
| Rician | MATLAB Function (Simulink) | randn |
| Универсальная форма на ограниченном интервале | MATLAB Function (Simulink) | rand |
Смотрите Случайные Шумовые Генераторы для примера того, как Рейли и распределенный шум Рикиэна создаются.
В MATLAB®, wgn функция генерирует случайные матрицы с помощью распределения белого Гауссова шума. Вы задаете степень шума в любом dBW (децибелы относительно ватта), dBm, или линейные модули. Можно сгенерировать или действительный или комплексный шум.
Например, команда ниже генерирует вектор-столбец длины 50 содержащий действительный белый Гауссов шум, степень которого является 2 dBW. По умолчанию тип степени в dBW и импедансе загрузки составляет 1 Ом.
y1 = wgn(50,1,2);
Сгенерировать комплексный белый Гауссов шум, степень которого составляет 2 ватта, через загрузку 60 Ом, использование любую из команд ниже.
y2 = wgn(50,1,2,60,'complex','linear'); y3 = wgn(50,1,2,60,'linear','complex');
Чтобы отправить сигнал через аддитивный канал белого Гауссова шума, используйте awgn функция. См. Канал AWGN для получения дополнительной информации.
Используйте функции, Системные объекты и блоки, перечисленные в Источниках и Приемниках, чтобы сгенерировать последовательности для распространения или синхронизации в системе связи. Можно сгенерировать псевдослучайные последовательности, коды синхронизации и ортогональные коды. Для примеров, сравнивающих свойства корреляции этих генераторов последовательности, смотрите Распространяющиеся Последовательности.
Можно сгенерировать псевдослучайный или псевдошум (PN) последовательности с помощью этих Системных объектов в MATLAB® и этих блоков в Simulink. Приложения этих последовательностей диапазон от нескольких-доступов распространяют системы связи спектра к расположению, синхронизации и шифрованию данных.
| Последовательность | Система object™ | Блок |
|---|---|---|
| Последовательности Голда | comm.GoldSequence | Gold Sequence Generator |
| Последовательности Kasami | comm.KasamiSequence | Kasami Sequence Generator |
| Псевдошумовые последовательности | comm.PNSequence | PN Sequence Generator |
Чтобы сгенерировать псевдослучайные последовательности, базовый код реализует сдвиговые регистры, как проиллюстрировано в этой схеме.
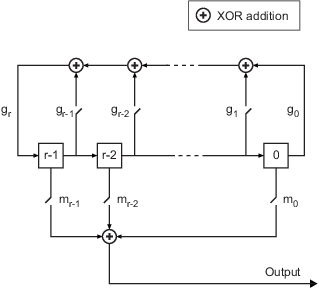
Все регистры r в генераторе обновляют свои значения на каждом временном шаге согласно значению входящей стрелы к сдвиговому регистру. Сумматоры выполняют сложение по модулю 2. Сдвиговый регистр может быть описан бинарным полиномом в z, g rzr + gr-1zr-1 +... + g 0. Содействующий g i 1 год, если существует связь, или 0, если нет никакой связи с ith сдвигового регистра на сумматор.
Содействующий m i 1 год, если существует задержка или 0, если нет никакой задержки с ith сдвигового регистра на сумматор, предшествующий выходу. Если сдвиг является нулем, переключатель m 0 закрывается, в то время как весь другой m k переключатели открыт.
Kasami и генераторы псевдошумовой последовательности используют это полиномиальное описание для их полинома генератора. Генератор последовательности Голда использует это полиномиальное описание для предпочтительных первых и вторых псевдошумовых последовательностей полинома генератора.
Этот пример показывает, что последовательности выводили от PN Sequence Generator может быть смоделирован с помощью линейного сдвигового регистра обратной связи (LFSR), созданного с примитивными блоками Simulink®.

Для выбранного полинома генератора, p (z) =z^6+z+1, модель генерирует псевдошумовую последовательность периода 63, при помощи PN Sequence Generator блокируйтесь и путем моделирования LFSR использование примитивных блоков Simulink. Эти два параметра, Initial states и Output mask vector (or scalar shift value), интерпретированы в схематичной модели LFSR. PreLoadFcn функция обратного вызова используется, чтобы инициализировать параметры периода выполнения. Чтобы просмотреть функции обратного вызова, перейдите к MODELING> SETUP> Model Settings> Model Properties, и выберите Callbacks вкладка.
Выход scope показывает, что эти две реализации производят соответствие с псевдошумовыми последовательностями.

Используя PN Sequence Generator блок позволяет вам легко генерировать псевдошумовые последовательности больших периодов. Чтобы экспериментировать далее, откройте модель. Измените настройки, чтобы видеть, как эффективность варьируется для различных задержек пути, или настройте параметры генератора псевдошумовой последовательности. Можно экспериментировать с различными начальными состояниями путем изменения значения начальных состояний до выполнения симуляции. Для всех значений две сгенерированных последовательности являются тем же самым.
Используйте comm.BarkerCode Системный объект и блок Barker Code Generator, чтобы сгенерировать коды Баркера, чтобы выполнить синхронизацию. Коды Баркера являются подмножествами псевдошумовых последовательностей. Они - короткие коды с длиной самое большее 13, которые являются боковыми лепестками низкой корреляции. Боковой лепесток корреляции является корреляцией кодовой комбинации с переключенной временем версией себя.
Ортогональные коды используются для распространения, чтобы извлечь выгоду из их совершенных свойств корреляции. Когда используется в многопользовательских системах спектра распространения, где приемник отлично синхронизируется с передатчиком, despreading операция идеальна.
| Код | Системный объект | Блок |
|---|---|---|
| Адамар кодирует | comm.HadamardCode | Hadamard Code Generator |
| Коды OVSF | comm.OVSFCode | OVSF Code Generator |
| Уолш кодирует | comm.WalshCode | Walsh Code Generator |
Библиотека блоков Приемников Коммуникации содержит осциллографы для просмотра трех типов графиков сигнала:
В следующей таблице перечислены блоки и графики, которые они генерируют.
| Имя блока | Plots |
|---|---|
| Eye Diagram Scope | Глазковая диаграмма для сигнала |
| Constellation Diagram | Схема созвездия и траектория сигнала сигнала |
Глазковая диаграмма является простым и удобным инструментом для изучения эффектов интерференции межсимвола и других нарушений канала в цифровой передаче. Когда этот программный продукт создает глазковую диаграмму, он строит полученный сигнал против времени на оси фиксированного интервала. В конце фиксированного интервала это повторяется к началу оси времени. В результате схема состоит из многих перекрывающихся кривых. Один способ использовать глазковую диаграмму состоит в том, чтобы искать место, где глаз наиболее широко открыт, и используйте ту точку в качестве момента принятия решения когда demapping демодулируемый сигнал восстановить цифровое сообщение.
Блок Eye Diagram Scope производит глазковые диаграммы. Это дискретное время процессов блока сигналы и периодически чертит линию, чтобы указать на решение, согласно параметру маски.
Примеры появляются в поле зрения Синусоида и Представление Модулируемый Сигнал.
Схема созвездия сигнала строит значение сигнала в своих моментах принятия решения. В лучшем случае моменты принятия решения должны быть время от времени, когда глаз глазковой диаграммы сигнала наиболее широко открыт.
Блок Constellation Diagram производит схему созвездия из сигналов дискретного времени. Пример появляется в поле зрения Синусоида.
Траектория сигнала является непрерывным графиком сигнала в зависимости от времени. Траектория сигнала отличается от графика рассеивания, в котором последние отображения указывает на траектории сигнала на дискретные интервалы времени.
Блок Constellation Diagram производит траектории сигнала. Блок Constellation Diagram производит траектории сигнала когда ShowTrajectory свойство установлено в истину. Траектория сигнала соединяет все точки входного сигнала, независимо от заданного фактора децимации (Samples per symbol)
Следующая модель производит схему созвездия и глазковую диаграмму от комплексного синусоидального сигнала. Поскольку интервал времени принятия решений почти, но не точно, целочисленное кратное период синусоиды, выставки глазковой диаграммы дрейфуют в зависимости от времени. А именно, последовательные трассировки в глазковой диаграмме и последовательные точки на точечной диаграмме находятся друг около друга, но не перекрываются.
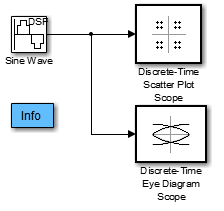
Чтобы открыть модель, введите doc_eyediagram в командной строке MATLAB. Чтобы создать модель, соберите и сконфигурируйте эти блоки:
Sine Wave, в библиотеке Sources DSP System Toolbox™ (не блок Sine Wave в библиотеке Simulink Sources)
Установите Frequency на .502.
Установите Output complexity на Complex.
Установите Sample time на 1/16.
Constellation Diagram, в библиотеке Comm Sinks
На панели Constellation Properties, набор Samples per symbol к 16.
Eye Diagram Scope, в библиотеке Comm Sinks
На панели Plotting Properties, набор Samples per symbol к 16.
На панели Figure Properties, набор Scope position к figposition([42.5 55 35 35]);.
Соедините блоки как показано на предыдущем рисунке. В разделе Simulate, набор Stop time к 250. Раздел Simulate появляется на нескольких вкладках. Выполнение модели производит следующий график точечной диаграммы.
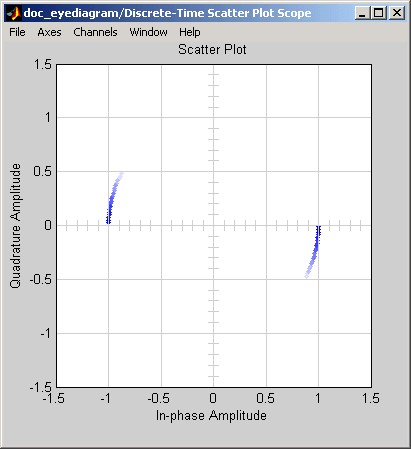
Точки графика рассеивания лежат на круге радиуса 1. Обратите внимание на то, что точки исчезают как передачи времени. Это вызвано тем, что флажок рядом с Color fading устанавливается под Rendering Properties, который заставляет осциллограф представлять точки более смутно больше времени, которое передает после того, как они построены. Если вы очищаете это поле, вы видите полный круг точек.
Блок Constellation Diagram отображает круговую траекторию.
В глазковой диаграмме верхний набор трассировок представляет действительную часть сигнала, и более низкий набор трассировок представляет мнимую часть сигнала.
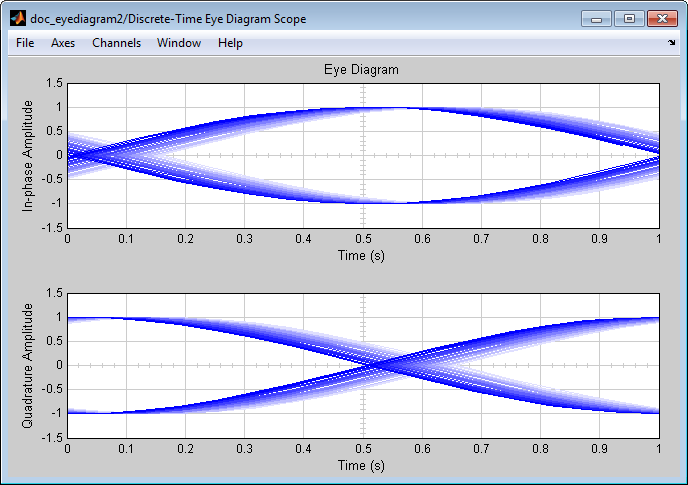
Этот многослойный пример создает глазковую диаграмму, график рассеивания и график траектории сигнала для модулируемого сигнала. Это исследует графики один за другим в этих разделах:
Следующая модель модулирует случайный сигнал с помощью QPSK, фильтрует сигнал с повышенным фильтром косинуса и создает глазковую диаграмму из отфильтрованного сигнала.
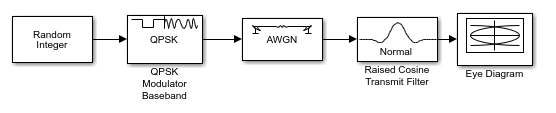
Чтобы открыть модель, введите doc_signaldisplays в командной строке MATLAB. Чтобы создать модель, соберите и сконфигурируйте следующие блоки:
Random Integer Generator, в подбиблиотеке Random Data Sources библиотеки Comm Sources
Установите M-ary number на 4.
Установите Sample time на 0.01.
QPSK Modulator Baseband, в PM в подбиблиотеке Digital Baseband библиотеки Modulation Communications Toolbox, параметрами по умолчанию
AWGN Channel, в библиотеке Channels Communications Toolbox, со следующими изменениями в установках параметров по умолчанию:
Установите Mode на Signal-to-noise ratio (SNR).
Установите SNR (dB) на 15.
Raised Cosine Transmit Filter, в библиотеке Comm Filters
Установите Filter shape на Normal.
Установите Rolloff factor на 0.5.
Установите Filter span in symbols на 6.
Установите Output samples per symbol на 8.
Установите Input processing на Elements as channels (sample based).
Eye Diagram Scope, в библиотеке Comm Sinks
Установите Samples per symbol на 8.
Установите Symbols per trace на 3. Это задает количество символов, которые отображены в каждой трассировке глазковой диаграммы. Трассировка является любой из отдельных линий в глазковой диаграмме.
Установите Traces displayed на 3.
Установите New traces per display на 1. Это задает количество новых трассировок, которые появляются каждый раз, когда схема обновляется. Количеством трассировок, которые остаются в схеме от одного обновления до следующего, является Traces displayed минус New traces per display.
На панели Rendering Properties, набор Markers к + указать на точки, построенные на каждой выборке. Значение по умолчанию Markers пусто, который не указывает ни на какой маркер.
На панели Figure Properties, набор Eye diagram to display к In-phase only.
Когда вы запускаете модель, Глазковая диаграмма отображает следующую схему. Ваше точное изображение варьируется в зависимости от того, когда вы приостанавливаете или останавливаете симуляцию.
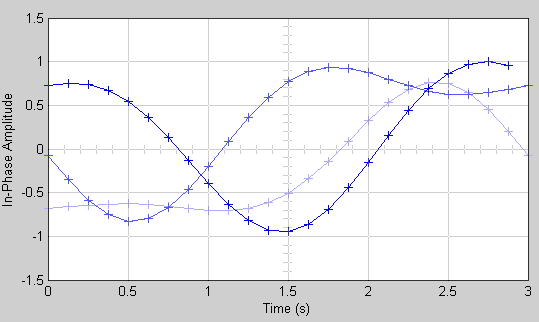
Отображены три трассировки. Трассировки 2 и 3 исчезаются, потому что Color fading под Rendering Properties выбран. Это заставляет трассировки быть отображенными менее ярко более старое, которое они. В этом изображении Трассировка 1 нова, и Трассировка 3 является самой старой. Поскольку New traces per display установлен в 1, только Трассировка 1 появляется впервые. Трассировки 2 и 3 также появляются в предыдущем отображении.
Поскольку Symbols per trace установлен в 3, каждая трассировка содержит три символа, и потому что Samples per trace установлен в 8, каждый символ содержит восемь выборок. Обратите внимание на то, что проследите 1, содержит 24 точки, который является продуктом Symbols per trace и Samples per symbol. Однако трассировки 2 и 3 содержат 25 точек каждый. Последняя точка в трассировке 2, на правильной границе осциллографа, представляет ту же выборку как первая точка в трассировке 1 на левой границе осциллографа. Точно так же последняя точка в трассировке 3 представляет ту же выборку как первая точка в трассировке 2. Эти дублирующиеся точки указывают, где трассировки встретились бы, если бы они были отображены рядом друг с другом, как проиллюстрировано в следующем изображении.
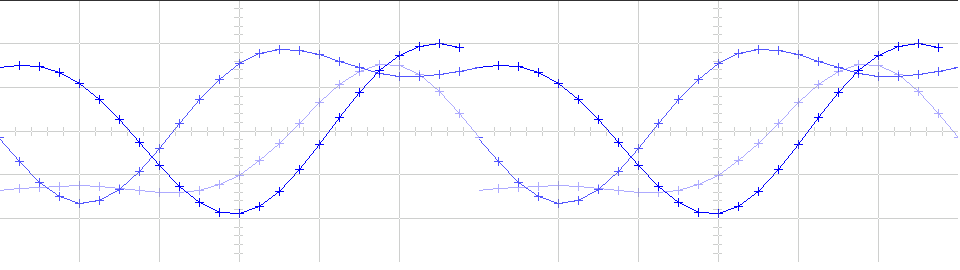
Можно просмотреть более реалистическую глазковую диаграмму путем изменения значения Traces displayed к 40 и очистка поля Markers .
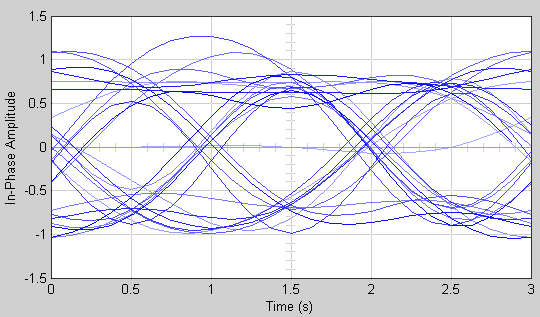
Когда параметр Offset устанавливается на 0, графический вывод запускается в центре первого символа, так, чтобы открытая часть глазковой диаграммы была посреди графика для большинства точек.
Следующая модель создает график рассеивания того же сигнала, рассмотренного в Глазковой диаграмме для Модулируемого Сигнала.

Чтобы создать модель, следуйте инструкциям в Глазковой диаграмме для Модулируемого Сигнала, но замените блок Eye Diagram на следующий блок:
Constellation Diagram, в Communications Toolbox / библиотека Comm Sinks
Установите Samples per symbol на 2
Установите Offset на 0. Это задает количество выборок, чтобы пропустить прежде, чем построить первую точку.
Установите Symbols to display на 40.
Когда вы запускаете симуляцию, блок Constellation Diagram отображает следующий график.
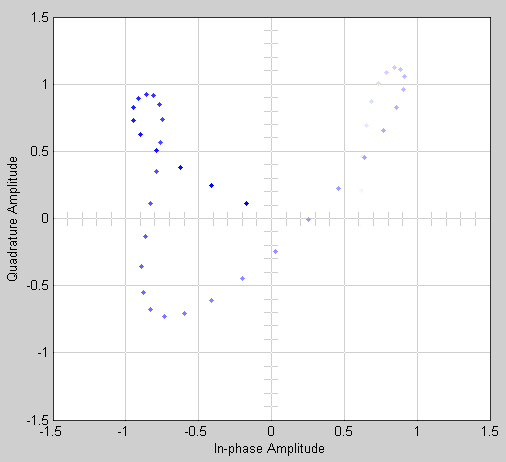
График отображает 30 точек. Поскольку Color fading под Rendering Properties выбран, точки отображены менее ярко более старое, которое они.
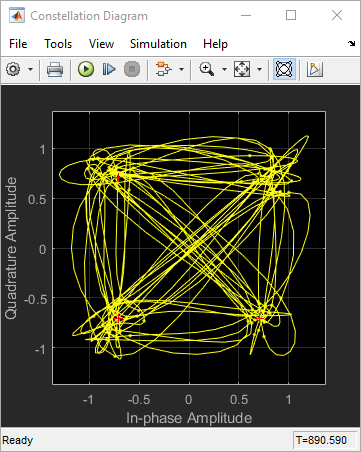
Следующая модель создает график траектории сигнала того же сигнала, рассмотренного в Глазковой диаграмме для Модулируемого Сигнала.
Чтобы создать модель, следуйте инструкциям в Глазковой диаграмме для Модулируемого Сигнала, но замените блок Eye Diagram на следующий блок:
Constellation Diagram , в Communications Toolbox / библиотека Comm Sinks
Установите Samples per symbol на 8.
Установите Symbols to display на 40. Это задает количество символов, отображенных в траектории сигнала. Общее количество отображенных точек является продуктом Samples per symbol и Symbols to display.
Когда вы запускаете модель, Схема Созвездия отображает траекторию как та ниже.
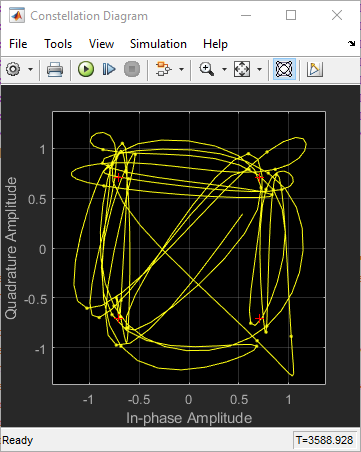
График отображает 40 символов. Поскольку Color fading под Rendering Properties выбран, символы отображены менее ярко более старое, которое они.
См. Схему Созвездия Модулируемого Сигнала сравнить предыдущую траекторию сигнала с графиком рассеивания того же сигнала. Блок Constellation Diagram соединяет точки, отображенные блоком Constellation Diagram, чтобы отобразить траекторию сигнала.
Если вы увеличиваете Symbols to display до 100, модель производит траекторию сигнала как та ниже. Общее количество точек, отображенных в любой момент, 800, который является продуктом параметров Samples per symbol и Symbols to display.