В этом примере показано, как использовать краткий arima(p,D,q) синтаксис, чтобы задать AR по умолчанию () модель,
По умолчанию все параметры в созданном объекте модели имеют неизвестные значения, и инновационное распределение является Гауссовым с постоянным отклонением.
Задайте модель AR (2) по умолчанию:
Mdl = arima(2,0,0)
Mdl =
arima with properties:
Description: "ARIMA(2,0,0) Model (Gaussian Distribution)"
Distribution: Name = "Gaussian"
P: 2
D: 0
Q: 0
Constant: NaN
AR: {NaN NaN} at lags [1 2]
SAR: {}
MA: {}
SMA: {}
Seasonality: 0
Beta: [1×0]
Variance: NaN
Выход показывает что созданный объект модели, Mdl, имеет NaN значения для всех параметров модели: постоянный термин, коэффициенты AR и отклонение. Можно изменить созданный объект модели с помощью записи через точку или ввести его (наряду с данными) к estimate.
В этом примере показано, как задать AR (p) модель с постоянным равным нулю термином. Используйте синтаксис значения имени, чтобы задать модель, которая отличается от модели по умолчанию.
Задайте модель AR (2) без постоянного термина,
где инновационное распределение является Гауссовым с постоянным отклонением.
Mdl = arima('ARLags',1:2,'Constant',0)
Mdl =
arima with properties:
Description: "ARIMA(2,0,0) Model (Gaussian Distribution)"
Distribution: Name = "Gaussian"
P: 2
D: 0
Q: 0
Constant: 0
AR: {NaN NaN} at lags [1 2]
SAR: {}
MA: {}
SMA: {}
Seasonality: 0
Beta: [1×0]
Variance: NaN
ARLags аргумент значения имени задает задержки, соответствующие ненулевым коэффициентам AR. Свойство Constant в созданном объекте модели равно 0, как задано. Объект модели имеет значения по умолчанию для всех других свойств, включая NaN значения как заполнители для неизвестных параметров: коэффициенты AR и скалярное отклонение.
Можно изменить созданный объект модели с помощью записи через точку или ввести его (наряду с данными) к estimate.
В этом примере показано, как задать AR (p) модель с ненулевыми коэффициентами в непоследовательных задержках.
Задайте модель AR (4) с ненулевыми коэффициентами AR в задержках 1 и 4 (и никакой постоянный термин),
где инновационное распределение является Гауссовым с постоянным отклонением.
Mdl = arima('ARLags',[1,4],'Constant',0)
Mdl =
arima with properties:
Description: "ARIMA(4,0,0) Model (Gaussian Distribution)"
Distribution: Name = "Gaussian"
P: 4
D: 0
Q: 0
Constant: 0
AR: {NaN NaN} at lags [1 4]
SAR: {}
MA: {}
SMA: {}
Seasonality: 0
Beta: [1×0]
Variance: NaN
Выход показывает ненулевые коэффициенты AR в задержках 1 и 4, как задано. Свойство P равно 4, количество преддемонстрационных наблюдений должно было инициализировать модель AR. Неограниченные параметры равны NaN.
Отобразите значение AR:
Mdl.AR
ans=1×4 cell array
{[NaN]} {[0]} {[0]} {[NaN]}
AR массив ячеек возвращает четыре элемента. Первые и последние элементы (соответствующий задержкам 1 и 4) имеют значение NaN, указание на эти коэффициенты является ненулевым и должно быть оценено или в противном случае задано пользователем. arima устанавливает коэффициенты во временных задержках, равных нулю обеспечивать непротиворечивость с индексацией массива ячеек MATLAB®.
В этом примере показано, как задать ARMA (p, q) модель с известными значениями параметров. Можно использовать такую полностью заданную модель в качестве входа к simulate или forecast.
Задайте модель ARMA(1,1)
где инновационное распределение является t Студента с 8 степенями свободы и постоянным отклонением 0.15.
tdist = struct('Name','t','DoF',8); Mdl = arima('Constant',0.3,'AR',0.7,'MA',0.4,... 'Distribution',tdist,'Variance',0.15)
Mdl =
arima with properties:
Description: "ARIMA(1,0,1) Model (t Distribution)"
Distribution: Name = "t", DoF = 8
P: 1
D: 0
Q: 1
Constant: 0.3
AR: {0.7} at lag [1]
SAR: {}
MA: {0.4} at lag [1]
SMA: {}
Seasonality: 0
Beta: [1×0]
Variance: 0.15
Все значения параметров заданы, то есть, никаким свойством объекта не является NaN- ценный.
В этом примере показано, как задать AR () модель с t инновационным распределением Студента.
Задайте модель AR (2) без постоянного термина,
где инновации следуют за t распределением Студента с неизвестными степенями свободы.
Mdl = arima('Constant',0,'ARLags',1:2,'Distribution','t')
Mdl =
arima with properties:
Description: "ARIMA(2,0,0) Model (t Distribution)"
Distribution: Name = "t", DoF = NaN
P: 2
D: 0
Q: 0
Constant: 0
AR: {NaN NaN} at lags [1 2]
SAR: {}
MA: {}
SMA: {}
Seasonality: 0
Beta: [1×0]
Variance: NaN
Значение Distribution struct массив с полем Name равняйтесь 't' и поле DoF равняйтесь NaN. NaN значение указывает, что степени свободы неизвестны, и должны быть оценены с помощью estimate или в противном случае заданный пользователем.
В приложении Econometric Modeler можно задать структуру задержки, присутствие константы, и инновационное распределение модели AR (p) путем выполнения этих шагов. Все заданные коэффициенты являются неизвестными, допускающими оценку параметрами.
В командной строке откройте приложение Econometric Modeler.
econometricModeler
В качестве альтернативы откройте приложение из галереи Apps (см. Econometric Modeler).
В Data Browser выберите ряд времени отклика, к которому модель будет подходящей.
На вкладке Econometric Modeler, в разделе Models, нажимают AR.
Диалоговое окно AR Model Parameters появляется.
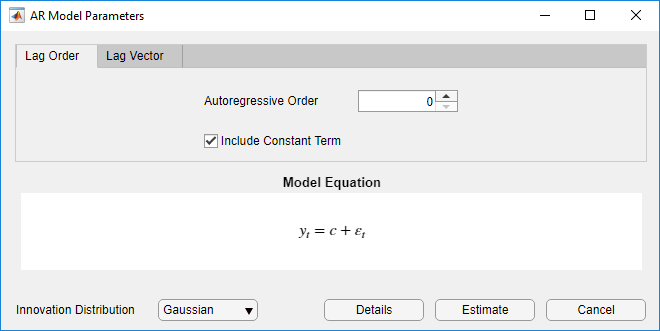
Задайте структуру задержки. Чтобы задать модель AR (p), которая включает все задержки AR от 1 до p, используйте вкладку Lag Order. Для гибкости, чтобы задать включение особых задержек, используйте вкладку Lag Vector. Для получения дополнительной информации смотрите Полиномы Оператора Задержки Определения В интерактивном режиме. Независимо от вкладки вы используете, можно проверить форму модели путем осмотра уравнения в разделе Model Equation .
Например:
Задавать модель AR (2), которая включает константу, включает первую задержку и имеет Гауссово инновационное распределение, установите Autoregressive Order на 2.
Задавать модель AR (2), которая включает первую задержку, имеет Распределение Гаусса, но не включает константу:
Установите Autoregressive Order на 2.
Снимите флажок Include Constant Term.
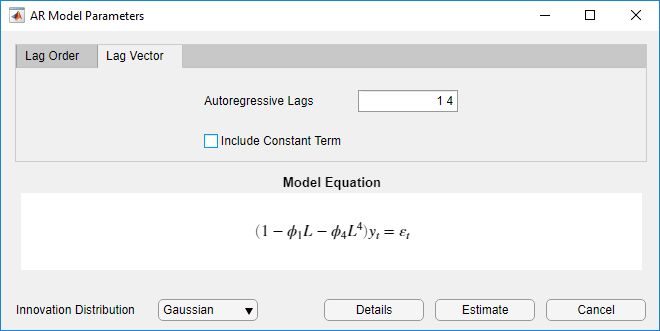
Задавать модель AR (4), содержащую непоследовательные задержки
где εt является серией Гауссовых инноваций IID:
Кликните по вкладке Lag Vector.
Установите Autoregressive Lags на 1 4.
Снимите флажок Include Constant Term.
Задавать модель AR (2), которая включает первую задержку, включает постоянный термин и имеет t - распределенные инновации:
Установите Autoregressive Lags на 2.
Нажмите кнопку Innovation Distribution, затем выберите t.
Параметр степеней свободы распределения t является неизвестным, но допускающим оценку параметром.
После того, как вы зададите модель, нажмите Estimate, чтобы оценить все неизвестные параметры в модели.