Получите находящиеся на диске поля от размера диска и скоса
umargin и diskmargin усиление модели и изменение фазы как мультипликативный факторный F (s), принимающий значения в диске, сосредоточенном на вещественной оси. Диск описан двумя параметрами: ɑ, который устанавливает размер изменения, и σ или скос, который смещает изменение усиления к увеличению или уменьшению. (Дополнительную информацию см. в Алгоритмах об этой модели.) Диск может альтернативно быть описан его прерываниями вещественной оси DGM = [gmin,gmax], которые представляют относительный объем изменения усиления вокруг номинальной стоимости F = 1. Использование gm2dm и dm2gm преобразовывать между ɑ, значениями σ и находящимся на диске запасом по амплитуде DGM = [gmin,gmax] это описывает тот же диск.
[ возвращает усиление и изменения фазы, смоделированные диском с размером диска GM,PM] = dm2gm(alpha)alpha и нулевой скос. Диск представляет усиление, которое может варьироваться между 1/GM и GM времена номинальная стоимость и фаза, которая может варьироваться ±PM степени. Если alpha вектор, функция возвращает GM и PM для каждой записи в векторе.
[ возвращает находящееся на диске изменение усиления DGM,DPM] = dm2gm(alpha,sigma)DGM и находящееся на диске изменение фазы DPM соответствие диску параметрируется alpha и sigma. DPM вектор из формы [gmin,gmax], и DPM вектор из формы [-pm,pm] соответствие размеру диска alpha и скошенный sigma. Если alpha и sigma векторы, затем функция возвращает области значений для пар alpha1,sigma1;...;alphaN,sigmaN.
Определите находящееся на диске усиление и изменения фазы, полученные диском с размером α = 0.5.
alpha = 0.5; [GM,PM] = dm2gm(alpha)
GM = 1.6667
PM = 28.0725
Когда вы не используете sigma, dm2gm команда возвращает усиление и изменения фазы, соответствующие α с нулевым скосом. Нулевой скос означает, что диск представляет усиление, которое может увеличиться или уменьшиться той же суммой. В этом случае, α = 0,5 модели усиление, которое может увеличиться или уменьшиться до фактора 1.6667 из его номинальной стоимости. Изменение фазы, соответствующее этому находящемуся на диске изменению усиления, составляет ±28 °. Визуализируйте этот диск.
diskmarginplot(alpha,0,'disk')
График показывает значения F в комплексной плоскости, соответствующей размеру диска alpha = 0.5 и sigma = 0. Вы видите тот DGM = [1/GM,GM] для этого диска.
Определите находящееся на диске усиление и изменения фазы, смоделированные диском, параметрированным размером диска α = 0.6, и скосите σ = 0.75.
alpha = 0.6; sigma = 0.75; [DGM,DPM] = dm2gm(alpha,sigma)
DGM = 1×2
0.6066 2.2632
DPM = 1×2
-34.2267 34.2267
Визуализируйте усиление и изменения фазы, представленные этим диском.
diskmarginplot(DGM)
Поскольку σ> 0, этот диск моделирует усиление, которое может увеличить больше, чем это может уменьшиться относительно номинальной стоимости.
Определите находящееся на диске усиление и изменения фазы, представленные дисками, одного размера, но с различными скосами.
alpha = 0.75; sigma = [-0.5;0;0.5]; [DGM,DPM] = dm2gm(alpha,sigma)
DGM = 3×2
0.3684 1.9231
0.4545 2.2000
0.5200 2.7143
DPM = 3×2
-41.7908 41.7908
-41.1121 41.1121
-41.7908 41.7908
Дисковое получение примерно подобные изменения фазы, но скос смещает диск к уменьшению усиления или увеличению. Для диска с нулевым скосом изменение усиления сбалансировано, и означая, что усиление может увеличиться или уменьшиться той же суммой. Визуализировать одновременную область значений усиления и изменений фазы, соответствующих каждой строке в DGM.
diskmarginplot(DGM)
umargin и diskmargin усиление модели и изменения фазы отдельной обратной связи образовывают канал как зависимый частотой мультипликативный фактор F (s) умножение номинального ответа разомкнутого контура L (s), такой, что встревоженным ответом является L (s) F (s). Факторный F (s) параметрируется:
В этой модели,
δ (s) является ограниченной усилением динамической неопределенностью, нормированной так, чтобы это всегда варьировалось в единичном диске (|| δ || ∞ <1).
ɑ устанавливает сумму усиления и изменения фазы, смоделированного F. Для фиксированного σ параметр ɑ управляет размером диска. Для ɑ = 0, мультипликативный фактор равняется 1, соответствуя номинальному L.
σ, названный skew, смещает смоделированную неопределенность к увеличению усиления или уменьшению усиления.
Факторный F принимает значения в диске, сосредоточенном на вещественной оси и содержащий номинальную стоимость F = 1. Диск характеризуется его прерыванием DGM = [gmin,gmax] с вещественной осью. gmin <1 и gmin > 1 минимальные и максимальные относительные изменения в усилении, смоделированном F, в номинальной фазе. Неопределенность фазы, смоделированная F, является областью значений DPM = [-pm,pm] из значений фазы в номинальном усилении (|F | = 1). Например, в следующем графике, правая сторона показывает диску F, который пересекает вещественную ось в интервале [0.71 1.4]. Левая сторона показывает, что этот диск моделирует изменение усиления ±3 дБ и изменение фазы ±19 °.
DGM = [0.71,1.4]
F = umargin('F',DGM)
plot(F)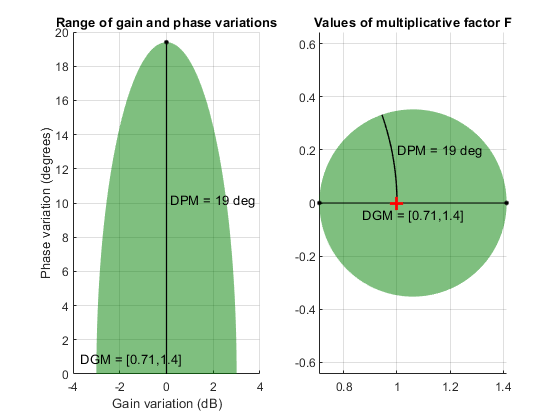
gm2dm и gm2dm преобразует между этими двумя способами задать диск мультипликативного усиления и неопределенности фазы: область значений изменения усиления формы DGM = [gmin,gmax], и ɑ, параметризация σ соответствующего диска.
Для получения дальнейшей информации о модели неопределенности для усиления и изменений фазы, смотрите, что Анализ Устойчивости Использует Дисковые Поля.
diskmargin | diskmarginplot | gm2dm | umargin | wcdiskmargin