Анализ устойчивости Используя дисковые поля

Дисковые поля определяют количество устойчивости системы с обратной связью против усиления или изменений фазы ответа разомкнутого контура. В находящихся на диске граничных вычислениях, модели ПО такие изменения как дискообразная мультипликативная неопределенность на передаточной функции разомкнутого контура. disk margin измеряется, сколько неопределенности цикл может терпеть прежде, чем идти нестабильный.

Та сумма неопределенности соответствует минимальным запасам по амплитуде и фазе. Находящийся на диске DGM запаса по амплитуде является суммой, которой усиление цикла может увеличиться или уменьшиться без потери устойчивости в абсолютных единицах. Находящийся на диске DPM запаса по фазе является суммой, которой фаза цикла может увеличиться или уменьшиться без потери устойчивости в градусах. Эти находящиеся на диске поля учитывают все частоты и взаимодействия цикла. Поэтому находящийся на диске граничный анализ обеспечивает более сильную гарантию устойчивости, чем классические запасы по амплитуде и фазе.

Robust Control Toolbox™ предоставляет инструменты:

Анализируйте устойчивость системы против изменений фазы и усиления. Использование diskmargin вычислить находящиеся на диске запасы по амплитуде и фазе обратной связи SISO и MIMO.
Усиление модели и неопределенность фазы. Используйте umargin блок системы управления, чтобы анализировать эффект усиления и неопределенности на производительности системы и устойчивости.

Моделирование изменений усиления и фазы

Скрипт Open Live Script

Оба umargin и diskmargin представляйте усиление и изменение фазы как мультипликативный комплексный фактор F (s), заменяя номинальный ответ разомкнутого контура L (s) с L (s) *F (s). Фактор F принимает значения в диске, который включает номинальную стоимость F = 1. Это мультипликативные факторные модели и усиление и изменения фазы. Например, следующий график показывает один такой диск в комплексной плоскости.

DGM = [0.6,1.7];
diskmarginplot(DGM,'disk')

Значения в этом диске охватывают относительные изменения только для усиления области значений DGM = [0.6 1.7], или ±4 дБ. Они также представляют абсолютные изменения только для фазы DPM = [–29,29], или ±29 °. Полагайте, что следующая система с обратной связью, с номинальным циклом передают модульная обратная связь и L.

Если эта обратная связь остается устойчивой для всех значений F в диске, показанном в предыдущем графике, то находящимся на диске запасом по амплитуде L является, по крайней мере, DGM, и находящимся на диске запасом по фазе является, по крайней мере, DPM.

И umargin и diskmargin усиление модели и неопределенность фазы с семейством дисков, описанных двумя параметрами, α и σ. Для систем SISO диск параметрируется:

$F = \frac{1 + α [(1 - σ) / 2] δ}{1 - α [(1 + σ) / 2] δ} .$

В этой модели,

δ нормированная неопределенность (произвольное комплексное число на единичном диске | δ | <1).
α устанавливает сумму усиления и изменения фазы, смоделированного F. Для фиксированного σ параметр α управляет размером диска. Для α = 0, мультипликативный фактор равняется 1, соответствуя номиналу L.
σ, названный скосом, смещает смоделированную неопределенность к увеличению усиления или уменьшению усиления.

Каждый α,σ пара соответствует диску, который моделирует конкретную область значений изменения усиления DGM = [gmin, gmax], данный точками, где диск прерывает действительное (x) ось. Соответствующее изменение фазы DPM определяется углом между вещественной осью и линией через начало координат и касательную к диску. Таким образом можно описать смоделированный набор усиления и изменений фазы полностью или этими двумя значениями α,σ или этими двумя значениями DGM = [gmin, gmax]. σ = 0 моделирует сбалансированное изменение усиления с [gmin, gmax] таким образом что gmin = 1/gmax. Когда σ <0, затем F представляет большее уменьшение усиления, чем увеличение (gmin <1/gmax). С другой стороны σ> 0 представляет большее увеличение усиления, чем уменьшение. Например, считайте диски параметрированными α = 0,5 и три различных скоса, σ = –2, 0, и 2.

diskmarginplot(0.5,[-2 0 2],'disk')

Каждый α,σ пара соответствует диску, который моделирует различную область значений изменения усиления DGM = [gmin, gmax]. Исследуйте изменения усиления, которые соответствуют каждому из этих трех дисков.

Ranges = dm2gm(0.5,[-2  0 2])

Ranges = 3×2

    0.3333    1.4000
    0.6000    1.6667
    0.7143    3.0000

diskmarginplot(Ranges)

Сбалансированный σ = 0 областей значений симметричен вокруг номинальной стоимости, позволяя усилению увеличиться или уменьшиться на коэффициент приблизительно 1,67. Отрицательное σ значение соответствует большему количеству уменьшения усиления, чем увеличение, в то время как положительный σ дает больше увеличения, чем уменьшение.

umargin блок системы управления использует эту модель, чтобы представлять усиление и неопределенность фазы в обратной связи, устанавливая α и σ от значений запаса по амплитуде и фазе, которые вы задаете, когда вы создаете блок. diskmargin команда использует эту модель, чтобы вычислить находящиеся на диске запасы по амплитуде и фазе, как обсуждено в следующем разделе.

Дисковые поля для циклов SISO

Скрипт Open Live Script

Поскольку цикл передает L и данный скос σ, diskmargin команда находит самый большой размер диска α в который система с обратной связью feedback(L*F,1) устойчиво для всех значений F. Это значение α называется дисковым полем. Находящийся на диске запас по амплитуде DGM и находящийся на диске запас по фазе DPM область значений усиления и изменений фазы, представленных соответствующим диском.

Например, вычислите дисковое поле, и сопоставил находящиеся на диске запасы по амплитуде и фазе для передаточной функции SISO, с помощью значения по умолчанию σ = 0.

sigma = 0;
L = tf(25,[1 10 10 10]);
DM = diskmargin(L,sigma);  
alpha = DM.DiskMargin

alpha = 0.4581

DGM = DM.GainMargin

DGM = 1×2

    0.6273    1.5942

DPM = DM.PhaseMargin

DPM = 1×2

  -25.8017   25.8017

Для этой системы сбалансированный (σ = 0) дисковое поле α является приблизительно 0,46. Соответствующий находящийся на диске запас по амплитуде DGM показывает, что система остается устойчивой для относительных изменений усиления между приблизительно 0,63 и 1.6, или для изменений фазы приблизительно ±26 градусов. Этот результат устанавливает устойчивость для всех значений F в диске:

diskmarginplot(DGM,'disk')

Запасы по амплитуде являются пересечением диска с вещественной осью. Запас по фазе является самым большим углом между вещественной осью и линией через касательную источника к диску.

Объединенные изменения усиления и фазы

Запасы по амплитуде DGM вы получаете из diskmargin не примите изменение фазы и запасы по фазе DPM не примите изменение усиления. На практике ваша система может испытать одновременное усиление и изменения фазы. diskmarginplot позволяет вам визуализировать области значений одновременного усиления и изменений фазы, которые может терпеть система.

diskmarginplot(DGM)

Теневая область показывает устойчивую область значений объединенного усиления и изменений фазы. Таким образом, например, без изменения фазы, система может терпеть полный спектр DGM из изменения усиления, приблизительно-4 дБ к 4 дБ. Если фазе позволяют варьироваться приблизительно ±17 градусами, допустимое изменение усиления спадает до области значений приблизительно-3 дБ к 3 дБ.

Дисковые поля и скос

Области значений, показанные выше, вычисленные для σ = 0, представляют сбалансированное изменение усиления, где gmin = 1/gmax. Варьируясь скос может показать, более ли чувствителен цикл, чтобы получить увеличение или уменьшение. Например, использование σ> 0 может показать, что обратная связь очень устойчива, чтобы получить увеличение, потому что положительные σ модели больше увеличения усиления, чем уменьшение. Этот результат, однако, говорит мало о робастности, чтобы получить уменьшение. Попытайтесь вычислить находящиеся на диске запасы по амплитуде и фазе для L, сместив поля к увеличению усиления или получите уменьшение.

DMdec = diskmargin(L,-2);
DMinc = diskmargin(L,2); 
DGMdec = DMdec.GainMargin

DGMdec = 1×2

    0.4013    1.3745

DGMinc = DMinc.GainMargin

DGMinc = 1×2

    0.7717    1.7247

Соедините, эти результаты показывают, что в отсутствие изменения фазы, устойчивость обеспечена для относительных изменений усиления между 0,4 и 1.72. Чтобы видеть, как запас по фазе зависит от этих изменений усиления, постройте устойчивые области значений усиления и изменений фазы для каждого diskmargin результат.

diskmarginplot([DGMdec;DGM;DGMinc])
legend('\sigma = -2','\sigma = 0','\sigma = 2')
title('Stable range of gain and phase variations')

Этот график показывает, что обратная связь может терпеть большие изменения фазы, когда усиление уменьшается. Другими словами, устойчивость цикла более чувствительна, чтобы получить увеличение. Обратите внимание на то, что было бы ошибочно только брать самый большой запас по фазе, о котором сообщают (почти 30 градусов для σ = –2). Действительно, это большое значение утверждено на маленьком увеличении усиления меньше чем 3 дБ. И начиная с усиление и начиная с фаза подвергаются неопределенности в целом, важно обратить внимание на объединенные изменения. Например, график показывает это, когда увеличения усиления на 4 дБ, запас по фазе спадает меньше чем до 15 градусов. В отличие от этого, остается больше, чем 30 градусов, когда усиление уменьшается на 4 дБ.

В заключение варьируясь скос σ может дать более полное изображение чувствительности к неопределенности фазы и усилению. Если вы в основном не обеспокоены изменениями усиления одного направления (увеличение или уменьшение), не рекомендуется сделать выводы из одного ненулевого значения σ. Вместо этого используйте значение по умолчанию σ = 0, чтобы получить объективные оценки запасов по амплитуде и фазе. При использовании ненулевых значений σ используйте и положительные и отрицательные величины, чтобы сравнить относительную чувствительность, чтобы получить увеличение по сравнению с уменьшением усиления.

Диск неопределенности в плоскости Найквиста

Требование устойчивой устойчивости для системы с обратной связью feedback(L*F,1) эквивалентно требованию что 1 + L*F ≠ 0. В плоскости Найквиста это требование становится L (jω) ≠ –1/F. Таким образом диск F для каждого значения σ задает область исключения, которую не вводит кривая Найквиста, если устойчивость с обратной связью сохраняется. Все такие диски –1/F содержат критическую точку (–1,0) и являются касательной к кривой Найквиста. Скос настраивает размер и положение дисков касательной, как проиллюстрировано в следующем графике, который показывает области исключения для трех дисковых полей L, вычисленного выше. Как σ увеличения, каждый диск обеспечивает более низкие оценки классических запасов по амплитуде и фазе.

nyquist(L)
hold on
diskmarginplot([DGMdec;DGM;DGMinc],'nyquist')
p = findobj(gca,'type','patch');
legend(p,'\sigma = -2','\sigma = 0','\sigma = 2')
hold off

Для получения дополнительной информации об интерпретации Найквиста диска неопределенности, смотрите Дисковое Поле и Самое маленькое Возмущение Дестабилизации.

Модель неопределенности MIMO и дисковые поля обратной связи MIMO

Для систем MIMO модель применяет независимый диск неопределенности _Fj к каждому каналу цикла, данному

$F_{j} = \frac{1 + α [(1 - σ) / 2] δ_{j}}{1 - α [(1 + σ) / 2] δ_{j}} .$

Модель заменяет ответ разомкнутого контура MIMO L на L *F, где

$F = (\begin{matrix} F_{1} & 0 & 0 \\ 0 & ⋱ & 0 \\ 0 & 0 & F_{N} \end{matrix}) .$

Аналогичный случаю SISO, дисковое поле является самым большим значением α для который система с обратной связью feedback(L*F,eye(N)) устойчиво для всех значений F. Может быть полезно рассмотреть независимые изменения через все каналы обратной связи целиком, а также изменения отдельных каналов. Поэтому diskmargin позволяет вам вычислить:

Поля Loop-at-a-time — Максимальные терпимые изменения усиления (или изменения фазы) в каждом канале обратной связи, вычисленном со всеми другими замкнутыми кругами. Цикл за один раз анализ эффективно устанавливает весь _δj на 0 для всех каналов кроме канала при анализе.
Multiloop margins — Максимальные терпимые изменения усиления (или изменения фазы) через все каналы обратной связи. Многоконтурные поля допускают независимые изменения всех каналов обратной связи одновременно. Способность получить такие взаимодействия цикла является главным преимуществом граничного диском подхода по классическому граничному анализу. Многоконтурный анализ обычно дает к меньшим полям, чем цикл за один раз анализ.

Например, рассмотрите систему MIMO с 2 каналами следующего рисунка.

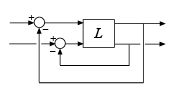
Для этой системы можно вычислить:

Максимальные терпимые изменения усиления (или изменения фазы) в первом канале (первый системный вход к первой системе выход)
Максимальные терпимые изменения усиления (или изменения фазы) во втором канале (второй системный вход к второй системе выход)
Максимальные терпимые независимые изменения усиления (или изменения фазы) в обоих каналах одновременно.

Для получения дополнительной информации и примеры того, как получить их, циклично выполняются за один раз и многоконтурные поля, видят diskmargin.

Изменения во входе объекта или объекте Выход

В некоторых случаях запасы устойчивости могут варьироваться в зависимости от того, применяются ли усиление и изменения фазы во входе объекта или объекте выход. diskmargin позволяет вам вычислить поля для изменений во входе, вывести, или оба одновременно. В общем случае поля для одновременных изменений ввода и вывода меньше, чем те для ввода или вывода только и обеспечивают более консервативную гарантию устойчивости. Считайте SISO или MIMO системой с обратной связью следующей схемы.

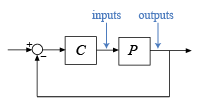
Можно вычислить дисковые поля при вводах и выводах объекта можно следующим образом.

[DM,MM] = diskmargin(P*C) возвращает поля для изменений на объекте выходные параметры.
[DM,MM] = diskmargin(C*P) возвращает поля для изменений во входных параметрах объекта.
MMIO = diskmargin(P,C) возвращает поле для одновременных изменений на объекте выходные параметры и входные параметры. При сравнении этого поля с полями в любом вводы или выводы используйте 2*MMIO.Diskmargin, с учетом одновременных возмущений, примененных при обоих вводах и выводах.

Зависимость частоты полей

В общем случае запасы по амплитуде и фазе варьируются через частоту. Это изменение происходит из-за изменения частоты ответа разомкнутого контура L: Для каждой частоты ω существует различный самый большой α (ω), таким образом, что I + L (jω) F является обратимым для всех значений F в диске. Этим значением является первый α (ω), для которого полюс с обратной связью пересекает ось jω на частоте ω, становясь нестабильным.

В то время как дисковое поле α варьируется через частоту, также - соответствующая терпимая область значений изменений фазы или усиления. При графическом выводе этих находящихся на диске полей, когда функция частоты предоставляет информацию о диапазонах частот со слабыми полями.

L = tf(25,[1 10 10 10]);
diskmarginplot(L)

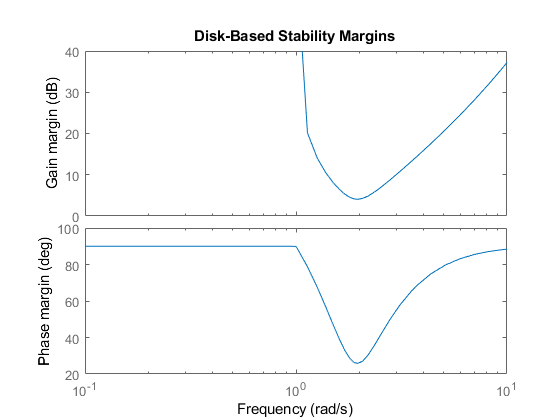
Disk margin plot showing disk-based gain and phase margins as a function of frequency

Дисковые поля, возвращенные diskmargin минимум такие значения по всем частотам. Щелкните правой кнопкой по графику, сгенерированному diskmarginplot для всплывающей подсказки с информацией об этих значениях.

Дисковые поля худшего случая

Дисковое поле вычисляется путем применения неопределенности к номинальной передаче цикла L и вычисление, как большой, что неопределенность может быть при сохранении устойчивости с обратной связью. Если передача цикла, L является самостоятельно неопределенной системой, то дисковое поле также варьируется как функция другой неопределенности в системе. worst-case disk margin является самым маленьким дисковым полем, которое происходит в областях значений неопределенности, смоделированной в L. Это - также минимальное гарантируемое поле в области значений неопределенности.

Вычислите дисковые поля худшего случая неопределенного системного использования wcdiskmargin. Эта функция оценивает дисковые поля худшего случая и соответствующие запасы по амплитуде и фазе худшего случая и для цикла за один раз и для многоконтурных изменений. Функция также возвращает возмущение худшего случая, комбинацию неопределенных элементов в L, который дает к самым слабым полям. Можно визуализировать худший случай находящиеся на диске поля с wcdiskmarginplot.

Дисковые поля и настройка системы управления

Настройка с `systune` или Control System Tuner

Настраивающие инструменты системы управления в Control System Toolbox™ позволяют вам задать целевые циклы for запасов по амплитуде и фазе в своей настроенной системе. Настраивающиеся цели TuningGoal.Margins (для командной строки, настраивающейся с systune) и Цель Полей (для настройки с Control System Tuner) использует находящиеся на диске поля. Таким образом, когда вы задаете независимые запасы по амплитуде и фазе GM и PM для настройки, программное обеспечение выбирает самый маленький α, который осуществляет оба значения. Этим α дают:

$α = \max [\frac{G M - 1}{G M + 1}, \tan (P M / 2)] .$

В применении этого значения α настраивающееся программное обеспечение принимает σ = 0.

Визуализация граничного использования целей viewGoal или графики настраивающей цели Control System Tuner эквивалентны diskmarginplot(L), где L настроенный ответ разомкнутого контура.

Устойчивый проект с `musyn`

Когда вы выполняете устойчивый контроллер, настраивающийся с musyn, можно смоделировать усиление и изменения фазы непосредственно системного использования umargin. Затем выполняя устойчивое проектирование контроллера с musyn осуществляет устойчивую устойчивость для смоделированной области значений изменений фазы и усиления. Этот подход полезен, потому что он позволяет вам изучать эффекты ожидаемого усиления и изменений фазы на всех аспектах производительности системы с помощью той же модели, которую вы используете для настройки. Для примера смотрите Устойчивый Контроллер для Вращения Спутника.

Недостаток этого подхода - это musyn не только осуществляет устойчивую устойчивость в целой смоделированной области значений неопределенности. Это также пытается осуществить устойчивую эффективность. (См. Устойчивый Критерий качества работы для Mu-Synthesis.) Достигающий этого более строгого требования обычно невозможно или приводит к невыносимому ухудшению номинальной эффективности. Таким образом вы можете должны быть уменьшать смоделированное усиление и изменения фазы, чтобы обеспечить разумную эффективность. systune и Control System Tuner не имеет этого недостатка, потому что они обрабатывают граничные цели независимо от любых целей эффективности.

Ссылки

[1] Загубите, Джеймс Д., Р. Лейн Дэйли и Дэгфинн Гэнгсаас. “Практический Проект Закона о надзоре для Самолета Используя Многомерные Методы”. Международный журнал Управления 59, № 1 (январь 1994): 93–137. https://doi.org/10.1080/00207179408923071.

[2] Seiler, Питер, Эндрю Пэкард и Паскаль Гахине. "Введение в Дисковые Поля". (Предстоящий) Журнал Систем управления IEEE. https://arxiv.org/abs/2003.04771.

Документация