Преобразуйте усиление и изменение фазы в находящееся на диске изменение усиления
В дисковом анализе поля усиление и изменения фазы моделируются как факторный F (s), умножающий ответ разомкнутого контура L (s). Этот фактор принимает значения в диске, D, сосредоточенный на вещественной оси с вещественной осью, прерывает gmin и gmax. Дисковое поле определяет самый большой размер диска [gmin,gmax] для которого обратная связь остается устойчивой. Это обеспечивает запас по амплитуде, по крайней мере, DGM = [gmin,gmax] и также некоторый запас по фазе DPM определенный дисковой геометрией.
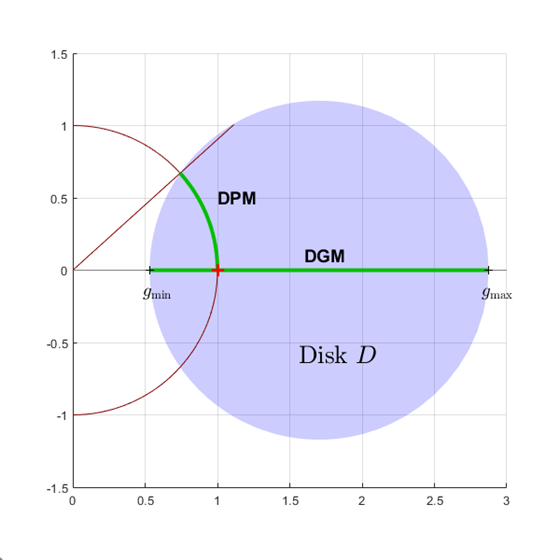
С другой стороны, getDGM берет желаемые запасы по амплитуде и фазе GM и PM и вычисляет самый маленький диск D, который поставляет обоим. Этот диск характеризуется его прерываниями вещественной оси gmin, gmax и соответствующий находящийся на диске запас по амплитуде DGM = [gmin,gmax] и запас по фазе DPM соответствуйте или превысьте GM и PM.
Для получения дополнительной информации о дисковой модели усиления и изменения фазы, см. Алгоритмы.
DGM = getDGM(GM,PM,'tight')GM и PM.
Если GM и PM скаляры, затем дисковое усиление получений, которое может увеличиться или уменьшиться на коэффициент GM, и фаза, которая может увеличиться или уменьшиться PM.
Если GM и PM векторы из формы [glo,ghi] и [pmin,pmax] затем диск получает относительное усиление и изменения фазы этих областей значений.
Если любой GM или PM [], это удаляет соответствующее ограничение на размер диска.
Выход имеет форму DGM = [gmin,gmax], и описывает диск, который представляет абсолютные изменения усиления в той области значений. Например, DGM = [0.8,1.8] усиление моделей, которое может варьироваться от 0.8 раза номинальной стоимости к 1.8 раза номинальной стоимости и изменениям фазы, определенным дисковой геометрией. Этот диск может иметь ненулевой скос (см. Алгоритмы). Используйте DGM создать umargin блокируйтесь это моделирует, они получают и изменения фазы.
Найдите самый маленький находящийся на диске запас по амплитуде, который представляет родственника изменение усиления ±6 дБ относительно номинальной стоимости и изменение фазы ±40 °. Преобразуйте изменение усиления в абсолютные единицы.
GM = db2mag(6)
GM = 1.9953
PM = 40;
DGM = getDGM(GM,PM,'tight')DGM = 1×2
0.4299 1.9953
DGM описывает диск что модели и усиление и изменения фазы. Значения в DGM представляйте область значений изменения усиления в отсутствие изменения фазы. Обратите внимание на то, что DGM область значений немного больше, чем заданный [1/GM,GM] расположитесь, когда требование запаса по фазе является более строгим и определяет размер диска. Визуализируйте полный спектр усиления и изменений фазы, представленных DGM.
diskmarginplot(DGM)
'tight'ограничение вычисляет самый маленький диск, который поставляет и целевое усиление и изменения фазы, который не обязательно представляет симметричную область значений усиления. В этом случае диск представляет усиление, которое может уменьшить несколько больше, чем это может увеличиться. Исследуйте диск неопределенности, заданной этим конкретным DGM.
diskmarginplot(DGM,'disk')
Чтобы осуществить симметричное изменение усиления, используйте 'balanced' опция.
Определите находящийся на диске запас по амплитуде, который поставляет симметричное изменение усиления 5 дБ и изменение фазы 30 градусов.
GM = db2mag(5);
PM = 30;
DGM = getDGM(GM,PM,'balanced')DGM = 1×2
0.5623 1.7783
'balanced'ограничение моделирует диск неопределенности, которая симметрична вокруг номинальной стоимости. Функция возвращает симметричный находящийся на диске запас по амплитуде DGM = [gmin,gmax], с gmin=1/gmax.
diskmarginplot(DGM)
В этом случае, DPM немного превышает целевое изменение фазы и DGM равно целевому изменению усиления.
Определите находящийся на диске запас по амплитуде, соответствующий, чтобы получить изменения между 90% и 160% номинальной стоимости, и изменения фазы от-15 до +15 градусов.
gainRange = [0.9,1.6];
phaseRange = [-15,15];
DGMt = getDGM(gainRange,phaseRange,'tight')DGMt = 1×2
0.8603 1.6000
'tight'ограничение моделирует самый маленький диск, который поставляет целевое усиление и изменения фазы. Этот диск моделируется с изменением усиления, которое скашивается к увеличению усиления.
В качестве альтернативы можно использовать 'balanced'опция, чтобы ограничить находящийся на диске запас по амплитуде к симметричной области значений формы gmin = 1/gmax. Это означает, что усиление может увеличиться или уменьшиться равной суммой.
DGMb = getDGM(gainRange,phaseRange,'balanced')DGMb = 1×2
0.6250 1.6000
Визуализируйте область значений одновременного усиления и изменений фазы, соответствующих обеим областям значений усиления.
diskmarginplot([DGMt;DGMb])
Сбалансированная область значений DGMb моделирует большую, симметричную область значений усиления (gmin = 1/gmax) и большие изменения фазы, чем те вы задаете. Если вы уверены, что усиление варьируется больше по одному направлению, чем другой в вашей системе, то эта сбалансированная сила модели чрезмерно консервативна.
Определите сбалансированные находящиеся на диске области значений запаса по амплитуде, который поставляет изменения усиления ±4 дБ, ±6 дБ и ±12 дБ и изменение фазы ±30 °. Можно получить все находящиеся на диске области значений усиления целиком путем укладки желаемых целевых диапазонов в вектор-столбец.
GM = db2mag([4;6;12]);
PM = 30;
DGM = getDGM(GM,PM,'balanced')DGM = 3×2
0.5774 1.7321
0.5012 1.9953
0.2512 3.9811
diskmarginplot(DGM)
Каждая строка в матричном DGM дает находящееся на диске изменение усиления для соответствующей записи в GM. Например, самый маленький сбалансированный (симметричный) диск, который получает изменение усиления ±4 дБ и изменение фазы ±30 °, задан DGM(1,:) = [0.58 1.73].
Этот диск представляет несколько больше, чем цель ±4 дБ, для того, чтобы получить полное целевое изменение усиления ±30 °. Для целей ±6 дБ и ±12 дБ, диск соответствует целевому изменению усиления точно, но соответствующие диски описывают большие изменения фазы.
DGM — Смоделированная область значений относительного изменения усиленияСмоделированная область значений относительного изменения усиления, возвращенного как двухэлементный вектор из формы [gmin,gmax], где gmin <1 и gmax > 1. Например, DGM = [0.8 1.5] представляет усиление, которое может варьироваться между 80% и 150% его номинальной стоимости (то есть, изменение фактором между 0,8 и 1.5). gmin может быть отрицательным, задав область значений относительного изменения усиления, которое включает изменение в знак. Когда вы используете 'balanced' опция, изменение усиления симметрично, то есть, усиление может увеличиться или уменьшиться той же суммой (gmin = 1/gmax).
Область значений [gmin,gmax] описывает диск усиления и неопределенности фазы, где усиление может варьироваться [gmin,gmax] и фаза может варьироваться суммой, определенной дисковой геометрией. Например, следующий график показывает диск, охарактеризованный DGM = [0.5,2] (Для получения дополнительной информации о находящейся на диске модели неопределенности, см. Алгоритмы). Соответствующее изменение фазы (возвратился в DPM) ±30 °.
![Uncertainty disk characterized by DGM = [0.5,2]](disk_dgm_argdesc.png)
В общем случае DGM или соответствующий DPM может получить большие области значений изменения, чем те, вы задаете с входными параметрами GM и PM. Диск всегда получает, по крайней мере, заданные изменения.
Если GM вектор-столбец или матрица, представляющая несколько целевых диапазонов изменения усиления, DGM матрица 2D столбца формы [gmin1,gmax1; ...;gminN,gmaxN], где каждая строка является соответствующей находящейся на диске областью значений усиления.
DPM — Находящееся на диске изменение фазыНаходящийся на диске запас по фазе, возвращенный как двухэлементный вектор из формы [-pm,pm]. Объем изменения фазы определяется геометрией диска, описанного DGM (см. Алгоритмы).
Если PM вектор-столбец или матрица, представляющая несколько целевых диапазонов изменения фазы, DPM матрица 2D столбца формы [-pm1,pm1; ...;-pmN,pmN], где каждая строка является соответствующей находящейся на диске областью значений усиления.
umargin и diskmargin усиление модели и изменения фазы отдельной обратной связи образовывают канал как зависимый частотой мультипликативный фактор F (s) умножение номинального ответа разомкнутого контура L (s), такой, что встревоженным ответом является L (s) F (s). Факторный F (s) параметрируется:
В этой модели,
δ (s) является ограниченной усилением динамической неопределенностью, нормированной так, чтобы это всегда варьировалось в единичном диске (|| δ || ∞ <1).
ɑ устанавливает сумму усиления и изменения фазы, смоделированного F. Для фиксированного σ параметр ɑ управляет размером диска. Для ɑ = 0, мультипликативный фактор равняется 1, соответствуя номинальному L.
σ, названный skew, смещает смоделированную неопределенность к увеличению усиления или уменьшению усиления.
Факторный F принимает значения в диске, сосредоточенном на вещественной оси и содержащий номинальную стоимость F = 1. Диск характеризуется его прерыванием DGM = [gmin,gmax] с вещественной осью. gmin <1 и gmin > 1 минимальные и максимальные относительные изменения в усилении, смоделированном F, в номинальной фазе. Неопределенность фазы, смоделированная F, является областью значений DPM = [-pm,pm] из значений фазы в номинальном усилении (|F | = 1). Например, в следующем графике, правая сторона показывает диску F, который пересекает вещественную ось в интервале [0.71 1.4]. Левая сторона показывает, что этот диск моделирует изменение усиления ±3 дБ и изменение фазы ±19 °.
DGM = [0.71,1.4]
F = umargin('F',DGM)
plot(F)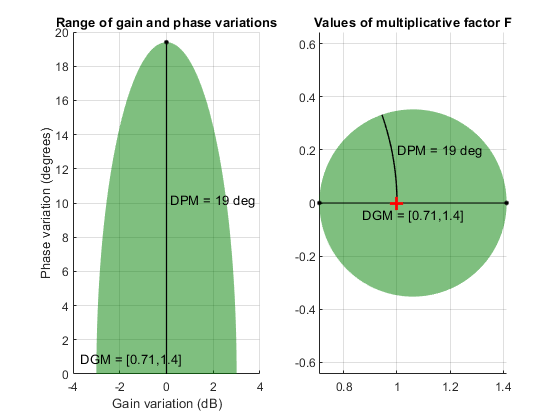
getDGM преобразует целевое усиление и изменения фазы, что вы хотите смоделировать в находящуюся на диске область значений изменения усиления DGM. Эта область значений полностью характеризует диск F. Соответствующая фаза располагается DPM таким образом определяется DGM и дисковая модель.
Для получения дальнейшей информации о модели неопределенности для усиления и изменений фазы, смотрите, что Анализ Устойчивости Использует Дисковые Поля.