hankelmr

Минимальное приближение степени (MDA) Ганкеля без балансировки

Синтаксис

GRED = hankelmr(G)
GRED = hankelmr(G,order)
[GRED,redinfo] = hankelmr(G,key1,value1,...)
[GRED,redinfo] = hankelmr(G,order,key1,value1,...)

Описание

hankelmr возвращает уменьшаемую модель GRED порядка из G и массив структур redinfo содержа ошибку, связанную упрощенной модели и сингулярных значений Ганкеля исходной системы.

Связанная ошибка вычисляется на основе сингулярных значений Ганкеля G. Для устойчивой системы сингулярные значения Ганкеля указывают на соответствующую энергию состояния системы. Следовательно, уменьшаемый порядок может быть непосредственно определен путем исследования системы Ганкель СВ, σ ι.

Только с одним входным параметром G, функция покажет график сингулярного значения Ганкеля исходной модели и запросит номер заказа модели, чтобы уменьшать.

Этот метод гарантирует, что ошибка привязала норму по бесконечности аддитивной ошибки ∥G-GRED∥ ∞ для хорошо подготовленной модели уменьшал проблемы [1]:

${‖ G - G r e d ‖}_{\infty} \leq 2 \sum_{k + 1}^{n} σ_{i}$

Примечание

Кажется, что этот метод похож на аддитивные стандартные программы снижения сложности модели balancmr и schurmr, но на самом деле это может произвести более надежную уменьшаемую модель порядка, когда желаемая упрощенная модель имеет почти управляемые и/или заметные состояния (имеет сингулярные значения Ганкеля близко к точности машины). hankelmr затем выберет оптимальную уменьшаемую систему, чтобы удовлетворить, ошибка связала критерий независимо порядок, каждый является наивно избранным вначале.

Эта таблица описывает входные параметры для hankelmr.

Аргумент	Описание
`G`	Модель LTI, которая будет уменьшаться (без любых других входных параметров построит ее сингулярные значения Ганкеля и запросит уменьшаемый порядок),
`ORDER`	(Необязательно) целое число для желаемого порядка упрощенной модели, или опционально вектор упаковывается желаемыми порядками для пакетных запусков

Пакетный запуск сериала различных уменьшаемых моделей порядка может быть сгенерирован путем определения order = x:y, or a vector of integers. По умолчанию вся антиустойчивая часть системы сохранена, потому что с точки зрения устойчивости управления, избавление от нестабильного состояния (состояний) опасно, чтобы смоделировать систему.

'MaxError' может быть задан тем же способом как альтернатива для 'ORDER'. В этом случае уменьшаемый порядок будет определен когда сумма хвостов пределов sv Ганкеля 'MaxError'.

Аргумент	Значение	Описание
`'MaxError'`	Вещественное число или вектор из различных ошибок	Уменьшайте, чтобы достигнуть H _∞ ошибка. Когда существующий, `'``MaxError``'` переопределения `ORDER` входной параметр.
`'Weights'`	`{Wout,Win}` cellArray	Оптимальный 1x2 массив ячеек весов LTI `Wout` (выведите) и `Win` входной параметр. Значением по умолчанию для обоих является идентичность. Веса должны быть обратимыми.
`'Display'`	`'on'` или `'off'`	Отобразите сингулярные графики Ганкеля (`'off'` по умолчанию).
`'Order'`	Целое число, векторный или массив ячеек	Порядок упрощенной модели. Используйте только если не заданный в качестве 2-го аргумента.

Веса на исходном входе модели и/или выходе могут заставить алгоритм снижения сложности модели фокусироваться на некотором частотном диапазоне интересов. Но веса должны быть устойчивой, минимальной фазой и обратимый.

Эта таблица описывает выходные аргументы.

Аргумент	Описание
`GRED`	LTI уменьшал модель порядка. Станьте многомерным массивом, когда введенный будет сериал различного массива порядка модели.
`REDINFO`	Массив структур с 4 полями: `REDINFO.ErrorBound` (привязанный ∥ G-GRED ∥∞) `REDINFO.StabSV` (Ганкель СВ устойчивой части G) `REDINFO.UnstabSV` (Ганкель СВ нестабильной части G) `REDINFO.Ganticausal` (Антипричинная часть MDA Ганкеля)

G может быть устойчивым или нестабильным, непрерывным или дискретным.

Примечание

Если size(GRED) не равно порядку, который вы задали. Оптимальный алгоритм MDA Ганкеля выбрал лучшую Минимальную Степень, Аппроксимированную, это может найти в допустимой точности машины.

Примеры

Учитывая непрерывную или дискретную, устойчивую или нестабильную систему, G, следующие команды могут получить набор уменьшаемых моделей порядка на основе ваших выборов:

rng(1234,'twister'); 
G = rss(30,5,4);
[g1, redinfo1] = hankelmr(G); % display Hankel SV plot
							 % and prompt for order (try 15:20)
[g2, redinfo2] = hankelmr(G,20); 
[g3, redinfo3] = hankelmr(G,[10:2:18]);
[g4, redinfo4] = hankelmr(G,'MaxError',[0.01, 0.05]);
for i = 1:4
	figure(i); eval(['sigma(G,g' num2str(i) ');']);
end

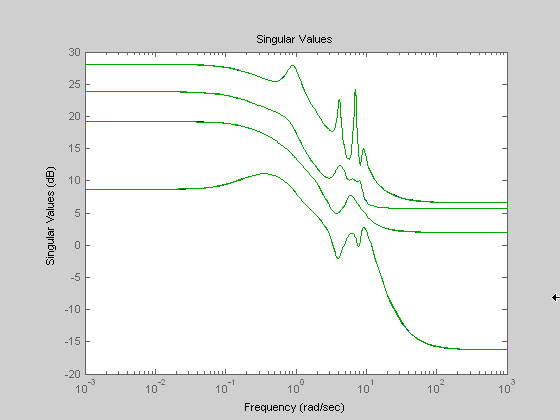
Диаграмма Боде Сингулярного значения G (с 30 состояниями, 5 выходных параметров, 4 входных параметров) показывает Диаграмму Боде сингулярного значения случайной системы G с 20 состояниями, 5 выходами и 4 входными параметрами. Ошибочная система между G и его Нулевой порядок, MDA Ганкеля имеет его норма по бесконечности, равняется всей функции передачи, как показано в Ошибочной Системе все-Передачи Между G и Нулевым Антипричинным Порядком G.

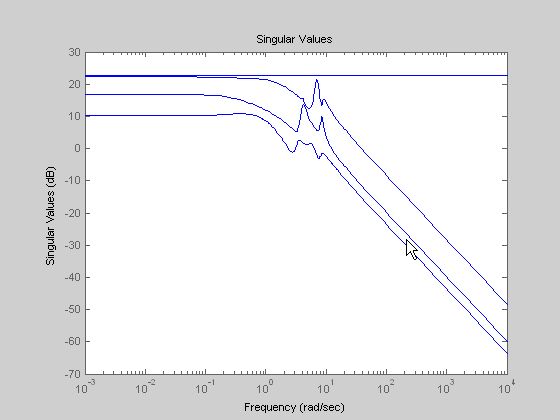
Нулевой порядок MDA Ганкеля и его ошибочный системный график сигмы получен через команды

[g0,redinfo0] = hankelmr(G,0);
sigma(G-redinfo0.Ganticausal)

Это интересное свойство все-передачи уникально в снижении сложности модели MDA Ганкеля.

Диаграмма Боде Сингулярного значения G (с 30 состояниями, 5 выходных параметров, 4 входных параметров)

Все-передайте ошибочную систему между G и нулевым антипричинным порядком G

Алгоритмы

Учитывая пространство состояний (A,B,C,D) системы и k, желаемого уменьшаемого порядка, следующие шаги произведут преобразование подобия, чтобы обрезать исходную систему в пространстве состояний до упрощенной модели порядка ^kth.

Найдите управляемость и наблюдаемость grammians P и Q.
Сформируйте дескриптор
$E = Q P - ρ^{2} I$
где $σ_{k} > ρ \geq σ_{k + 1}$ , и пространство состояний дескриптора
Возьмите SVD дескриптора E и разделите результат в форму усечения порядка ^kth
$\begin{array}{l} [\begin{matrix} E s - \bar{A} & \bar{B} \\ \bar{C} & \bar{D} \end{matrix}] = [\begin{matrix} ρ^{2} A^{T} + Q A P & Q B \\ C P & D \end{matrix}] \\ E = [U_{E 1}, U_{E 2}] [\begin{matrix} Σ_{E} 0 & 0 \\ 0 & 0 \end{matrix}] [\begin{matrix} V_{E 1}^{T} \\ V_{E 2}^{T} \end{matrix}] \end{array}$
Примените преобразование к системе в пространстве состояний дескриптора выше, мы имеем
$\begin{array}{l} [\begin{matrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{matrix}] = [\begin{matrix} U_{E 1}^{T} \\ U_{E 2}^{T} \end{matrix}] (ρ^{2} A^{T} + Q A P) [\begin{matrix} V_{E 1} & V_{E 2} \end{matrix}] \\ [\begin{matrix} B_{1} \\ B_{2} \end{matrix}] = [\begin{matrix} U_{E 1}^{T} \\ U_{E 2}^{T} \end{matrix}] [\begin{matrix} Q B & - C^{T} \end{matrix}] \\ [\begin{matrix} C_{1} & C_{2} \end{matrix}] = [\begin{matrix} C P \\ - ρ B^{T} \end{matrix}] [\begin{matrix} V_{E 1} & V_{E 2} \end{matrix}] \\ D_{1} = D \end{array}$
Сформируйте эквивалентную модель в пространстве состояний.
$[\begin{matrix} \tilde{A} & \tilde{B} \\ \tilde{C} & \tilde{D} \end{matrix}] = [\begin{matrix} \sum_{E}^{- 1} (A_{11} - A_{12} A_{22}^{†} A_{21}) & \sum_{E}^{- 1} (B_{1} - A_{12} A_{22}^{†} B_{2}) \\ C_{1} - C_{2} A_{22}^{†} A_{21} & D_{1} - C_{2} A_{22}^{†} B_{2} \end{matrix}]$
Итоговый ^kth приказывает, чтобы MDA Ганкеля был устойчивой частью вышеупомянутой реализации пространства состояний. Его антипричинная часть хранится в redinfo.Ganticausal.

Доказательство алгоритма MDA Ганкеля может быть найдено в [2]. Ошибочная система между исходной системой G и Нулевым Порядком MDA Ганкеля G0 является функцией все-передачи [1].

Ссылки

[1] Перчаточник, К., “Все Оптимальное Приближение Нормы Ганкеля Линейных Многомерных Систем и Их _{-ошибочные} Границы L”, Int J. Управление, издание 39, № 6, стр 1145-1193, 1984.

[2] Сафонов, M.G., Р.И. Чанг и D.J.N. Limebeer, “Оптимальное Снижение сложности модели Ганкеля для Неминимальных Систем”, Сделка IEEE на Автомате. Противоречие, издание 35, № 4, апрель 1990, стр 496-502.

Представлено до R2006a

Документация

hankelmr

Синтаксис

Описание

Примеры

Алгоритмы

Ссылки

Смотрите также

Документация Robust Control Toolbox

Поддержка