Кодер RS с целочисленным входом

Создание кода Рида-Соломона из целочисленных векторных данных

Библиотека:
Панель инструментов связи/Обнаружение и исправление ошибок/Блок

Описание

Блок целочисленного входного RS-кодера создает код Рида-Соломона.

Символами для кода являются целые числа между 0 и ^2M-1, которые представляют элементы конечного поля GF (^2M). Значением по умолчанию M является наименьшее целое число, которое больше или равно log2 (N + 1), то естьceil(log2(N+1)). Можно изменить значение M по умолчанию, указав примитивный многочлен для GF (^2M), как описано ниже в разделе Задание примитивного многочлена. Ограничения на M и N описаны в разделе Ограничения на M и длину N кодового слова.

Входные и выходные сигналы представляют собой целочисленные сигналы, представляющие сообщения и кодовые слова соответственно. Дополнительные сведения см. в разделе Длина входного и выходного сигнала в блоках RS.

Код Рида-Соломона (N, K) может исправлять до floor((N-K)/2) символьные ошибки (не битовые ошибки) в каждом кодовом слове.

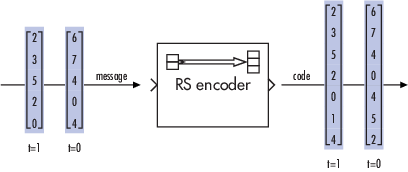
Предположим, что M = 3, N = ^23-1 = 7 и K = 5. Тогда сообщение является вектором длиной 5, записи которого являются целыми числами между 0 и 7. Соответствующее кодовое слово представляет собой вектор длиной 7, записи которого являются целыми числами между 0 и 7. Следующий рисунок иллюстрирует возможные входные и выходные сигналы для этого блока, когда длина N кодового слова установлена в 7, длина сообщения К установлена в 5и используются примитивные и генераторные полиномы по умолчанию.

Порты

Вход

развернуть все

`In` - Сообщение
целочисленный вектор-столбец

Сообщение, указанное как одно из следующих:

При отсутствии укорочения сообщения вектор целочисленного столбца (NC × K) -на-1 .
При укорочении сообщения вектор целочисленного столбца (NC × S) -на-1 .

NC - количество слов сообщения, K - длина сообщения K, S - длина укороченного сообщения S.

Примечание

Количество декодированных слов сообщения равно количеству кодовых слов.

Дополнительные сведения см. в разделе Длина входного и выходного сигнала в блоках RS.

Продукция

развернуть все

`Out` - Кодовое слово Рида - Соломона
целочисленный вектор-столбец

Кодовое слово Рида - Соломона, возвращаемое в виде вектора (NC × (N - K + S - P) -by-1 целочисленного столбца_. NC - количество кодовых слов, N - длина кодового слова N, K - длина сообщения K, S - длина укороченного сообщения S, P - количество проколов на кодовое слово.

Дополнительные сведения см. в разделе Длина входного и выходного сигнала в блоках RS.

Дополнительные сведения см. в разделе Поддерживаемые типы данных.

Параметры

развернуть все

`Codeword length N` - Длина кодового слова
`7` (по умолчанию) | целое число

Длина кодового слова, заданная как целое число.

Дополнительные сведения см. в разделах Ограничения для M и Длина N кодового слова и Длина входного и выходного сигнала в блоках RS.

`Message length K` - Длина слова сообщения
`3` (по умолчанию) | целое число

Длина слова сообщения, заданная как целое число в диапазоне [1, N-2], где N - длина кодового слова.

`Shortened message length S` - Сокращенная длина слова сообщения
`3` (по умолчанию) | целое число

Сокращенная длина слова сообщения, заданная как целое число, так что S ≤ K. Когда сокращенная длина сообщения S < длина сообщения K, код Рида-Соломона сокращается.

Значения N и K по-прежнему задаются для полноразмерного (N, K) кода, но декодирование сокращается до кода (N-K + S, S).

Зависимости

Чтобы включить этот параметр, выберите Указать укороченную длину сообщения.

`Generator polynomial` - Полином генератора
`rsgenpoly(7, 3, [], [], 'double')` (дефолт) | многочленный вектор характера | вектор строки двоичных знаков | набор из двух предметов вектор ряда Галуа

Генераторный полином со значениями в диапазоне [от 0 до ^2M-1], в порядке убывания мощности, заданными как одно из следующих:

Вектор многочлена. Дополнительные сведения см. в разделе Символьное представление многочленов.
Целочисленный вектор строки, представляющий коэффициенты генераторного многочлена в порядке степени убывания.
Целочисленный вектор строки Галуа, представляющий коэффициенты генераторного многочлена в порядке степени убывания.

Каждый коэффициент является элементом поля Галуа, определяемым примитивным многочленом. Дополнительные сведения см. в разделе Задание полинома генератора.

Пример: [1 3 1 2 3], что эквивалентно rsgenpoly(7,3)

Зависимости

Чтобы включить этот параметр, выберите Задать полином генератора (Specify generator polynomial).

`Primitive polynomial` - примитивный многочлен
`'X^3 + X + 1'` (по умолчанию) | вектор многочлена | двоичный вектор строки

Примитивный многочлен в порядке степени убывания. Этот многочлен имеет порядок M и определяет конечное поле Галуа GF (^2M), соответствующее целым числам, которые образуют слова сообщения и кодовые слова. Укажите примитивный многочлен как один из следующих:

Вектор многочлена. Дополнительные сведения см. в разделе Символьное представление многочленов.
Двоичный вектор строки, представляющий коэффициенты полинома генератора.

Дополнительные сведения см. в разделе Указание полинома примитива.

Пример: 'X^3 + X + 1', который является примитивным многочленом, используемым для (7,3) кода, de2bi(primpoly(3,'nodisplay'),'left-msb')

Зависимости

Чтобы включить этот параметр, выберите Задать примитивный полином.

`Puncture vector` - Вектор прокола
`[ones(2,1); zeros(2,1)]` (по умолчанию) | двоичный вектор столбца

Вектор прокола, заданный как вектор двоичного столбца (N-K) -by-1. Индексы элементов с1s представляют индексы символов данных, которые проходят через блок без изменений. Индексы элементов с 0s представляют индексы символов данных, которые проколоты или удалены из потока данных. Дополнительные сведения см. в разделе Прокалывание и стирание.

Примечание

Если кодер обрабатывает множество кодовых слов в кадре, то один и тот же шаблон прокола сохраняется для всех кодовых слов.

Зависимости

Чтобы включить этот параметр, выберите Код прокола.

Примеры модели

Reed-Solomon Coding with Erasures, Punctures, and Shortening in Simulink

Кодирование Рида-Соломона со стиранием, проколами и укорочением в Simulink

Настройка кодов Рида-Соломона (RS) для выполнения блочного кодирования со стиранием, проколами и укорочением.

Характеристики блока

Типы данных	`double` \| `integer` \| `single`
Многомерные сигналы	`no`
Сигналы переменного размера	`no`

Подробнее

развернуть все

Длина входного и выходного сигнала в блоках RS

Код Рида-Соломона имеет длину слова сообщения, K, или длину укороченного слова сообщения, S. Длина кодового слова равна N - K + S - P, где N - полная длина кодового слова, а P - количество проколов на кодовое слово. Когда нет укорочения сообщения, выражение длины кодового слова уменьшается до N - P, поскольку K = S. Если декодер обрабатывает несколько кодовых слов в кадре, то один и тот же шаблон прокола сохраняется для всех кодовых слов.

В этой таблице представлены выражения длины входного и выходного сигналов для кодера Рида-Соломона и декодера.

Обозначение y = NC × x обозначает, что y является целым числом, кратным x.

	Длина входного, выходного и выходного векторов
Кодер RS с целочисленным входом	Длина ввода (символы): NC × K Длина вывода (символы): NC × (N-P)	Длина ввода (символы): NC × S Длина вывода (символы): NC × (N-K + S-P)
Декодер RS с целочисленным выходом	Длина ввода (символы): NC × (N-P) Длина стирания (символы): NC × (N-P) Длина вывода (символы): NC × K	Длина ввода (символы): NC × (N-K + S-P) Длина стирания (символы): NC × (N-K + S-P) Длина вывода (символы): NC × S

Длина входного, выходного и выходного векторов

Кодер блоков RS

Сокращение сообщений не используется

Используется сокращение сообщений

Кодер RS с целочисленным входом

Длина ввода (символы):

NC × K

Длина вывода (символы):

NC × (N-P)

Длина ввода (символы):

NC × S

Длина вывода (символы):

NC × (N-K + S-P)

Декодер RS с целочисленным выходом

Длина ввода (символы):

NC × (N-P)

Длина стирания (символы):

NC × (N-P)

Длина вывода (символы):

NC × K

Длина ввода (символы):

NC × (N-K + S-P)

Длина стирания (символы):

NC × (N-K + S-P)

Длина вывода (символы):

NC × S

N - длина кодового слова.
K - длина слова сообщения.
S - укороченная длина слова сообщения.
NC - количество кодовых слов (и слов сообщения).
P - число проколов и равно числу нулей в векторе проколов.
M - степень примитивного многочлена. Каждая группа из М битов представляет целое число между 0 и 2^M–1 которая принадлежит конечному полю Галуа GF(2^M).

Дополнительные сведения о представлении данных для кодов Рида-Соломона см. в разделе Целочисленный формат (только для Рида-Соломона).

Ограничения на M и длину кодового слова N

Если не выбран параметр Указать примитивный многочлен, допустимые значения длины кодового слова N составляют от 7 до 65535. В этом случае блок использует примитивный многочлен степени по умолчанию M = ceil(log2(N+1)). Можно отобразить полином примитива по умолчанию, выполнив команду primpoly(ceil(log2(N+1))).
Если выбран параметр Задать примитивный многочлен (Specify primitive polynomial), допустимые значения степени примитивного многочлена M составляют от 3 до 16. Допустимые значения для N в этом случае составляют от 7 до ^2M-1. Выбор параметра «Указать примитивный многочлен» позволяет задать примитивный многочлен, определяющий конечное поле GF (^2M), которое соответствует значениям, образующим слова сообщения и кодовые слова.

Задание полинома примитива

Можно задать примитивный многочлен, определяющий конечное поле GF (^2M), соответствующее целым числам, которые образуют сообщения и кодовые слова. Для этого сначала выберите Задать примитивный полином (Specify primitive polynomial). Затем в текстовом поле Примитивный многочлен введите двоичный вектор строки, который представляет примитивный многочлен над GF ⁽2M), в порядке убывания степеней. Например, чтобы задать полином x3 + x + 1, введите вектор[1 0 1 1].

Если не выбран параметр Задать примитивный многочлен (Specify primitive polynomial), блок использует примитивный многочлен по умолчанию степени M = ceil (log2 (N + 1)). Можно отобразить полином по умолчанию, введяprimpoly(ceil(log2(N+1))) в подсказке MATLAB ®.

Задание полинома генератора

Выберите Задать полином генератора (Specify generator polynomial), чтобы включить параметр Полином генератора (Generator polynomial) для задания полинома генератора кода Рида-Соломона. Введите целочисленный вектор строки со значениями элементов от 0 до ^2M-1. Вектор представляет многочлен в порядке убывания степеней, коэффициенты которого являются элементами GF (^2M), представленными в целочисленном формате. Дополнительные сведения о целочисленном и двоичном форматах см. в разделе Целочисленный формат (только для Рида-Соломона). Генераторный многочлен должен быть равен многочлену с такой факторизованной формой:

g (x) = (x ⁺ αb) ^(x + αb ^{+ 1}) (x + ^{αb + 2).}.. (x + αb + N-K-1)

α - примитивный элемент поля Галуа, над которым определено входное сообщение, а b - целое число.

Если не выбран параметр Задать полином генератора (Specify generator polynomial), блок использует для кодирования Рида-Соломона полином генератора по умолчанию, соответствующий b = 1. Можно отобразить полином генератора по умолчанию, выполнив командуrsgenpoly.

Если используется примитивный многочлен по умолчанию (не выбран параметр «Указать примитивный многочлен»), используется полином генератора по умолчанию rsgenpoly(N,K), где N = 2^M-1.
Если не используется примитивный многочлен по умолчанию (выбран параметр Указать примитивный многочлен) и указывается примитивный многочлен как poly, генераторный многочлен rsgenpoly(N,K,poly).

Примечание

Степень полинома генератора равна N − K, где N - длина кодового слова, а K - длина слова сообщения.

Прокалывание и стирание

1s и 0s имеют совершенно противоположные значения для векторов прокола и стирания.

В векторе прокола,

1 означает, что символ данных проходит через блок без изменений.
0 означает, что символ данных должен быть проколот или удален из потока данных.

В векторе стирания

1 означает, что символ данных должен быть заменен символом стирания.
0 означает, что символ данных проходит через блок без изменений.

Эти условные обозначения применимы как к кодеру, так и к декодеру. Дополнительные сведения см. в разделах Укорочение, прокалывание и стирание.

Поддерживаемые типы данных

Порт	Поддерживаемые типы данных
В	Плавающая точка с двойной точностью Плавающая точка с одинарной точностью 8-, 16- и 32-разрядные целые числа со знаком 8-, 16- и 32-разрядные целые числа без знака
Из	Плавающая точка с двойной точностью Плавающая точка с одинарной точностью 8-, 16- и 32-разрядные целые числа со знаком 8-, 16- и 32-разрядные целые числа без знака

Парный блок

Декодер RS с целочисленным выходом

Алгоритмы

Этот объект реализует алгоритм, входы и выходы, описанные в разделе Алгоритмы декодирования только ошибок BCH и RS.

Расширенные возможности

Создание кода C/C + +
Создайте код C и C++ с помощью Simulink ® Coder™

См. также

Представлен до R2006a

Документация

Кодер RS с целочисленным входом

Описание

Порты

Вход

`In` - Сообщение
целочисленный вектор-столбец

Продукция

`Out` - Кодовое слово Рида - Соломона
целочисленный вектор-столбец

Параметры

`Codeword length N` - Длина кодового слова
`7` (по умолчанию) | целое число

`Message length K` - Длина слова сообщения
`3` (по умолчанию) | целое число

`Shortened message length S` - Сокращенная длина слова сообщения
`3` (по умолчанию) | целое число

Зависимости

Зависимости

`Primitive polynomial` - примитивный многочлен
`'X^3 + X + 1'` (по умолчанию) | вектор многочлена | двоичный вектор строки

Зависимости

`Puncture vector` - Вектор прокола
`[ones(2,1); zeros(2,1)]` (по умолчанию) | двоичный вектор столбца

Зависимости

Примеры модели

Кодирование Рида-Соломона со стиранием, проколами и укорочением в Simulink

Характеристики блока

Подробнее

Длина входного и выходного сигнала в блоках RS

Ограничения на M и длину кодового слова N

Задание полинома примитива

Задание полинома генератора

Прокалывание и стирание

Поддерживаемые типы данных

Парный блок

Алгоритмы

Расширенные возможности

Создание кода C/C + +
Создайте код C и C++ с помощью Simulink ® Coder™

См. также

Блоки

Объекты

Функции

Документация по инструментам связи

Поддержка

Документация

Кодер RS с целочисленным входом

Описание

Порты

Вход

In - Сообщение целочисленный вектор-столбец

Продукция

Out - Кодовое слово Рида - Соломона целочисленный вектор-столбец

Параметры

Codeword length N - Длина кодового слова 7 (по умолчанию) | целое число

Message length K - Длина слова сообщения 3 (по умолчанию) | целое число

Shortened message length S - Сокращенная длина слова сообщения 3 (по умолчанию) | целое число

Зависимости

Зависимости

Primitive polynomial - примитивный многочлен 'X^3 + X + 1' (по умолчанию) | вектор многочлена | двоичный вектор строки

Зависимости

Puncture vector - Вектор прокола [ones(2,1); zeros(2,1)] (по умолчанию) | двоичный вектор столбца

Зависимости

Примеры модели

Кодирование Рида-Соломона со стиранием, проколами и укорочением в Simulink

Характеристики блока

Подробнее

Длина входного и выходного сигнала в блоках RS

Ограничения на M и длину кодового слова N

Задание полинома примитива

Задание полинома генератора

Прокалывание и стирание

Поддерживаемые типы данных

Парный блок

Алгоритмы

Расширенные возможности

Создание кода C/C + + Создайте код C и C++ с помощью Simulink ® Coder™

См. также

Блоки

Объекты

Функции

Документация по инструментам связи

Поддержка

`In` - Сообщение
целочисленный вектор-столбец

`Out` - Кодовое слово Рида - Соломона
целочисленный вектор-столбец

`Codeword length N` - Длина кодового слова
`7` (по умолчанию) | целое число

`Message length K` - Длина слова сообщения
`3` (по умолчанию) | целое число

`Shortened message length S` - Сокращенная длина слова сообщения
`3` (по умолчанию) | целое число

`Primitive polynomial` - примитивный многочлен
`'X^3 + X + 1'` (по умолчанию) | вектор многочлена | двоичный вектор строки

`Puncture vector` - Вектор прокола
`[ones(2,1); zeros(2,1)]` (по умолчанию) | двоичный вектор столбца

Создание кода C/C + +
Создайте код C и C++ с помощью Simulink ® Coder™