Exponenta Banner
exponenta event banner

allmargin

Запас усиления, запас фазы, запас задержки и переходные частоты

свернуть все на странице

Синтаксис

S = аллмаргин (L)
S = аллмаргин (mag, phase, w, ts)

Описание

пример

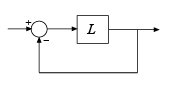
S = allmargin(L) вычисляет запас усиления, запас фазы, запас задержки и соответствующие частоты пересечения для контура отрицательной обратной связи SISO или MIMO с откликом разомкнутого контура L. Цикл отрицательной обратной связи вычисляется как feedback(L,eye(M)), где M - количество входов и выходов в L.

Для системы MIMO: allmargin возвращает пределы стабильности цикла в момент времени для системы замкнутого цикла с отрицательной обратной связью. Использовать allmargin найти классические поля любой модели SISO или MIMO, включая модели с задержками.

пример

S = allmargin(mag,phase,w,ts) вычисляет пределы стабильности на основе данных частотной характеристики mag, phase, wи время выборки, ts.

Примеры

свернуть все

Открыть сценарий в реальном времени

В этом примере рассмотрим функцию передачи с разомкнутым контуром SISO L данное,

L = 25s3 + 10s2 + 10s + 10

L = tf(25,[1 10 10 10]);

Найти пределы стабильности L.

S = allmargin(L)
S = struct with fields:
     GainMargin: 3.6000
    GMFrequency: 3.1623
    PhaseMargin: 29.1104
    PMFrequency: 1.7844
    DelayMargin: 0.2847
    DMFrequency: 1.7844
         Stable: 1

Продукция S - структура с классическими полями и их соответствующими переходными частотами контура отрицательной обратной связи L.

Открыть сценарий в реальном времени

В этом примере рассмотрим модель пространства состояний MIMO L с 2 входами и 2 выходами.

Загрузите данные.

load('mimoStateSpaceModel.mat','L')

Найдите классические поля для системы MIMO.

S = allmargin(L)
S=2×1 struct array with fields:
    GainMargin
    GMFrequency
    PhaseMargin
    PMFrequency
    DelayMargin
    DMFrequency
    Stable

Продукция S представляет собой структурный массив 2 на 1 классических полей и их соответствующих частот пересечения. Например, S(1) относится к пределам устойчивости первого канала обратной связи ввода-вывода со всеми остальными замкнутыми контурами.

Открыть сценарий в реальном времени

Для этого примера загрузите invertedPendulumArray.mat, который содержит массив 3 на 3 перевернутых моделей SISO маятника. Масса маятника изменяется при переходе от модели к модели вдоль одного столбца sysи длина маятника изменяется при движении вдоль одного ряда. Используемые значения массы составляют 100 г, 200 г и 300 г, а используемые длины маятников составляют соответственно 3 м, 2 м и 1 м.

Column1Column2Column3Row1100g, 3m100 г, 2m100 г, 1mRow2200 г, 3m200 г, 2m200 г, 1mRow3300 г, 3m300 г, 2m300 г, 1 м

load('invertedPendulumArray.mat','sys');
size(sys)
3x3 array of transfer functions.
Each model has 1 outputs and 1 inputs.

Найдите поля стабильности для всех моделей в массиве.

S = allmargin(sys)
S=3×3 struct array with fields:
    GainMargin
    GMFrequency
    PhaseMargin
    PMFrequency
    DelayMargin
    DMFrequency
    Stable

allmargin возвращает массив структуры 3 на 3 S, в котором каждая запись представляет собой структуру, содержащую поля устойчивости соответствующей записи в sys. Например, пределы устойчивости модели с массой маятника 100 г и длиной 2 м содержатся в S(1,2).

Открыть сценарий в реальном времени

Для этого примера загрузите данные частотной характеристики системы с разомкнутым контуром, состоящей из величин m и значения фаз p измеряется на частотах в w.

load('openLoopFRData.mat','m','p','w','ts');

Вычислять пределы стабильности с использованием данных частотной характеристики.

S = allmargin(m,p,w,ts)
S = struct with fields:
     GainMargin: 0.6249
    GMFrequency: 1.2732
    PhaseMargin: [-90.0000 48.9853]
    PMFrequency: [1.0000 1.5197]
    DelayMargin: [4.7124 0.5626]
    DMFrequency: [1.0000 1.5197]
         Stable: NaN

Продукция S - структура с классическими полями и их соответствующими переходными частотами. С тех пор allmargin не может оценить стабильность для моделей данных частотного отклика, S.Stable = NaN.

Входные аргументы

свернуть все

Отклик с разомкнутым контуром, заданный как динамическая модель системы. L может быть SISO или MIMO, если он имеет одинаковое количество входов и выходов. allmargin вычисляет классические пределы устойчивости для замкнутой системы с отрицательной обратной связью feedback(L,eye(M)):

Расчет пределов устойчивости системы положительной обратной связи feedback(L,eye(M),+1), использовать allmargin(-L).

При наличии контроллера P и растение C, можно вычислить пределы устойчивости для изменений коэффициента усиления и фазы на входах или выходах установки. Из следующей схемы:

  • Для расчета маржи на заводских выходах установите L = P*C.

  • Для расчета маржи на заводских вводах установите L = C*P.

L может быть непрерывным временем или дискретным временем. Если L является обобщенной государственно-пространственной моделью (genss или uss), то allmargin использует текущее или номинальное значение всех блоков проекта управления в L.

Если L является моделью данных частотного отклика (например, frd), то allmargin вычисляет поля на каждой частоте, представленной в модели. Функция возвращает поля на частоте с наименьшим запасом устойчивости.

Если L является массивом модели, то allmargin вычисляет поля для каждой модели в массиве.

Величина отклика системы в абсолютных единицах, заданная как массив 3-D. mag - массив M-на-M-на-N, где M - количество входов или выходов, а N - количество частотных точек. Для получения дополнительной информации о получении mag, см. раздел Получение данных о величине и фазе, а также о величине и фазе системы MIMO.

Фаза отклика системы в градусах, заданная как массив 3-D. phase - массив M-на-M-на-N, где M - количество входов или выходов, а N - количество частотных точек. Для получения дополнительной информации о получении phase, см. раздел Получение данных о величине и фазе, а также о величине и фазе системы MIMO.

Частоты, на которых получают величину и фазовые значения отклика системы, заданные в виде вектора-столбца. Можно указать частотный вектор w в любых единицах; allmargin возвращает частоты в тех же единицах. allmargin интерполяция между частотными точками для аппроксимации истинных полей стабильности.

Время выборки, указанное как целое число. allmargin использование ts для поиска полей стабильности из данных частотной характеристики.

  • Для моделей непрерывного времени установите ts = 0.

  • Для дискретно-временных моделей ts - положительное целое число, представляющее период выборки. Для обозначения дискретно-временной модели с неопределенным временем выборки установите ts = -1.

Выходные аргументы

свернуть все

Поля усиления, фазы и задержки, возвращаемые в виде структурного массива.

Продукция S - структура со следующими полями:

  • GMFrequency: Все частоты пересечения -180 ° (по модулю 360 °) вrad/TimeUnit, где TimeUnit - единицы времени, указанные в TimeUnit имущество L.

  • GainMarginСоответствующие коэффициенты усиления, определяемые как 1/G, где G - коэффициент усиления при частоте пересечения -180 °. Маржа прибыли находится в абсолютных единицах.

  • PMFrequency: Все 0-dB частоты кроссовера в rad/TimeUnit, где TimeUnit - единицы времени, указанные в TimeUnit имущество L.

  • PhaseMarginСоответствующие поля фаз в градусах.

  • DMFrequency и DelayMargin: DelayMargin - максимальная задержка, которую система может выдержать до потери стабильности. DMFrequency содержит критические частоты, соответствующие полям задержки. Пределы задержки задаются в единицах времени системы для систем непрерывного времени и кратных времени выборки для систем дискретного времени.

  • Stable: 1 если номинальная система с замкнутым контуром стабильна, 0 если нестабильно, и NaN если стабильность не может быть оценена. В общем, allmargin не может оценить стабильность frd система.

Когда L - система MIMO M-by-M, S является массивом структуры M-by-1. Например, S(j) дает пределы стабильности для j-го канала обратной связи со всеми остальными замкнутыми контурами (поля с одним контуром в момент времени).

Совет

  • allmargin предполагает, что система с откликом с разомкнутым контуром L является системой отрицательной обратной связи. Расчет классических пределов устойчивости системы положительной обратной связи feedback(L,eye(M),+1), использовать allmargin(-L).

  • Чтобы вычислить классические поля для системы, смоделированной в Simulink ®, сначала линеаризуйте модель, чтобы получить отклик с разомкнутым контуром в определенной рабочей точке. Затем используйтеallmargin для вычисления классических пределов устойчивости для линеаризованной системы. Дополнительные сведения см. в разделе Поля стабильности модели Simulink (надёжная панель инструментов управления).

См. также

| | (инструментарий надежного управления)

Темы

Представлен до R2006a

Документация по панели инструментов системы управления

Поддержка