diskmargin

Дисковые пределы стабильности петель обратной связи

Синтаксис

[DM, MM] = дискмаргин (L)

MMIO = дискмаргин (P, C)

___ = дискмаргин (___, сигма)

Описание

[DM,MM] = diskmargin(L) вычисляет пределы стабильности на основе диска для цикла отрицательной обратной связи SISO или MIMO feedback(L,eye(N)), где N - количество входов и выходов в L.

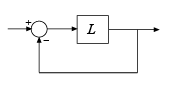
Diagram of a feedback loop consisting of L with unit negative feedback.

diskmargin команда возвращает поля стабильности loop-at-a-time в DM и поля нескольких шлейфов в MM. Дисковый анализ запаса обеспечивает более надежную гарантию стабильности, чем классический коэффициент усиления и запас по фазе. Общие сведения о полях диска см. в разделе Анализ стабильности с использованием полей диска.

пример

MMIO = diskmargin(P,C) вычисляет пределы устойчивости при рассмотрении независимых, параллельных вариаций как на входах установки, так и на выходах установки по контуру отрицательной обратной связи следующей диаграммы.

Diagram of a feedback loop consisting of P*C with unit negative feedback, with arrows indicating the inputs and outputs of the plant P.

пример

___ = diskmargin(___,sigma) задает дополнительный параметр перекоса, который смещает моделируемое усиление и изменение фазы в сторону увеличения усиления (положительное sigma) или снижение коэффициента усиления (отрицательное sigma). Этот аргумент можно использовать для проверки относительной чувствительности полей устойчивости к увеличению или уменьшению. Этот аргумент можно использовать с любым из предыдущих синтаксисов.

Примеры

свернуть все

Границы диска контура обратной связи MIMO

Открыть сценарий в реальном времени

diskmargin вычисляет как закольцовываемые, так и многолучевые поля диска. Этот пример иллюстрирует, что поля цикла в момент времени могут дать чрезмерно оптимистичную оценку истинной надежности циклов обратной связи MIMO. Поля отдельных петель могут быть чувствительны к небольшим возмущениям в других петлях, а поля петель в момент времени игнорируют такие взаимодействия петель.

Рассмотрим двухканальный цикл обратной связи MIMO на следующем рисунке.

Модель завода P берется из полей стабильности MIMO для вращающегося спутника и C - статический коэффициент усиления обратной связи на выходе [1 -2; 0 1].

a = [0 10;-10 0]; 
b = eye(2); 
c = [1 10;-10 1]; 
P = ss(a,b,c,0); 
C = [1 -2;0 1];

Вычислите дисковые маржи на выходе предприятия. Отклик разомкнутого контура с отрицательной обратной связью на выходе установки составляет Lo = P*C.

Lo = P*C;
[DMo,MMo] = diskmargin(Lo);

Изучите поля диска, возвращенные в массиве структуры DM. Каждая запись в DM содержит поля устойчивости соответствующего канала обратной связи.

DMo(1)

ans = struct with fields:
           GainMargin: [0 Inf]
          PhaseMargin: [-90 90]
           DiskMargin: 2
           LowerBound: 2
           UpperBound: 2
            Frequency: Inf
    WorstPerturbation: [2x2 ss]

DMo(2)

ans = struct with fields:
           GainMargin: [0 Inf]
          PhaseMargin: [-90 90]
           DiskMargin: 2
           LowerBound: 2
           UpperBound: 2
            Frequency: 0
    WorstPerturbation: [2x2 ss]

Поля петли во время являются превосходными (бесконечный запас усиления и запас фазы 90 °). Далее изучите поля многолучевого дискаMMo. Они учитывают независимые и одновременные изменения усиления (фазы) в обоих контурах обратной связи. Это более реалистичная оценка, поскольку неопределенность растений обычно влияет на оба канала одновременно.

MMo

MMo = struct with fields:
           GainMargin: [0.6839 1.4621]
          PhaseMargin: [-21.2607 21.2607]
           DiskMargin: 0.3754
           LowerBound: 0.3754
           UpperBound: 0.3762
            Frequency: 0
    WorstPerturbation: [2x2 ss]

Многолучевое усиление и фазовые поля намного слабее, чем их аналоги с контуром в момент времени. Стабильность гарантируется только в том случае, если коэффициент усиления в каждом контуре изменяется менее чем на 1,46, или когда фаза каждого контура изменяется менее чем на 21 °. Использоватьdiskmarginplot визуализировать поля усиления и фазы как функцию частоты.

diskmarginplot(Lo)

Figure contains 2 axes. Axes 1 contains an object of type line. This object represents Lo. Axes 2 contains an object of type line. This object represents Lo.

Обычно существует неопределенность как в приводах (входах), так и в датчиках (выходах). Поэтому целесообразно вычислять маржу диска на заводских входах и выходах. Использовать Li = C*P для вычисления маржи на заводских входах. Для этой системы маржа одинакова на заводских входах и выходах.

Li = C*P;
[DMi,MMi] = diskmargin(Li);
MMi

MMi = struct with fields:
           GainMargin: [0.6839 1.4621]
          PhaseMargin: [-21.2607 21.2607]
           DiskMargin: 0.3754
           LowerBound: 0.3754
           UpperBound: 0.3762
            Frequency: 0
    WorstPerturbation: [2x2 ss]

Наконец, можно также вычислить поля многолучевого диска для изменения коэффициента усиления или фазы как на входах, так и на выходах установки. Этот подход является наиболее тщательной оценкой пределов устойчивости, поскольку он учитывает независимые и параллельные изменения усиления или фазы во всех входных и выходных каналах. Как и ожидалось, из всех трех показателей это дает наименьший коэффициент усиления и поля фазы.

MMio = diskmargin(P,C);
diskmarginplot(MMio.GainMargin)

Figure contains an axes. The axes with title Range of gain and phase variations contains 5 objects of type patch, text, line.

Стабильность гарантируется только при изменении коэффициента усиления менее чем на 2 дБ или при изменении фазы менее чем на 13 °. Однако эти изменения происходят на входах и выходах P, так что общее изменение усиления или фазы ввода-вывода в два раза больше.

Чувствительность дисковых полей к увеличению и уменьшению

Открыть сценарий в реальном времени

По умолчанию diskmargin вычисляет запас симметричного усиления с помощью gmin = 1/gmaxи соответствующий запас фазы. Однако в некоторых системах стабильность петли может быть более чувствительной к увеличению или уменьшению усиления в разомкнутом контуре. Использовать параметр перекоса sigma для изучения этой чувствительности.

Вычислите запас диска и связанные с ним коэффициенты усиления и фазы для функции передачи SISO при трех значениях sigma. Отрицательный sigma смещает вычисления в сторону уменьшения коэффициента усиления. Положительный sigma отклонения в сторону увеличения прироста.

L = tf(25,[1 10 10 10]);
DMdec = diskmargin(L,-2);
DMbal = diskmargin(L,0);
DMinc = diskmargin(L,2); 
DGMdec = DMdec.GainMargin

DGMdec = 1×2

    0.4013    1.3745

DGMbal = DMbal.GainMargin

DGMbal = 1×2

    0.6273    1.5942

DGMinc = DMinc.GainMargin

DGMinc = 1×2

    0.7717    1.7247

В совокупности эти результаты показывают, что при отсутствии фазовых изменений стабильность поддерживается для относительных изменений усиления между 0,4 и 1,72. Чтобы увидеть, как фазовый запас зависит от этих изменений усиления, постройте график стабильных диапазонов усиления и фазовых изменений для каждого diskmargin результат.

diskmarginplot([DGMdec;DGMbal;DGMinc])
legend('sigma = -2','sigma = 0','sigma = 2')
title('Stable range of gain and phase variations')

Figure contains an axes. The axes with title Stable range of gain and phase variations contains 3 objects of type patch. These objects represent sigma = -2, sigma = 0, sigma = 2.

Этот график показывает, что контур обратной связи может допускать большие изменения фазы, когда коэффициент усиления уменьшается. Другими словами, стабильность петли более чувствительна к увеличению усиления. Хотя sigma = -2 дает запас фазы до 30 градусов, это большое значение предполагает небольшое увеличение коэффициента усиления менее 3 дБ. Однако график показывает, что при увеличении коэффициента усиления на 4 дБ запас по фазе падает до менее чем 15 градусов. В противоположность этому, он остается больше 30 градусов, когда коэффициент усиления уменьшается на 4 дБ.

Таким образом, варьирование перекоса sigma может дать более полную картину чувствительности к коэффициенту усиления и фазовой неопределенности. Если вы в основном не заинтересованы в изменениях усиления в одном направлении (увеличение или уменьшение), не рекомендуется делать выводы из одного ненулевого значения sigma. Вместо этого используйте значение по умолчанию sigma = 0, чтобы получить несмещенные оценки усиления и полей фазы. При использовании ненулевых значений sigma, используйте как положительные, так и отрицательные значения для сравнения относительной чувствительности к увеличению и уменьшению усиления.

Входные аргументы

свернуть все

`L` - Отклик с разомкнутым контуром
динамическая системная модель | массив модели

Отклик с разомкнутым контуром, заданный как динамическая модель системы. L может быть SISO или MIMO, если он имеет одинаковое количество входов и выходов. diskmargin вычисляет пределы устойчивости диска для системы с отрицательной обратной связью по замкнутому циклу feedback(L,eye(N)).

Diagram of a feedback loop consisting of L with unit negative feedback.

Вычисление полей диска системы положительной обратной связи feedback(L,eye(N),+1), использовать diskmargin(-L).

Когда у вас есть завод P и контроллер C, можно вычислить поля диска для изменений коэффициента усиления (или фазы) на входах или выходах установки, как показано на следующей диаграмме.

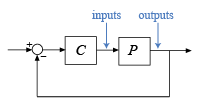
Diagram of a feedback loop consisting of P*C with unit negative feedback, with arrows indicating the inputs and outputs of the plant P.

Для расчета маржи на заводских выходах установите L = P*C.
Для расчета маржи на заводских вводах установите L = C*P.

L может быть непрерывным временем или дискретным временем. Если L является обобщенной государственно-пространственной моделью (genss или uss) затем diskmargin использует текущее или номинальное значение всех блоков проекта управления в L.

Если L является моделью данных частотного отклика (например, frd), то diskmargin вычисляет поля на каждой частоте, представленной в модели. Функция возвращает поля на частоте с наименьшим запасом диска.

Если L является массивом модели, то diskmargin вычисляет поля для каждой модели в массиве.

`P` - Завод
динамическая модель системы

Установка, заданная как динамическая модель системы. P может быть SISO или MIMO, если P*C имеет одинаковое количество входов и выходов. diskmargin вычисляет пределы стабильности на основе дисков для системы с отрицательной обратной связью с замкнутым контуром. Для вычисления дисковых полей системы с положительной обратной связью используйте diskmargin(P,-C).

P может быть непрерывным временем или дискретным временем. Если P является обобщенной государственно-пространственной моделью (genss или uss) затем diskmargin использует текущее или номинальное значение всех блоков проекта управления в P.

Если P является моделью данных частотного отклика (например, frd), то diskmargin вычисляет поля на каждой частоте, представленной в модели. Функция возвращает поля на частоте с наименьшим запасом диска.

`C` - Контроллер
динамическая модель системы

Контроллер, указанный как динамическая модель системы. C может быть SISO или MIMO, если P*C имеет одинаковое количество входов и выходов. diskmargin вычисляет пределы стабильности на основе дисков для системы с отрицательной обратной связью с замкнутым контуром. Для вычисления дисковых полей системы с положительной обратной связью используйте diskmargin(P,-C).

C может быть непрерывным временем или дискретным временем. Если C является обобщенной государственно-пространственной моделью (genss или uss) затем diskmargin использует текущее или номинальное значение всех блоков проекта управления в C.

Если C является моделью данных частотного отклика (например, frd), то diskmargin вычисляет поля на каждой частоте, представленной в модели. Функция возвращает поля на частоте с наименьшим запасом диска.

`sigma` - Перекос
0 (по умолчанию) | вещественный скаляр

Перекос области неопределенности, используемый для вычисления полей стабильности, заданных как действительное скалярное значение. Этот параметр смещает неопределенность, используемую для моделирования усиления и фазовых изменений в сторону увеличения или уменьшения усиления.

Дефолт sigma = 0 использует сбалансированную модель изменения коэффициента усиления в диапазоне [gmin,gmax], с gmin = 1/gmax.
Положительный sigma использует модель с большим увеличением усиления, чем снижением (gmax > 1/gmin).
Отрицательный sigma использует модель с большим снижением усиления, чем увеличением (gmin < 1/gmax).

Использовать значение по умолчанию sigma = 0, чтобы получить несмещенные оценки усиления и полей фазы. Можно проверить относительную чувствительность для увеличения и уменьшения усиления, сравнивая полученные поля с положительными и отрицательными sigma значения. Пример см. в разделе Чувствительность полей на основе дисков для увеличения и уменьшения. Для получения более подробной информации о выборе sigma влияет на расчет запаса, см. раздел Анализ стабильности с использованием полей диска.

Выходные аргументы

свернуть все

`DM` - Дисковые поля для каждого канала обратной связи
структура | массив структуры

Дисковые поля для каждого канала обратной связи со всеми остальными контурами закрыты, возвращены как структура для циклов обратной связи SISO или массив N-by-1 структуры для цикла MIMO с N каналами обратной связи. Поля DM(i) являются:

Область	Стоимость
`GainMargin`	Дисковые поля усиления соответствующего канала обратной связи, возвращаемые как вектор формы `[gmin,gmax]`. Эти значения выражают в абсолютных единицах величину, на которую коэффициент усиления контура в этом канале может уменьшаться или увеличиваться при сохранении стабильности. Например, если `DM(i).GainMargin = [0.8,1.25]` тогда усиление i-ой петли можно умножить на любой коэффициент между 0,8 и 1,25, не вызывая нестабильности. Когда `sigma` = 0, `gmin = 1/gmax`. Если усиление с разомкнутым контуром может изменить знак без потери устойчивости, `gmin` может быть меньше нуля для достаточно больших отрицательных `sigma`. Если номинальная система замкнутого контура нестабильна, то `DM(i).GainMargin = [1 1]`.
`PhaseMargin`	Дисковый запас фазы соответствующего канала обратной связи, возвращаемый как вектор формы `[-pm,pm]` в градусах. Эти значения выражают величину, на которую фаза контура в этом канале может уменьшаться или увеличиваться при сохранении стабильности. Если система с замкнутым контуром нестабильна, то `DM(i).PhaseMargin = [0 0]`.
`DiskMargin`	Максимальная ɑ, совместимая со стабильностью по замкнутому контуру для соответствующего канала обратной связи. ɑ параметризует неопределенность в отклике цикла (см. Алгоритмы). Если система с замкнутым контуром нестабильна, то `DM(i).DiskMargin = 0`.
`LowerBound`	Нижняя граница на поле диска. Это значение совпадает с `DiskMargin`.
`UpperBound`	Верхняя граница на поле диска. Это значение представляет собой верхний предел фактического дискового запаса системы. Другими словами, запас диска гарантированно не хуже `LowerBound` и не лучше, чем `UpperBound`.
`Frequency`	Частота, при которой возникает самый слабый запас для соответствующего канала петли. Это значение в рад/`TimeUnit`, где `TimeUnit` является `TimeUnit` имущество `L`.
`WorstPerturbation`	Наименьшее усиление и изменение фазы, которое приводит к нестабильной петле обратной связи, возвращаемой как состояние-пространство (`ss`) модель с N входами и выходами, где N - количество входов и выходов в `L`. Система `F(s) = WorstPerturbation` является таким, что следующий контур обратной связи является немного устойчивым, с полюсом на границе устойчивости на частоте `DM(i).Frequency`. Эта модель состояния-пространства является диагональным возмущением формы `F(s) = diag(f1(s),...,fN(s))`. Каждый `fj(s)` - динамическая система с реальным параметром, которая реализует наихудший случай комплексного усиления и изменения фазы, применяемый к каждому каналу контура обратной связи. Для запаса времени цикла в момент времени k-го цикла обратной связи, только k-й элемент `fk(s)` из `DM(k).WorstPerturbation` отличается от единства. Для получения дополнительной информации по интерпретации `WorstPerturbation`, см. раздел Запас диска и наименьшее дестабилизирующее возмущение При анализе линейной аппроксимации нелинейной системы может быть полезно вводить `WorstPerturbation` в нелинейное моделирование для дальнейшего анализа дестабилизирующего воздействия этого наихудшего случая усиления и изменения фазы. Пример см. в разделе Надежный контроллер MIMO для двухконтурного автопилота.

Когда L = P*C - отклик системы с разомкнутым контуром, содержащей контроллер и установку с отрицательной обратной связью блока в каждом канале, DM содержит пределы устойчивости для вариаций на выходе установки. Чтобы рассчитать пределы устойчивости для изменений на заводских вводах, используйте L = C*P. Для расчета пределов устойчивости для одновременных независимых вариаций как на заводских входах, так и на выходах используйте MMIO = diskmargin(P,C).

Когда L является массивом модели, DM имеет дополнительные размеры, соответствующие размерам массива L. Например, если L является массивом 1 на 3 моделей с двумя входами и двумя выходами, затем DM является массивом структуры 2 на 3. DM(j,k) содержит поля для j-го канала обратной связи k-ой модели в массиве.

`MM` - Поля многолучевого диска
структура

Поля многолучевого диска, возвращенные в виде структуры. Поля усиления (или фазы) количественно определяют, насколько изменение усиления (или изменение фазы) система может выдерживать во всех каналах обратной связи одновременно, оставаясь стабильной. Таким образом, MM представляет собой единую структуру независимо от количества каналов обратной связи в системе. (Для систем SISO, MM = DM.) Поля MM являются:

Область	Стоимость
`GainMargin`	Поля усиления на основе многолучевого диска, возвращаемые как вектор формы `[gmin,gmax]`. Эти значения выражают в абсолютных единицах величину, на которую коэффициент усиления контура может изменяться во всех каналах независимо и одновременно при сохранении стабильности. Например, если `MM.GainMargin = [0.8,1.25]` тогда усиление всех контуров можно умножить на любой коэффициент между 0,8 и 1,25, не вызывая нестабильности. Когда `sigma` = 0, `gmin = 1/gmax`.
`PhaseMargin`	Поле фазы на основе многолучевого диска, возвращаемое как вектор формы `[-pm,pm]` в градусах. Эти значения выражают величину, на которую фаза контура может изменяться во всех каналах независимо и одновременно при сохранении стабильности.
`DiskMargin`	Максимальная ɑ, совместимая со стабильностью по замкнутому контуру. ɑ параметризует неопределенность в отклике цикла (см. Алгоритмы).
`LowerBound`	Нижняя граница на поле диска. Это значение совпадает с `DiskMargin`.
`UpperBound`	Верхняя граница на поле диска. Это значение представляет собой верхний предел фактического дискового запаса системы. Другими словами, запас диска гарантированно не хуже `LowerBound` и не лучше, чем `UpperBound`.
`Frequency`	Частота, при которой возникает самый слабый запас. Это значение в рад/`TimeUnit`, где `TimeUnit` является `TimeUnit` имущество `L`.
`WorstPerturbation`	Наименьшее усиление и изменение фазы, которое приводит к нестабильной петле обратной связи, возвращаемой как состояние-пространство (`ss`) модель с N входами и выходами, где N - количество входов и выходов в `L`. Система `F(s) = WorstPerturbation` является таким, что следующий контур обратной связи является немного устойчивым, с полюсом на границе устойчивости при `MM.Frequency`. Эта модель состояния-пространства является диагональным возмущением формы `F(s) = diag(f1(s),...,fN(s))`. Каждый `fj(s)` - динамическая система с реальным параметром, которая реализует наихудший случай комплексного усиления и изменения фазы, применяемый к каждому каналу контура обратной связи. Для получения дополнительной информации по интерпретации `WorstPerturbation`, см. раздел Запас диска и наименьшее дестабилизирующее возмущение При анализе линейной аппроксимации нелинейной системы может быть полезно вводить `WorstPerturbation` в нелинейное моделирование для дальнейшего анализа дестабилизирующего воздействия этого наихудшего случая усиления и изменения фазы. Пример см. в разделе Надежный контроллер MIMO для двухконтурного автопилота.

Когда L = P*C - отклик системы с разомкнутым контуром, содержащей контроллер и установку с отрицательной обратной связью блока в каждом канале, MM содержит пределы устойчивости для вариаций на выходе установки. Чтобы рассчитать пределы устойчивости для изменений на заводских вводах, используйте L = C*P. Для расчета пределов устойчивости для одновременных независимых вариаций как на заводских входах, так и на выходах используйте MMIO = diskmargin(P,C).

Когда L является массивом модели, MM является массивом структуры с одной записью для каждой модели в L.

`MMIO` - Дисковые поля для независимых вариаций всех входных и выходных каналов
структура

Дисковые поля для независимых вариаций, применяемые одновременно на входном и выходном каналах установки P, возвращенный как структура, имеющая те же поля, что и MM.

Для вариаций, применяемых одновременно на входах и выходах, WorstPerturbation поле само по себе является структурой с полями Input и Output. Каждое из этих полей содержит модель пространства состояний, такую, что для Fi(s) = MMIO.WorstPerturbation.Input и Fo(s) = MMIO.WorstPerturbation.Output, система следующей диаграммы является незначительно нестабильной, с полюсом на границе устойчивости на частоте MMIO.Frequency.

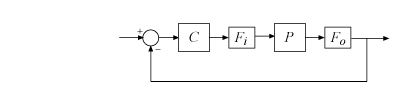
Diagram of a feedback loop consisting of Fo*P*Fi*C with unit negative feedback.

Эти модели пространства состояний Input и Output - диагональные возмущения вида F(s) = diag(f1(s),...,fN(s)). Каждый fj(s) - динамическая система с реальным параметром, которая реализует наихудший случай комплексного усиления и изменения фазы, применяемый к каждому каналу контура обратной связи.

Совет

diskmargin предполагает отрицательную обратную связь. Для вычисления полей диска системы положительной обратной связи используйте diskmargin(-L) или diskmargin(P,-C).
Для вычисления полей диска для системы, смоделированной в Simulink ®, сначала выполните линеаризацию модели, чтобы получить отклик с разомкнутым контуром в определенной рабочей точке. Затем используйтеdiskmargin для вычисления пределов устойчивости для линеаризованной системы. Дополнительные сведения см. в разделе Поля стабильности модели Simulink.
Для вычисления классического усиления и полей фаз используйте allmargin.
Можно визуализировать поля диска с помощью diskmarginplot.

Алгоритмы

свернуть все

diskmargin вычисляет коэффициент усиления и фазовые поля, применяя основанную на дисках модель неопределенности для представления коэффициента усиления и фазовых изменений, и затем находит самый большой такой диск, для которого система с замкнутым контуром является стабильной.

Модель усиления и фазовой неопределенности

Для SISO L модель неопределенности для анализа запаса диска включает мультипликативную комплексную неопределенность F в функцию передачи цикла следующим образом:

$\frac{}{} F=1+α[(1-σ)/2]δ1-α[(1+σ)/2]δ.$

Здесь,

δ - динамическая неопределенность, ограниченная коэффициентом усиления, нормализованная таким образом, что она всегда изменяется в пределах единичного диска (| δ | < 1).
α задает величину усиления и изменения фазы, смоделированную F. Для фиксированного λ параметр ɑ управляет размером диска. Для α = 0 мультипликативный коэффициент равен 1, что соответствует номинальному L.
, называемый перекосом, смещает смоделированную неопределенность в сторону увеличения или уменьшения усиления. (Дополнительные сведения о влиянии перекоса на модель неопределенности см. в разделе Анализ стабильности с использованием полей диска.)

Для систем MIMO модель позволяет независимо изменять неопределенность в каждом канале:

$_{Fj} \frac{= 1 + α [(1 -_{}}{_{}}$

Модель заменяет ответ L с разомкнутым контуром MIMO на L * F, где

$F = \begin{matrix} _{(} \\ _{} \end{matrix} F1000⋱000FN$ ).

Дисковые вычисления

Для данного sigma, запас диска является наибольшим ɑ, для которого система с замкнутым контуром feedback(L*F,1) (или feedback(L*F,eye(N)) для систем MIMO) является стабильным для всех значений F. Чтобы найти это значение, diskmargin решает проблему надежной стабильности: Найдите наибольший α, такой, чтобы система с замкнутым контуром была стабильной для всех F в диске неопределенности Δ (α, λ), описанном

$\frac{}{} Δ(α,σ)={F=1+α[(1-σ)/2]δ1-α[(1+σ)/2]δ : |δ|<1}.$

В случае SISO надежный анализ устойчивости приводит к

$_{} {\frac{}{αmax=‖1S+ (λ - 1}}_{})/$ 2‖∞,

где S - функция чувствительности (1 + L) ^-1 .

В случае MIMO надежный анализ стабильности приводит к

$_{αmax} \frac{=}{_{} 1 мкΔ \frac{(S + (}{λ}} -$ 1) I2).

Здесь мкΔ - структурированное сингулярное значение (mussv) для диагональной структуры

$Δ = \begin{matrix} _{(} \\ _{} \end{matrix} δ1000⋱000δN$ ),

и _δj - нормализованная неопределенность для каждого _Fj.

Для получения дополнительной информации о расчете маржи см. [2].

Вопросы совместимости

развернуть все

Диапазон коэффициента усиления на основе дисков может включать отрицательный коэффициент усиления

В R2020a изменилось поведение

diskmargin возвращает поля усиления на основе диска в GainMargin поле его выходных структур DM, MM, и MMIO. Эти поля имеют вид [gmin,gmax], что означает, что коэффициент усиления с разомкнутым контуром может быть умножен на любой коэффициент в этом диапазоне без потери стабильности с замкнутым контуром. Начиная с R2020a, нижний конец диапазона gmin может быть отрицательным для некоторых отрицательных значений перекоса sigmaесли система с замкнутым контуром остается стабильной, даже если изменяется признак усиления с разомкнутым контуром. Перекос управляет смещением запаса усиления на основе диска в сторону уменьшения или увеличения коэффициента усиления (см. Анализ стабильности с использованием полей диска). Ранее диапазон усиления-запаса всегда был положительным.

Ссылки

[1] Блайт, Джеймс Д., Р. Лейн Дейли и Дагфинн Гангсаас. «Практическое проектирование закона контроля для летательных аппаратов с использованием многовариантных методов». Международный журнал контроля 59, № 1 (январь 1994 года): 93-137. https://doi.org/10.1080/00207179408923071.

[2] Зайлер, Питер, Эндрю Паккард и Паскаль Гахинет. «Введение в поля диска [примечания к лекциям]». Журнал систем управления IEEE 40, № 5 (октябрь 2020): 78-95.

См. также

allmargin | diskmarginplot | margin | wcdiskmargin

Темы

Представлен в R2018b

Документация

diskmargin

Синтаксис

Описание

Примеры

Границы диска контура обратной связи MIMO

Чувствительность дисковых полей к увеличению и уменьшению

Входные аргументы

`L` - Отклик с разомкнутым контуром
динамическая системная модель | массив модели

`P` - Завод
динамическая модель системы

`C` - Контроллер
динамическая модель системы

`sigma` - Перекос
0 (по умолчанию) | вещественный скаляр

Выходные аргументы

`DM` - Дисковые поля для каждого канала обратной связи
структура | массив структуры

`MM` - Поля многолучевого диска
структура

`MMIO` - Дисковые поля для независимых вариаций всех входных и выходных каналов
структура

Совет

Алгоритмы

Модель усиления и фазовой неопределенности

Дисковые вычисления

Вопросы совместимости

Диапазон коэффициента усиления на основе дисков может включать отрицательный коэффициент усиления

Ссылки

См. также

Темы

Документация по инструментам надежного управления

Поддержка

Документация

diskmargin

Синтаксис

Описание

Примеры

Границы диска контура обратной связи MIMO

Чувствительность дисковых полей к увеличению и уменьшению

Входные аргументы

L - Отклик с разомкнутым контуром динамическая системная модель | массив модели

P - Завод динамическая модель системы

C - Контроллер динамическая модель системы

sigma - Перекос 0 (по умолчанию) | вещественный скаляр

Выходные аргументы

DM - Дисковые поля для каждого канала обратной связи структура | массив структуры

MM - Поля многолучевого диска структура

MMIO - Дисковые поля для независимых вариаций всех входных и выходных каналов структура

Совет

Алгоритмы

Модель усиления и фазовой неопределенности

Дисковые вычисления

Вопросы совместимости

Диапазон коэффициента усиления на основе дисков может включать отрицательный коэффициент усиления

Ссылки

См. также

Темы

Документация по инструментам надежного управления

Поддержка

`L` - Отклик с разомкнутым контуром
динамическая системная модель | массив модели

`P` - Завод
динамическая модель системы

`C` - Контроллер
динамическая модель системы

`sigma` - Перекос
0 (по умолчанию) | вещественный скаляр

`DM` - Дисковые поля для каждого канала обратной связи
структура | массив структуры

`MM` - Поля многолучевого диска
структура

`MMIO` - Дисковые поля для независимых вариаций всех входных и выходных каналов
структура