nyquist

Найквистский график частотной характеристики

Синтаксис

nyquist(sys) nyquist(sys,w) nyquist(sys1,sys2,...,sysN) nyquist(sys1,sys2,...,sysN,w) nyquist(sys1,'PlotStyle1',...,sysN,'PlotStyleN') [re,im,w] = nyquist(sys) [re,im] = nyquist(sys,w) [re,im,w,sdre,sdim] = nyquist(sys)

Описание

nyquist создает график Найквиста частотной характеристики динамической системной модели. При вызове без левых аргументов nyquist создает график Найквиста на экране. Графики Nyquist используются для анализа свойств системы, включая запас усиления, запас фазы и стабильность.

nyquist(sys) создает график Nyquist динамической системы sys. Эта модель может быть непрерывной или дискретной, а также SISO или MIMO. В случае MIMO nyquist создает массив графиков Найквиста, каждый график показывает отклик одного конкретного канала ввода-вывода. Точки частоты выбираются автоматически на основе системных полюсов и нулей.

nyquist(sys,w) явно указывает диапазон частот или точки частот, используемые для графика. Чтобы сосредоточиться на определенном частотном интервале, установите w = {wmin,wmax}. Для использования определенных частотных точек установите w к вектору требуемых частот. Использовать logspace формируют логарифмически разнесенные частотные векторы. Частоты должны быть в rad/TimeUnit, где TimeUnit - единицы времени входной динамической системы, указанные в TimeUnit имущество sys.

nyquist(sys1,sys2,...,sysN) или nyquist(sys1,sys2,...,sysN,w) накладывает найквистовские графики нескольких моделей LTI на одну фигуру. Все системы должны иметь одинаковое количество входов и выходов, но в противном случае они могут представлять собой сочетание систем непрерывного и дискретного времени. Можно также указать отличительный цвет, стиль линий и/или маркер для каждого системного графика с помощью синтаксиса. nyquist(sys1,'PlotStyle1',...,sysN,'PlotStyleN').

[re,im,w] = nyquist(sys) и [re,im] = nyquist(sys,w) возврат действительной и мнимой частей частотной характеристики на частотах w (в rad/TimeUnit). re и im являются 3-D массивами (подробные сведения см. в разделе «Аргументы» ниже).

[re,im,w,sdre,sdim] = nyquist(sys) также возвращает стандартные отклонения re и im для идентифицированной системы sys.

Аргументы

Выходные аргументы re и im 3-D массивы с размерами

$(количество выходов) \times (количество входов) \times (длина w)$

Для систем SISO скаляры re(1,1,k) и im(1,1,k) представляют собой действительную и мнимую части отклика на частоте λ k = w (k).

$\begin{array}{l} re (1,1, k) = Re_{(} h \\ (jü k)) im (1,1, k_{)} = \end{array}$ Im (h (jwk))

Для систем MIMO с передаточной функцией H (s ),re(:,:,k) и im(:,:,k) дать действительную и мнимую части H (_jstartk) (оба массива имеют столько строк, сколько выходов, и столько столбцов, как входов). Таким образом ,

$\begin{array}{l} re (i, j, k) = {Re}_{(} {hij}_{} ( \\ jü k)) im (i, j, k)_{=} {Im}_{} ( \end{array}$ hij (jü k))

где _hij - передаточная функция от входа j к выходу i.

Примеры

свернуть все

График динамической системы Найквиста

Открыть сценарий в реальном времени

Создайте следующую передаточную функцию и постройте график ее ответа Nyquist.

$H (s) \frac{=^{} 2s2 +}{^{} 5s +}$ 1s2 + 2s + 3.

H = tf([2 5 1],[1 2 3]);
nyquist(H)

Figure contains an axes. The axes contains 2 objects of type line. This object represents H.

nyquist функция может отображать сетку из M-кругов, которые являются контурами постоянной величины замкнутого контура. M-круги определяются как локус комплексных чисел, где следующая величина является постоянным значением на частоте.

$T (jλ) \frac{= | G}{(jλ) 1}$ + G (jλ) |.

В данном случае λ - частота в радианах/TimeUnit, где TimeUnit - системные единицы времени, а G - совокупность комплексных чисел, удовлетворяющих требованию постоянной величины.

Для отображения сетки M-кругов щелкните правой кнопкой мыши на графике и выберите «Сетка». В качестве альтернативы используйте grid команда.

grid on

Figure contains an axes. The axes contains 2 objects of type line. This object represents H.

Создание графика Найквиста идентифицированной модели с неопределенностью ответа

В этом примере используются:

Панель инструментов идентификации системы

Открыть сценарий в реальном времени

Вычислите стандартные отклонения действительной и мнимой частей частотной характеристики идентифицированной модели. Используйте эти данные, чтобы создать график неопределенности отклика на уровне 3λ.

Данные оценки нагрузки z2.

load iddata2 z2;

Определите модель передаточной функции с помощью данных.

sys_p = tfest(z2,2);

Получение стандартных отклонений для действительной и мнимой частей частотной характеристики для набора 512 частот, w.

w = linspace(-10*pi,10*pi,512);
[re,im,wout,sdre,sdim] = nyquist(sys_p,w);

Здесь re и im являются действительной и мнимой частями частотной характеристики, и sdre и sdim являются их стандартными отклонениями соответственно. Частоты в wout совпадают с частотами, указанными в w.

Создайте график Найквиста, показывающий отклик и его неопределённость 3λ.

re = squeeze(re);
im = squeeze(im); 
sdre = squeeze(sdre);
sdim = squeeze(sdim);
plot(re,im,'b',re+3*sdre,im+3*sdim,'k:',re-3*sdre,im-3*sdim,'k:')
xlabel('Real Axis');
ylabel('Imaginary Axis');

Figure contains an axes. The axes contains 3 objects of type line.

Совет

Можно изменить свойства графика, например единицы измерения. Сведения о способах изменения свойств графиков см. в разделе Способы настройки графиков. Для максимальной гибкости настройки свойств печати используйте nyquistplot команда вместо nyquist.
В контекстном меню доступны две опции зумирования, которые применяются специально к графикам Найквиста:
- Полный вид (Full View) - закрепляет неограниченные ветви графика Найквиста, но по-прежнему включает критическую точку (-1, 0).
- Зумирование (-1,0) - зумирование вокруг критической точки (-1,0). (Чтобы получить программный доступ к масштабированию критических точек, используйте nyquistplot вместо этого.)
Чтобы активировать маркеры данных, отображающие вещественные и мнимые значения с заданной частотой, щелкните в любом месте кривой. На следующем рисунке показан nyquist печать с маркером данных.

Алгоритмы

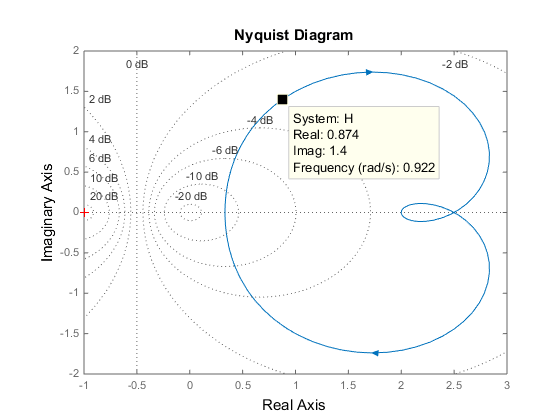
Посмотрите bode.

См. также

Представлен до R2006a

Документация