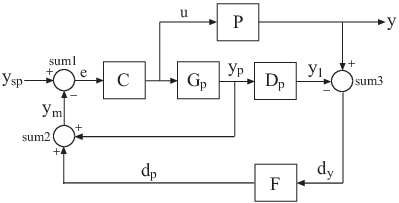
В этом примере показано, как построить произвольную блок-схему путем соединения моделей с помощью connect. Система представляет собой предсказатель Смита, систему управления с одним входом и одним выходом (SISO), показанную на следующей блок-схеме.
Дополнительные сведения о предикторе Смита см. в разделе Управление процессами с длительным временем покоя: предиктор Смита.
connect команда позволяет создать общую передаточную функцию от ysp до y. Использовать connect, укажите имена входных и выходных каналов компонентов блок-схемы. connect автоматически соединяет порты с тем же именем, как показано на следующем рисунке.

Чтобы построить модель замкнутого цикла системы предсказателя Смита от ysp до y:
Создание компонентов блок-схемы модели процесса P, модель предиктора Gp, модель задержки Dp, фильтр Fи контроллер PI C. Укажите имена входных и выходных каналов каждой модели, чтобы connect может автоматически присоединяться к ним для построения блок-схемы.
s = tf('s');
P = exp(-93.9*s) * 5.6/(40.2*s+1);
P.InputName = 'u'; P.OutputName = 'y';
Gp = 5.6/(40.2*s+1);
Gp.InputName = 'u'; Gp.OutputName = 'yp';
Dp = exp(-93.9*s);
Dp.InputName = 'yp'; Dp.OutputName = 'y1';
F = 1/(20*s+1);
F.InputName = 'dy'; F.OutputName = 'dp';
C = pidstd(0.574,40.1);
C.Inputname = 'e'; C.OutputName = 'u';Создайте суммирующие соединения, необходимые для завершения блок-схемы.
sum1 = sumblk('e = ysp - ym');
sum2 = sumblk('ym = yp + dp');
sum3 = sumblk('dy = y - y1');Аргумент для sumblk - формула, которая связывает входной и выходной сигналы суммирующего перехода. sumblk создает суммирующий переход с именами входного и выходного сигналов, указанными в формуле. Например, в sum1, формула 'e = ysp - ym' задает выходной сигнал с именем e, которая является разницей между входными сигналами ysp и ym.
Соберите полную модель от ysp до y.
T = connect(P,Gp,Dp,C,F,sum1,sum2,sum3,'ysp','y');
Можно перечислить модели и суммирующие соединения в любом порядке, потому что connect автоматически связывает их с использованием имен входных и выходных каналов.
Последние два аргумента определяют входной и выходной сигналы многоконтурной структуры управления. Таким образом, T является ss модель с входными данными ysp и выходные данные y.