В этом примере показано, как построить систему управления MIMO с помощью connect для соединения числовых моделей LTI и настраиваемых блоков проектирования элементов управления.
Рассмотрим следующую систему управления с двумя входами и двумя выходами.
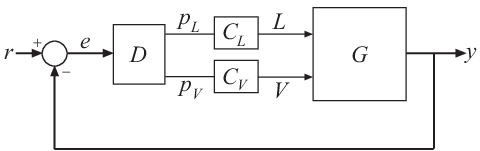
Установка G представляет собой дистилляционную колонну с двумя входами и двумя выходами. Двумя входами являются рефлюкс L и кипячение V. Двумя выходами являются концентрации двух химических веществ, представленные векторным сигналом y = [y1, y2]. Эту модель завода можно представить следующим образом:
− 109,6].
Сигнал векторной уставки r = [r1, r2] определяет требуемые концентрации двух химических веществ. Сигнал векторной ошибки e представляет собой входной сигнал D, статическую матрицу разъединения 2 на 2. CL и CV представляют независимые контроллеры PI, которые управляют двумя входами G .
Для создания модели с двумя входами и двумя выходами, представляющей эту систему управления с замкнутым контуром:
Создайте числовую модель LTI, представляющую завод 2 на 2 G.
s = tf('s','TimeUnit','minutes');
G = [87.8 -86.4 ; 108.2 -109.6]/(75*s+1);
G.InputName = {'L','V'};
G.OutputName = 'y';
При построении модели с замкнутым контуром connect использует входные и выходные имена для формирования соединений между компонентами блок-схемы. Поэтому необходимо присвоить имена входам и выходам передаточной функции. G одним из следующих способов:.
Можно назначить имена ввода и вывода отдельным сигналам, указав имена сигналов в массиве ячеек, как в разделе G.InputName = {'L','V'}
Кроме того, можно использовать векторное именование сигналов, которое автоматически расширяется программой. Например, команда G.OutputName = 'y' присваивает имена 'y(1)' и 'y(2)' к выводам G.
Создайте настраиваемые блоки конструкции управления, представляющие матрицу разъединения D и контроллеры PI CL и CV.
D = tunableGain('Decoupler',eye(2));
D.u = 'e';
D.y = {'pL','pV'};
C_L = tunablePID('C_L','pi'); C_L.TimeUnit = 'minutes';
C_L.u = 'pL'; C_L.y = 'L';
C_V = tunablePID('C_V','pi'); C_V.TimeUnit = 'minutes';
C_V.u = 'pV'; C_V.y = 'V';Примечание
u и y являются краткими обозначениями для InputName и OutputName соответственно. Таким образом, например, вводится:
D.u = 'e';
D.y = {'pL','pV'};эквивалентно введению:
D.InputName = 'e';
D.OutputName = {'pL','pV'};Создайте суммирующее соединение.
Суммирующий переход формирует сигналы ошибки e, принимая разность между r и y.
Sum = sumblk('e = r - y',2);Sum представляет передаточную функцию для суммирующего перехода, описанного формулой 'e = r - y'. Второй аргумент для sumblk указывает, что входы и выходы Sum - каждый векторный сигнал длиной 2. Поэтому программное обеспечение автоматически присваивает имена сигналов {'r(1)','r(2)','y(1)','y(2)'} кому Sum.InputName и {'e(1)','e(2)'} кому Sum.OutputName.
Соедините все компоненты для построения системы с замкнутым контуром от r до y.
CLry = connect(G,D,C_L,C_V,Sum,'r','y');
Аргументы для connect функция включает все компоненты системы с замкнутым контуром в любом порядке. connect автоматическое объединение компонентов с использованием входных и выходных имен для объединения сигналов.
Последние два аргумента для connect укажите выходной и входной сигналы модели с замкнутым контуром соответственно. Получающееся genss модель CLry имеет два входа и два выхода.