Построение и работа со сплайнами ppform

Построение ppform

Кусочно-многочлен обычно строится некоторой командой, посредством процесса интерполяции или аппроксимации, или преобразования из какой-либо другой формы, например из В-формы, и выводится как переменная. Но также можно составить один с нуля, используя утверждение

pp
= ppmak(breaks,coefs)

Например, при вводе pp=ppmak(-5:-1,-22:-11), или, более явно,

breaks = -5:-1;
coefs = -22:-11; pp = ppmak(breaks,coefs);

задается равномерная последовательность разрывов -5:-1 и последовательность коэффициентов -22:-11. Поскольку эта последовательность разбиения имеет 5 записей, следовательно, 4 интервала разбиения, в то время как последовательность коэффициентов имеет 12 записей, фактически задается кусочно-многочлен порядка 3 (= 12/4). Команда

fnbrk(pp)

распечатывает все составные части этого кусочно-многочлена следующим образом:

breaks(1:l+1)
    -5 -4 -3 -2 -1  
coefficients(d*l,k)
     -22 -21 -20
     -19 -18 -17
     -16 -15 -14 
     -13 -12 -11
  pieces number l
    4 
order k 
  3 
dimension d of target
    1

Далее, fnbrk может использоваться для отдельной поставки каждой из этих деталей. Однако функциональная возможность «Фитинг кривой» (Curve Fitting) Toolbox™ «Сплайн» (Spline) заключается в том, что обычно не нужно беспокоиться об этих деталях. Вы просто используете pp в качестве аргумента для команд, которые вычисляют, дифференцируют, интегрируют, преобразуют или строят кусочно-полином, описание которого содержится в pp.

Работа со сплайнами ppform

Вот некоторые функции для операций, которые можно выполнить с кусочно-многочленом.

`v = fnval(pp,x)`	Оценивает
`dpp = fnder(pp)`	Дифференцируется
`dirpp = fndir(pp,dir)`	Дифференцирует в направлении `dir`
`ipp = fnint(pp)`	Объединяется
`fnmin(pp,[a,b])`	Поиск минимального значения в заданном интервале
`fnzeros(pp,[a,b])`	Поиск нулей в заданном интервале
`pj = fnbrk(pp,j)`	Выдергивает `j`Часть th-го полинома
`pc = fnbrk(pp,[a b])`	Ограничивает/расширяет интервал [`a`..`b`]
`po = fnxtr(pp,order)`	Выходит за пределы основного интервала по многочлену указанного порядка
`fnplt(pp,[a,b])`	Графики на заданном интервале
`sp = fn2fm(pp,'B-')`	Преобразует в B-форму
`pr = fnrfn(pp,morebreaks)`	Вставка дополнительных разрывов

Вставка дополнительных разрывов удобна, если требуется добавить два кусочно-многочлена с различными разрывами, как это делается в команде fncmb.

Пример ppform

Выполните следующие команды для создания и печати конкретного кусочно-полинома (ppform), описанного в разделе Создание ppform.

Создание кусочно-полинома с последовательностью разрыва -5:-1 и последовательность коэффициентов -22:-11:
```
pp=ppmak(-5:-1,-22:-11)
```

Создайте базовый график:

x = linspace(-5.5,-.5,101);
plot(x, fnval(pp,x),'x')

Добавьте линии разрыва на график:

breaks=fnbrk(pp,'b'); yy=axis; hold on
for j=1:fnbrk(pp,'l')+1
   plot(breaks([j j]),yy(3:4))
end

Наложите график многочлена, который предоставляет третью часть многочлена:
```
plot(x,fnval(fnbrk(pp,3),x),'linew',1.3)
set(gca,'ylim',[-60 -10]), hold off 
```

Кусочно-полиномиальная функция, ее разрывы и полином, дающий свою третью часть

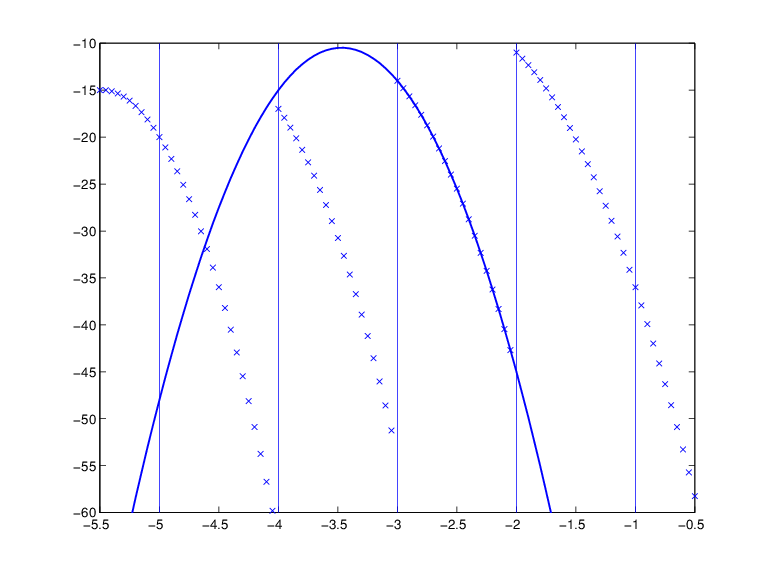
Рисунок выше - окончательная картина. Он показывает кусочно-многочлен как последовательность точек и, солидно поверх него, многочлен, из которого взята его третья часть многочлена. Довольно заметно, что значение кусочно-многочлена при разрыве является его пределом справа, и что значение кусочно-многочлена за пределами его основного интервала получается продлением его крайней левой, соответственно самой правой, многочленовой части.

Хотя ppform кусочно-многочлена эффективен для оценки, построение кусочно-многочлена из некоторых данных обычно более эффективно обрабатывается путем определения сначала его B-формы, то есть его представления в виде линейной комбинации B-сплайнов.

Документация