Если библиотека панели инструментов не содержит нужного параметрического уравнения, можно создать собственное пользовательское уравнение. Библиотечные модели, однако, дают наилучший шанс для быстрой конвергенции. Это потому, что:
Для большинства библиотечных моделей панель инструментов вычисляет оптимальные начальные точки коэффициентов по умолчанию. Для пользовательских моделей панель инструментов выбирает случайные начальные точки по умолчанию для интервала [0,1]. Необходимо найти подходящие начальные точки для пользовательских моделей.
Библиотечные модели используют аналитический якобиан. Пользовательские модели используют конечную разностность.
Можно создать пользовательские общие уравнения с типом посадки «Пользовательское уравнение». Общие модели - это нелинейные комбинации (возможно, нелинейных) терминов. Они определяются уравнениями, которые могут быть нелинейными в параметрах. Пользовательское уравнение подгонки использует нелинейную процедуру подгонки методом наименьших квадратов.
Можно определить пользовательское линейное уравнение, используя тип посадки Пользовательское уравнение (Custom Equation fit), хотя нелинейный фитинг менее эффективен и обычно медленнее линейного фитинга с наименьшими квадратами.
Если вы не знаете, можно ли выразить уравнение как набор линейных функций, то выберите Custom Equation. Может потребоваться поиск подходящих начальных точек.
Если требуется линейный фитинг методом наименьших квадратов для пользовательских уравнений, выберите Linear Fitting вместо этого тип модели. См. раздел Пользовательский линейный фитинг.
В приложении «Фитинг кривой» выберите Custom Equation из списка типов модели.
Используйте пользовательское уравнение для определения собственных уравнений. Пример пользовательского уравнения появляется, если выбрать Пользовательское уравнение (Custom Equation) из списка, как показано здесь для данных кривой.
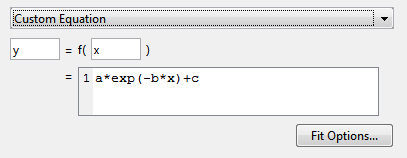
При наличии данных поверхности в примере пользовательского уравнения используются значения x и y.
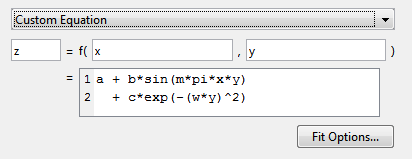
Можно редактировать x, y, и z к любым допустимым именам переменных.
В нижнем поле отредактируйте пример, чтобы определить собственное пользовательское уравнение. Можно ввести любое допустимое выражение MATLAB ® в терминах имен переменных. Можно указать имя функции или сценария (см. раздел «Подгонка кривой, определенной файлом» в приложении «Подгонка кривой»).
Нажмите кнопку «Параметры подгонки», чтобы указать начальные точки или границы. По умолчанию начальные значения выбираются случайным образом на интервале [0,1] и не ограничиваются. Может потребоваться поиск подходящих начальных точек и границ. Пример см. в разделе Пользовательский нелинейный анализ данных ENSO.
Если задать параметры подгонки, а затем изменить другие параметры подгонки, приложение запомнит ваши варианты выбора нижней и верхней границ и начальных точек, если это возможно. Для пользовательских уравнений приложение «Аппроксимация кривой» всегда запоминает пользовательские значения, но для многих библиотечных моделей при изменении настроек аппроксимации приложение автоматически вычисляет новые наилучшие значения для начальных точек или нижних границ.
Пользовательские уравнения можно сохранить как часть сохраненных сеансов приложения «Фитинг кривой».
Функция может выполняться несколько раз как во время фитинга, так и во время предварительной обработки перед фитингом. Помните, что это может занять много времени, если вы используете функции с побочными эффектами, такими как запись данных в файл или отображение диагностической информации в окне команд.
Примеры см. в разделе:
В этом примере показано, как указать имя функции или сценария в качестве модели фитинга в приложении «Фитинг кривой». Определите функцию в файле и используйте ее для подгонки кривой.
Определите функцию в файле MATLAB.
function y = piecewiseLine(x,a,b,c,d,k) % PIECEWISELINE A line made of two pieces % that is not continuous. y = zeros(size(x)); % This example includes a for-loop and if statement % purely for example purposes. for i = 1:length(x) if x(i) < k, y(i) = a + b.* x(i); else y(i) = c + d.* x(i); end end end
Сохраните файл по пути MATLAB.
Определите некоторые данные и откройте приложение «Фитинг кривой».
x = [0.81;0.91;0.13;0.91;0.63;0.098;0.28;0.55;... 0.96;0.96;0.16;0.97;0.96]; y = [0.17;0.12;0.16;0.0035;0.37;0.082;0.34;0.56;... 0.15;-0.046;0.17;-0.091;-0.071]; cftool
В приложении «Фитинг кривой» выберите x и y в списках данных X и Y.
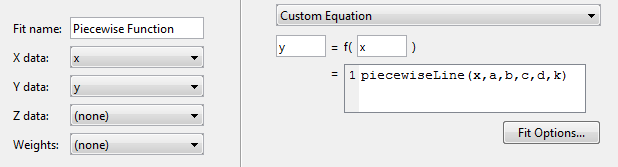
Используйте ваш piecewiseLine в приложении «Фитинг кривой» выберите тип аппроксимации «Пользовательская формула», а затем введите выражение функции в текстовое поле пользовательской формулы. Функция принимает данные x и некоторые параметры для подгонки.
piecewiseLine( x, a, b, c, d, k )
Приложение «Фитинг кривой» создает вписывание с помощью функции.
Совет
Если требуется использовать ту же функцию для подгонки в командной строке, используйте то же выражение, что и при вводе в fittype, а затем используйте fittype в качестве входных данных для fit:
ft = fittype('piecewiseLine( x, a, b, c, d, k )');
f = fit( x, y, ft)fit функция.Чтобы подогнать пользовательские модели, выполните одно из следующих действий.
Этот пример загружает некоторые данные и использует пользовательское уравнение, определяющее модель Вейбулла, в качестве входных данных для fit функция:
time = [ 0.1; 0.1; 0.3; 0.3; 1.3; 1.7; 2.1; 2.6; 3.9; 3.9; ...
5.1; 5.6; 6.2; 6.4; 7.7; 8.1; 8.2; 8.9; 9.0; 9.5; ...
9.6; 10.2; 10.3; 10.8; 11.2; 11.2; 11.2; 11.7; 12.1; 12.3; ...
12.3; 13.1; 13.2; 13.4; 13.7; 14.0; 14.3; 15.4; 16.1; 16.1; ...
16.4; 16.4; 16.7; 16.7; 17.5; 17.6; 18.1; 18.5; 19.3; 19.7;];
conc = [0.01; 0.08; 0.13; 0.16; 0.55; 0.90; 1.11; 1.62; 1.79; 1.59; ...
1.83; 1.68; 2.09; 2.17; 2.66; 2.08; 2.26; 1.65; 1.70; 2.39; ...
2.08; 2.02; 1.65; 1.96; 1.91; 1.30; 1.62; 1.57; 1.32; 1.56; ...
1.36; 1.05; 1.29; 1.32; 1.20; 1.10; 0.88; 0.63; 0.69; 0.69; ...
0.49; 0.53; 0.42; 0.48; 0.41; 0.27; 0.36; 0.33; 0.17; 0.20;];
f = fit( time, conc, 'c*a*b*x^(b-1)*exp(-a*x^b)', 'StartPoint', [0.01, 2, 5] )
plot( f, time, conc )Определение пользовательской модели с помощью fittype, используйте форму:
f = fittype(expr)
fittype объект для выражения MATLAB, содержащегося в строке, массиве ячеек или анонимной функции expr.См. раздел fittype для получения подробной информации о:
Задание зависимых и независимых переменных, параметров задачи и коэффициентов с помощью fittype.
Задание массива элементов ячейки для использования алгоритма линейной подгонки для пользовательского уравнения. Если expr
Дополнительные сведения о линейном фитинге см. в разделе Выбор линейного фитинга в командной строке.
Примеры линейных и нелинейных пользовательских моделей.
Пошаговый пример см. в разделе Пользовательский нелинейный фитинг переписи.