Панель инструментов предоставляет одномерную и двухмерную экспоненциальную модель, как указано в
+ cedx
Экспоненты часто используются, когда скорость изменения величины пропорциональна начальной сумме величины. Если коэффициент, связанный с b и/или d, отрицательный, y представляет экспоненциальный распад. Если коэффициент положительный, y представляет экспоненциальный рост.
Например, единичная мода радиоактивного распада нуклида описывается одномерной экспоненциальной. а интерпретируется как начальное число ядер, b - константа распада, x - время, а y - число оставшихся ядер после прохождения определенного количества времени. Если существуют два режима распада, то необходимо использовать двухсрочную экспоненциальную модель. Для второго режима затухания в модель добавляется еще один экспоненциальный член.
Примеры экспоненциального роста включают заразные заболевания, для которых лекарство недоступно, и биологические популяции, рост которых не замедляется хищничеством, факторами окружающей среды и так далее.
Откройте приложение «Фитинг кривой», введя cftool. Либо щелкните Фитинг кривой (Curve Fitting) на вкладке Приложения (Apps).
В приложении «Фитинг кривой» выберите данные кривой (данные X и Y или только данные Y по индексу).
Приложение «Фитинг кривой» создает аппроксимацию кривой по умолчанию. Polynomial.
Изменение типа модели с Polynomial кому Exponential.
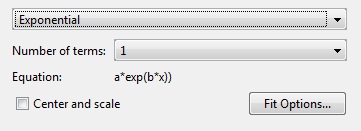
Можно задать следующие параметры:
Выберите один или два термина для соответствия exp1 или exp2.
Просмотрите на панели Результаты (Results) термины модели, значения коэффициентов и статистику соответствия.
(Необязательно) Нажмите кнопку «Параметры подгонки», чтобы задать начальные значения коэффициентов и ограничения, соответствующие данным, или измените настройки алгоритма.
Панель инструментов вычисляет оптимизированные начальные точки для экспоненциальных посадок на основе текущего набора данных. Можно переопределить начальные точки и указать собственные значения в диалоговом окне «Параметры вписывания».
Варианты подгонки для одномерной экспоненты показаны ниже. Начальные значения коэффициентов и ограничения относятся к данным переписи.
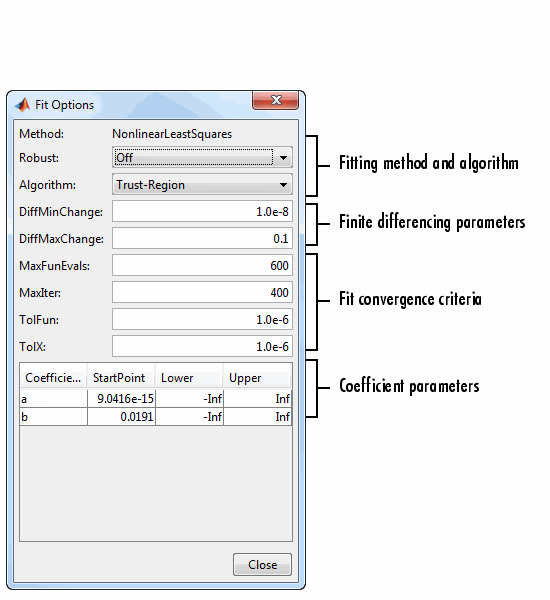
Пример задания начальных значений, соответствующих данным, см. в разделе Гауссовский фитинг с экспоненциальным фоном.
Дополнительные сведения о параметрах см. в разделах Задание параметров посадки и Оптимизированные начальные точки.
В этом примере показано, как подогнать экспоненциальную модель к данным с помощью fit функция.
Экспоненциальная библиотечная модель является входным аргументом для fit и fittype функции. Укажите тип модели 'exp1' или 'exp2' .
Соответствие одномерной экспоненциальной модели
Создавайте данные с экспоненциальным трендом, а затем подгоняйте их с помощью одномерного экспоненциального показателя. Постройте график посадки и данных.
x = (0:0.2:5)';
y = 2*exp(-0.2*x) + 0.1*randn(size(x));
f = fit(x,y,'exp1')f =
General model Exp1:
f(x) = a*exp(b*x)
Coefficients (with 95% confidence bounds):
a = 2.021 (1.89, 2.151)
b = -0.1812 (-0.2104, -0.152)
plot(f,x,y)

Подгонка двухсрочной экспоненциальной модели
f2 = fit(x,y,'exp2')f2 =
General model Exp2:
f2(x) = a*exp(b*x) + c*exp(d*x)
Coefficients (with 95% confidence bounds):
a = 2443 (-1.229e+12, 1.229e+12)
b = -0.2574 (-1.87e+04, 1.87e+04)
c = -2441 (-1.229e+12, 1.229e+12)
d = -0.2575 (-1.872e+04, 1.872e+04)
plot(f2,x,y)

Задать начальные точки
Панель инструментов вычисляет оптимизированные начальные точки для экспоненциальных посадок на основе текущего набора данных. Можно переопределить начальные точки и задать собственные значения.
Найти порядок записей для коэффициентов в первой модели ( f ) с помощью coeffnames функция.
coeffnames(f)
ans = 2x1 cell
{'a'}
{'b'}
Если указаны начальные точки, выберите значения, соответствующие данным. Задать произвольные начальные точки для коэффициентов a и b в качестве примера.
f = fit(x,y,'exp1','StartPoint',[1,2])
f =
General model Exp1:
f(x) = a*exp(b*x)
Coefficients (with 95% confidence bounds):
a = 2.021 (1.89, 2.151)
b = -0.1812 (-0.2104, -0.152)
plot(f,x,y)

Проверка параметров экспоненциального вписывания
Проверьте параметры подгонки, если требуется изменить параметры подгонки, такие как начальные значения коэффициентов и границы ограничений, соответствующие данным, или измените настройки алгоритма. Дополнительные сведения об этих опциях см. в таблице свойств для нелинейных квадратов fitoptions справочная страница.
fitoptions('exp1')ans =
Normalize: 'off'
Exclude: []
Weights: []
Method: 'NonlinearLeastSquares'
Robust: 'Off'
StartPoint: [1x0 double]
Lower: [1x0 double]
Upper: [1x0 double]
Algorithm: 'Trust-Region'
DiffMinChange: 1.0000e-08
DiffMaxChange: 0.1000
Display: 'Notify'
MaxFunEvals: 600
MaxIter: 400
TolFun: 1.0000e-06
TolX: 1.0000e-06
fit | fitoptions | fittype