Следующие темы соответствуют некоторым данным переписи с использованием полиномиальных уравнений вплоть до шестой степени и одномерного экспоненциального уравнения. Шаги демонстрируют, как:
Загрузка данных и изучение различных вариантов подгонки с использованием различных библиотечных моделей.
Поиск наилучшего вписывания по:
Сравнение результатов графического подбора
Сравнение результатов численного соответствия, включая соответствующие коэффициенты и статистику соответствия
Экспортируйте результаты наилучшего вписывания в рабочую область MATLAB ® для анализа модели в командной строке.
Сохраните сеанс и создайте код MATLAB для всех посадок и графиков.
Перед подгонкой данных с помощью приложения «Фитинг кривой» необходимо загрузить переменные данных в рабочее пространство MATLAB. В этом примере данные хранятся в файле MATLAB. census.mat.
Загрузите данные:
load census
Рабочая область содержит две новые переменные:
cdate - вектор столбца, содержащий годы, 1790 для 1990 с приращением на 10 лет.
pop - вектор столбца с цифрами населения США, которые соответствуют годам в cdate.
Откройте приложение «Фитинг кривой»:
cftool
Выберите имена переменных cdate и pop из списков данных X и Y.
Приложение «Фитинг кривой» создает и строит график посадки по умолчанию для входных данных X (или данных предиктора) и выходных данных Y (или данных ответа). Аппроксимация по умолчанию является типом линейной полиномиальной аппроксимации. Наблюдение за отображением параметров посадки Polynomial, степени 1.
Изменение аппроксимации на полином второй степени путем выбора 2 из списка «Степень».
Приложение «Фитинг кривой» отображает новое вписывание. Приложение «Фитинг кривой» вычисляет новое вписывание при изменении параметров вписывания, поскольку по умолчанию выбран параметр «Автоматическое вписывание». Если переопределение занимает много времени, например, для больших наборов данных, можно отключить функцию автоматического вписывания путем снятия флажка.
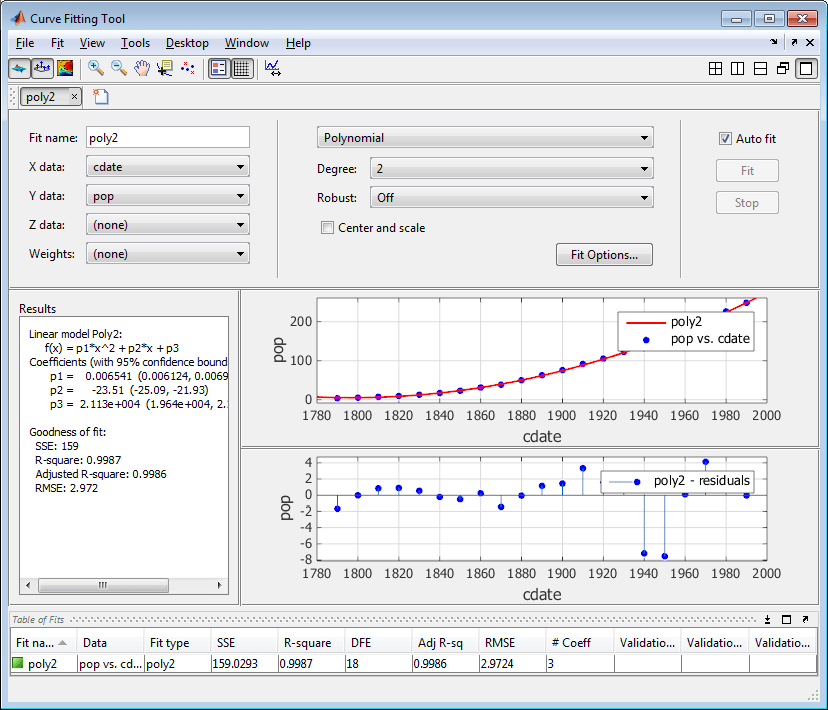
Приложение «Подбор кривой» отображает результаты подбора данных переписи с помощью квадратичного полинома на панели «Результаты», где можно просмотреть библиотечную модель, подогнанные коэффициенты и статистику соответствия.
Изменение имени вписывания на poly2.
Просмотрите остатки, выбрав меню «Вид» > «Остатки» «Печать».
Остатки указывают на то, что возможно лучшее вписывание. Поэтому продолжайте изучать различные варианты набора данных переписи.
Добавьте новые посадки, чтобы попробовать другие уравнения библиотеки.
Щелкните правой кнопкой мыши посадку в таблице посадок и выберите "Копировать" "poly2"(или используйте меню" Вписать ").
Совет
Для посадок данного типа (например, многочленов) используйте команду "Копировать" "fitname"вместо новой посадки, поскольку копирование посадки требует меньшего количества шагов. Дублированная аппроксимация содержит те же параметры выбора данных и настройки аппроксимации.
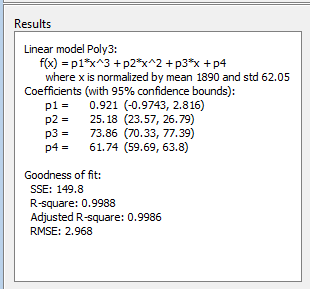
Изменение степени полинома на 3 и переименуйте посадку poly3.
При подгонке полиномов более высокой степени на панели Результаты (Results) отображается следующее предупреждение:
Equation is badly conditioned. Remove repeated data points or try centering and scaling.
Нормализуйте данные, установив флажок Центр и масштаб (Center and scale).
Повторите шаги a и b, чтобы добавить аппроксимацию полинома до шестой степени, а затем добавьте экспоненциальную аппроксимацию.
Для каждого нового вписывания просмотрите информацию о панели «Результаты» (Results) и график остатков в приложении «Фитинг кривой» (Curve Fitting).
Остатки от хорошей посадки должны выглядеть случайными без видимого рисунка. Шаблон, такой как тенденция к тому, чтобы последовательные остатки имели один и тот же знак, может быть показателем того, что существует лучшая модель.
Предупреждение о масштабировании возникает, поскольку процедура фитинга использует cdate значения в качестве основы для матрицы с очень большими значениями. Распространение cdate значения приводят к проблеме масштабирования. Для решения этой проблемы можно нормализовать cdate данные. Нормализация масштабирует данные предиктора для повышения точности последующих числовых вычислений. Способ нормализации cdate - центрировать его при нулевом среднем значении и масштабировать до стандартного отклонения единицы. Эквивалентный код:
(cdate - mean(cdate))./std(cdate)
Примечание
Поскольку данные предиктора изменяются после нормализации, значения соответствующих коэффициентов также изменяются по сравнению с исходными данными. Однако функциональная форма данных и результирующая статистика соответствия не изменяются. Кроме того, данные отображаются на графиках приложения «Фитинг кривой» с использованием исходного масштаба.
Для определения наилучшего вписывания необходимо изучить как графические, так и числовые результаты вписывания.
Определите наилучшее соответствие, изучив графики посадок и остатков. Чтобы просмотреть графики для каждого вписывания по очереди, дважды щелкните вписывание в таблице посадок. Результаты графического подбора показывают, что:
Посадки и остатки для полиномиальных уравнений все похожи, что затрудняет выбор лучшего.
Аппроксимация и остатки для одномерного экспоненциального уравнения указывают на плохую аппроксимацию в целом. Поэтому это плохой выбор, и вы можете удалить экспоненциальную посадку из кандидатов на лучшую посадку.
Изучите поведение приспособлений вплоть до 2050 года. Цель подбора данных переписи состоит в том, чтобы экстраполировать наиболее подходящие для прогнозирования будущих значений численности населения.
Дважды щелкните полиномиальную подгонку шестой степени в таблице посадок, чтобы просмотреть графики для этой подгонки.
Измените границы осей графиков, выбрав меню «Инструменты» > «Границы осей».
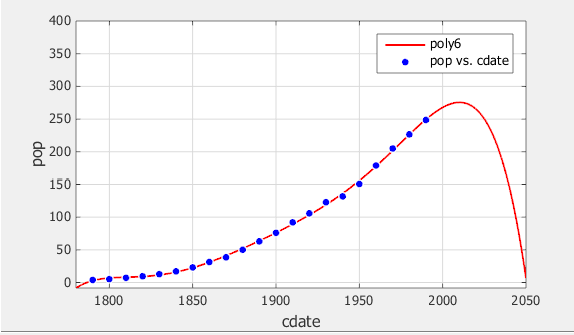
Изменение максимума X (cdate) на 2050и увеличьте значение Main Y (pop) Maximum до 400и нажмите Enter.
Проверьте график посадки. Поведение подгонки полинома шестой степени за пределы диапазона данных делает его плохим выбором для экстраполяции, и вы можете отклонить эту подгонку.
Если вы больше не можете устранить посадки, рассматривая их графически, вам следует изучить результаты численного соответствия. Приложение «Фитинг кривой» отображает два типа результатов численного вписывания:
Статистика пригодности
Доверительные границы по установленным коэффициентам
Статистика соответствия помогает определить, насколько хорошо кривая соответствует данным. Доверительные границы коэффициентов определяют их точность.
Проверьте результаты численного соответствия:
Для каждого вписывания просмотрите статистику соответствия на панели Результаты (Results).
Сравните все посадки одновременно в таблице посадок. Щелкните заголовки столбцов для сортировки по результатам статистики.
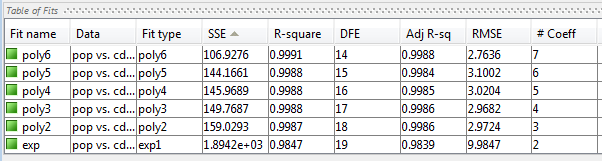
Проверьте сумму квадратов из-за ошибки (SSE) и скорректированную статистику R-квадратов, чтобы помочь определить наилучшее соответствие. Статистика SSE представляет собой ошибку наименьших квадратов аппроксимации, причем значение ближе к нулю указывает на лучшую аппроксимацию. Скорректированная статистика R-квадрата, как правило, является лучшим показателем качества посадки при добавлении дополнительных коэффициентов к модели.
Крупнейшая МРЗ для exp1 указывает на плохую подгонку, которую вы уже определили, проверяя подгонку и остатки. Наименьшее значение SSE связано с poly6. Однако поведение этого вписывания за пределы диапазона данных делает его плохим выбором для экстраполяции, поэтому вы уже отклонили это вписывание, изучив графики с новыми пределами оси.
Следующее наилучшее значение SSE связано с аппроксимацией полинома пятой степени, poly5, предполагая, что это может быть наилучшим образом подходит. Однако SSE и скорректированные значения R-квадрата для остальных полиномиальных посадок очень близки друг к другу. Какой выбрать?
Решите проблему наилучшего вписывания, проверив доверительные границы для остальных посадок на панели Результаты (Results). Дважды щелкните аппроксимацию в таблице посадок, чтобы открыть (или сфокусировать, если она уже открыта) фигуру аппроксимации и просмотреть панель Результаты (Results). Фигура посадки отображает настройки посадки, панель результатов и графики для одной посадки.
Отображение многочлена пятой степени и poly2 подгонять фигуры бок о бок. Изучение результатов бок о бок может помочь вам оценить соответствия.
Для одновременного отображения двух фигур подгонки используйте элементы управления разметкой в правом верхнем углу приложения «Фитинг кривой» или выберите «Окно» > «Левая/Правая плитка» или «Верхняя/Нижняя плитка».
Чтобы изменить отображаемые посадки, щелкните, чтобы выбрать фигуру посадки, а затем дважды щелкните по посадке, которая должна отображаться в таблице посадок.
Сравните коэффициенты и границы (p1, p2и так далее) на панели «Результаты» для обоих посадок, poly5 и poly2. Панель инструментов вычисляет 95% доверительные границы коэффициентов. Доверительные границы коэффициентов определяют их точность. Проверьте уравнения на панели «Результаты» (f(x)=p1*x+p2*x...), чтобы увидеть модельные термины для каждого коэффициента. Обратите внимание, что p2 относится к p2*x срок в Poly2 и p2*x^4 срок в Poly5. Не сравнивайте нормализованные коэффициенты непосредственно с ненормализованными коэффициентами.
Совет
Используйте меню Вид (View), чтобы скрыть Настройки вписывания (Fit Settings) или Таблица посадок (Table of Fits), если требуется больше места для просмотра и сравнения графиков и результатов, как показано ниже. Можно также скрыть панель Результаты (Results), чтобы показать только графики.
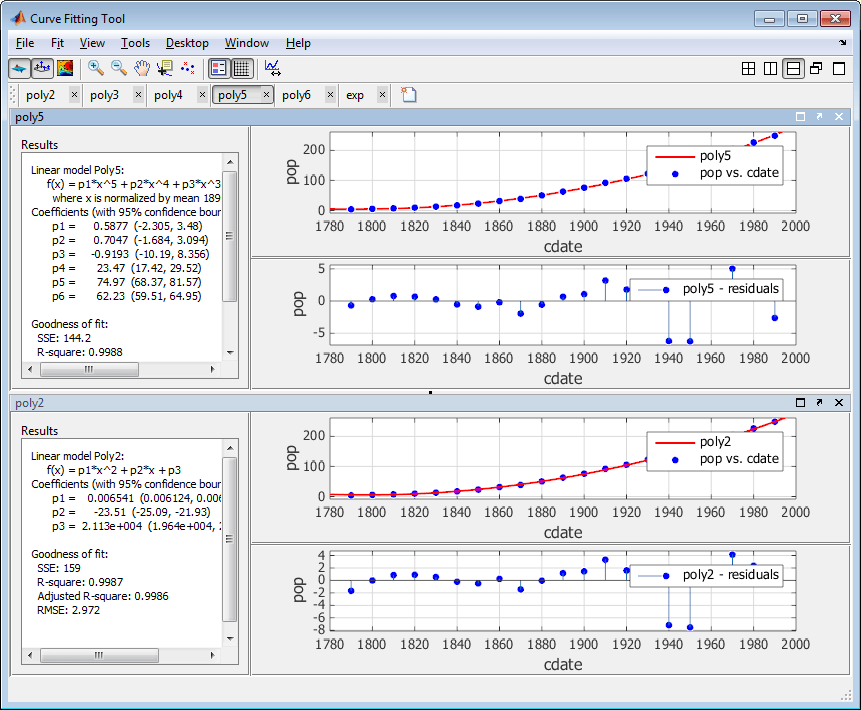
Границы пересекают ноль на p1, p2, и p3 коэффициенты для многочлена пятой степени. Это означает, что вы не можете быть уверены, что эти коэффициенты отличаются от нуля. Если модельные термины более высокого порядка могут иметь нулевые коэффициенты, то они не помогают при подгонке, что позволяет предположить, что эта модель переопределяет данные переписи.
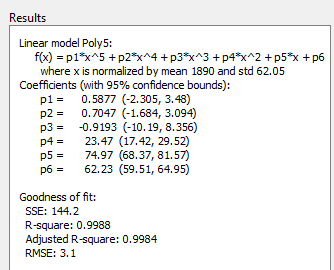
Однако малые доверительные границы не пересекают ноль на p1, p2, и p3 для квадратичной посадки, poly2 указывают, что соответствующие коэффициенты известны достаточно точно.

Поэтому, изучив как графические, так и числовые результаты подгонки, необходимо выбрать poly2 как наилучшее решение для экстраполяции данных переписи.
Примечание
Соответствующие коэффициенты, связанные с постоянным, линейным и квадратичным членами, почти идентичны для каждого нормализованного полиномиального уравнения. Однако по мере увеличения степени полинома границы коэффициентов, связанные с членами более высокой степени, пересекают ноль, что предполагает переоснащение.
Можно использовать команду Сохранить в рабочую область (Save to Workspace) для экспорта выбранного вписывания и связанных результатов вписывания в рабочую область MATLAB. Аппроксимация сохраняется как объект MATLAB, а связанные результаты аппроксимации сохраняются как структуры.
Щелкните правой кнопкой мыши poly2 Поместитесь в таблице посадок и выберите Сохранить «poly2» в рабочей области (или используйте меню Посадка).
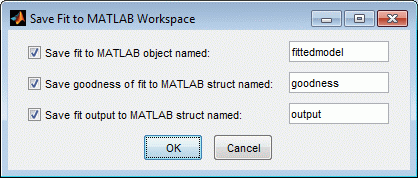
Нажмите кнопку ОК, чтобы сохранить имена по умолчанию.
fittedmodel сохраняется как фитинг кривой Toolbox™ cfit объект.
>> whos fittedmodel Name Size Bytes Class fittedmodel 1x1 822 cfit
Осмотрите fittedmodel cfit объект для отображения модели, подгоняемых коэффициентов и доверительных границ для подгоняемых коэффициентов:
fittedmodel
fittedmodel =
Linear model Poly2:
fittedmodel(x) = p1*x^2 + p2*x + p3
Coefficients (with 95% confidence bounds):
p1 = 0.006541 (0.006124, 0.006958)
p2 = -23.51 (-25.09, -21.93)
p3 = 2.113e+004 (1.964e+004, 2.262e+004)Осмотрите goodness структура для отображения результатов соответствия:
goodness
goodness =
sse: 159.0293
rsquare: 0.9987
dfe: 18
adjrsquare: 0.9986
rmse: 2.9724Осмотрите output структура для отображения дополнительной информации, связанной с посадкой, такой как остатки:
output
output =
numobs: 21
numparam: 3
residuals: [21x1 double]
Jacobian: [21x3 double]
exitflag: 1
algorithm: 'QR factorization and solve'
iterations: 1С помощью различных функций постобработки можно вычислять (интерполировать или экстраполировать), дифференцировать или интегрировать аппроксимацию по определенному диапазону данных.
Например, чтобы вычислить fittedmodel при векторе значений для экстраполяции к 2050 году введите:
y = fittedmodel(2000:10:2050) y = 274.6221 301.8240 330.3341 360.1524 391.2790 423.7137
plot(fittedmodel, cdate, pop) hold on plot(fittedmodel, 2000:10:2050, y) hold off
Пример воспроизведения этого интерактивного анализа данных переписи с помощью командной строки см. в разделе Подгонка полиномиальной кривой.
Панель инструментов предоставляет несколько вариантов сохранения работы. Можно сохранить одно или несколько посадок и связанные с ними результаты посадки в качестве переменных в рабочей области MATLAB. Затем эту сохраненную информацию можно использовать для создания документации или для расширения процесса исследования и анализа данных. Помимо сохранения работы в переменных рабочей области MATLAB, можно выполнить следующие действия.
Сохраните текущий сеанс фитинга кривой, выбрав команду Файл (File) > Сохранить сеанс (Save Session). Файл сеанса содержит все посадки и переменные в сеансе и запоминает макет. См. раздел Сохранение и перезагрузка сеансов.
Создайте код MATLAB для повторного создания всех посадок и графиков в сессии, выбрав команду «Файл» > «Создать код». Приложение «Фитинг кривой» генерирует код из сессии и отображает файл в редакторе MATLAB.
Можно воссоздать посадки и графики, вызвав файл в командной строке с исходными данными в качестве входных аргументов. Можно также вызвать файл с новыми данными и автоматизировать процесс подбора нескольких наборов данных. Дополнительные сведения см. в разделе Создание кода из приложения «Фитинг кривой».