Коэффициенты Тейлора
taylor = fntlr(f,dorder,x)
taylor = fntlr(f,dorder,x) возвращает ненормализованные коэффициенты Тейлора вплоть до заданного порядка dorder и на данном x, функции, описанной в f .
Для одномерной функции и скаляра x, это вектор
Ddorder − 1f (x)]
Если, в более общем смысле, функция в f является d-значение с d>1 или даже prod(d)>1 и/или является m-вариат для некоторых m>1, то dorder ожидается, что это будет m-вектор положительных целых чисел, x ожидается, что это будет матрица с m строки, и, в этом случае, выход имеет размер [prod(d)*prod(dorder),size(x,2)], с его j-й колонкой, содержащей
Dmim − 1f (x (:, j))
для i1=1:dorder(1), ..., im=1:dorder(m). Здесь Dif - частная производная f относительно его i-го аргумента.
Если f содержит одномерную функцию и x является скалярной или 1-строчной матрицей, то fntlr(f,3,x) создает те же выходные данные, что и операторы
df = fnder(f); [fnval(f,x); fnval(df,x); fnval(fnder(df),x)];
В качестве более сложного примера рассмотрим векторы Тейлора порядка 3 в 21 равноотстоящей точке для рационального сплайна, граф которого является единичной окружностью:
ci = rsmak('circle'); in = fnbrk(ci,'interv');
t = linspace(in(1),in(2),21); t(end)=[];
v = fntlr(ci,3,t);
Строим заговор ci вместе с точками v(1:2,:), чтобы убедиться, что это действительно точки на единичной окружности.
fnplt(ci), hold on, plot(v(1,:),v(2,:),'o')
Далее, чтобы проверить, что v(3:4,j) - вектор, касательный к окружности в точке, v(1:2,j), мы используем MATLAB
®quiver для добавления соответствующих стрелок к нашему графику:
quiver(v(1,:),v(2,:),v(3,:),v(4,:))
Наконец, как насчет v(5:6,:)? Это вторые производные, и мы добавляем соответствующие стрелки следующим образом quiver , заканчивая первую и вторую производные рационального сплайна, дающего круг.
quiver(v(1,:),v(2,:),v(5,:),v(6,:)), axis equal, hold off
Первая и вторая производные рационального сплайна, дающие круг
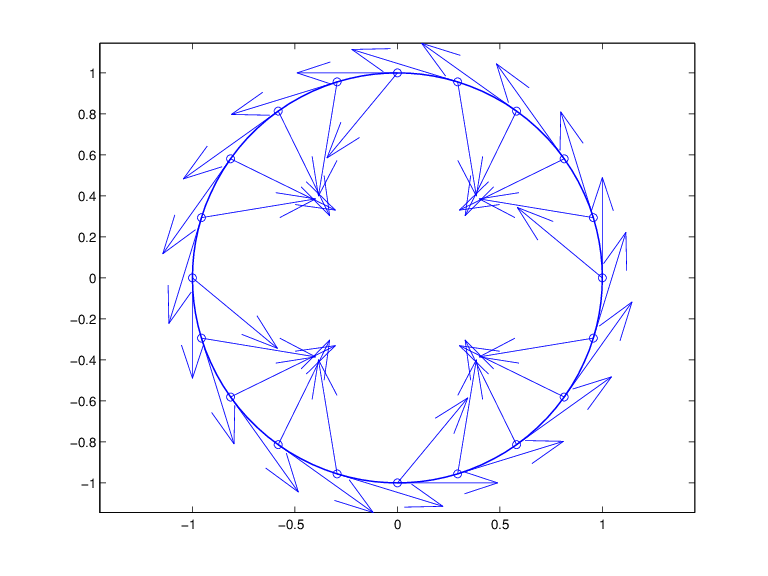
Теперь, наша кривая - окружность, вы могли ожидать, что стрелки 2-й производной будут указывать прямо к центру этой окружности, и это было бы действительно так, если бы функция в ci использовал длину дуги в качестве своей независимой переменной. Поскольку используемый параметр не является длиной дуги, мы используем формулу, приведенную в примере: B-форма сплайновое приближение к окружности, чтобы вычислить кривизну кривой, заданную ci в этих выбранных точках. Для удобства сравнения мы переключаемся на переменные, используемые там, а затем просто используем команды оттуда.
dspt = v(3:4,:); ddspt = v(5:6,:); kappa = abs(dspt(1,:).*ddspt(2,:)-dspt(2,:).*ddspt(1,:))./... (sum(dspt.^2)).^(3/2); max(abs(kappa-1)) ans = 2.2204e-016
Численный ответ успокаивает: во всех проверенных точках кривизна составляет от 1 до в пределах скругления.