Панель инструментов предоставляет (полиномиальные) функции сплайна в любом числе переменных, как тензорные произведения одномерных сплайнов. Эти многомерные сплайны имеют обе стандартные формы: B-форму и ppform, а их конструкция и использование являются параллелями одномерных сплайнов, описанных в предыдущих разделах «Конструирование и работа со сплайнами ppform» и «Конструирование и работа со сплайнами B-формы». Для их построения и использования используются одни и те же команды.
Для простоты следующее обсуждение касается только двумерных сплайнов.
Тензор-продукт идея очень проста. Если f является функцией x, а g является функцией y, то их тензор-произведение p (x, y): = f (x) g (y) является функцией x и y, то есть двумерной функцией. В более общем случае с s = (s1,..., sm + h) и t = (t1,..., tn + k) узловыми последовательностями и aij (i = 1,..., m; j = 1,... n) соответствующий массив коэффициентов, получается двумерный сплайн как
, tj + k) aij
B-форма этого сплайна содержит массив ячеек {s, t} его узловых последовательностей, массив коэффициентов a, вектор чисел [m, n] и вектор порядков [h, k]. Команда
sp = spmak({s,t},a);
конструирует эту форму. Далее, fnplt, fnval, fnder, fndir, fnrfn, и fn2fm может использоваться для печати, оценки, дифференциации и интеграции, уточнения и преобразования этой формы.
Наиболее вероятно, что вы создадите такую форму путем поиска интерполятора или аппроксиманта к данным с привязкой к сетке. Например, если известны значения z (i, j) = g (x (i), y (j)), i = 1: m, j = 1: n, некоторой функции g во всех точках прямоугольной сетки, то, если предположить, что строго возрастающая последовательностьx удовлетворяет условиям Шёнберга-Уитни по отношению к вышеуказанной последовательности s узлов, и что строго возрастающая последовательность y удовлетворяет условиям Шёнберга-Уитни в отношении вышеуказанной последовательности узлов t, команда
sp=spapi({s,t},[h,k],{x,y},z);создает уникальный двумерный сплайн вышеуказанной формы, соответствующий заданным значениям. Команда fnplt(sp) дает быстрый график этого интерполятора. Команда pp = fn2fm(sp,'pp') дает pppform этого сплайна, что, вероятно, то, что вы хотите, когда вы хотите оценить сплайн в тонкой сетке ((xx(i),yy(j)) для i=1:M, j=1:N), по команде:
values = fnval(pp,{xx,yy});
Ppform такого двумерного сплайна содержит, аналогично, клеточный массив последовательностей разрыва, многомерный массив коэффициентов, вектор числовых частей и вектор полиномиальных порядков. К счастью, панель инструментов настроена таким образом, что обычно нет причин беспокоиться об этих деталях любой из форм. Интерполяция, аппроксимация или сглаживание используются для построения сплайнов, а затем используются fn... команды для их использования.
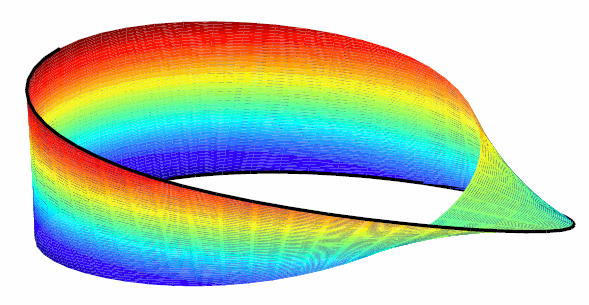
Вот пример поверхности, построенной как двумерный сплайн с 3D знаком. Поверхность - знаменитая полоса Мёбиуса, получаемая взятием длинной полоски бумаги и склеиванием её узких концов вместе, но с перекручиванием. Рисунок получается по следующим командам:
x = 0:1; y = 0:4; h = 1/4; o2 = 1/sqrt(2); s = 2; ss = 4;
v(3,:,:) = h*[0, -1, -o2, 0, o2, 1, 0;0, 1, o2, 0, -o2, -1, 0];
v(2,:,:) = [ss, 0, s-h*o2, 0, -s-h*o2, 0, ss;...
ss, 0, s+h*o2, 0,-s+h*o2, 0, ss];
v(1,:,:) = s*[0, 1, 0, -1+h, 0, 1, 0; 0, 1, 0, -1-h, 0, 1, 0];
cs = csape({x,y},v,{'variational','clamped'});
fnplt(cs), axis([-2 2 -2.5 2.5 -.5 .5]), shading interp
axis off, hold on
values = squeeze(fnval(cs,{1,linspace(y(1),y(end),51)}));
plot3(values(1,:), values(2,:), values(3,:),'k','linew',2)
view(-149,28), hold off
Полоса Мёбиуса, выполненная векторной двухмерной интерполяцией сплайна