Рациональные модели определяются как отношения многочленов и задаются
где n - степень многочлена числителя и 0 ≤ n ≤ 5, в то время как m - степень многочлена знаменателя и 1 ≤ m ≤ 5. Следует отметить, что коэффициент, связанный с xm, всегда равен 1. Это делает числитель и знаменатель уникальными, когда степени многочлена одинаковы.
В этом руководстве обоснование описывается в терминах степени числителя/степени знаменателя. Например, квадратичное/кубическое рациональное уравнение задается как
q1x2 + q2x + q3
Как и многочлены, рациональные часто используются, когда требуется простая эмпирическая модель. Основным преимуществом рациональных решений является их гибкость с данными, которые имеют сложную структуру. Главный недостаток заключается в том, что они становятся нестабильными, когда знаменатель находится около 0. Пример использования рациональных многочленов различных степеней см. в разделе Пример: Рациональное вписывание.
Откройте приложение «Фитинг кривой», введя cftool. Либо щелкните Фитинг кривой (Curve Fitting) на вкладке Приложения (Apps).
В приложении «Фитинг кривой» выберите данные кривой (данные X и Y или только данные Y по индексу).
Приложение «Фитинг кривой» создает аппроксимацию кривой по умолчанию. Polynomial.
Изменение типа модели с Polynomial кому Rational.
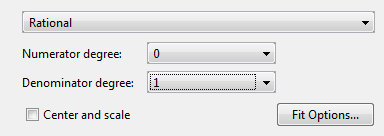
Можно задать следующие параметры:
Выберите степень многочлена числителя и знаменателя. Числитель может иметь степень 0 кому 5, и знаменатель из 1 кому 5.
Просмотрите на панели Результаты (Results) термины модели, значения коэффициентов и статистику соответствия.
(Необязательно) Нажмите кнопку «Параметры подгонки», чтобы задать начальные значения коэффициентов и ограничения или изменить настройки алгоритма.
Панель инструментов вычисляет случайные начальные точки для рациональных моделей, определенных на интервале [0,1]. Можно переопределить начальные точки и указать собственные значения в диалоговом окне «Параметры вписывания».
Дополнительные сведения о параметрах см. в разделах Задание параметров посадки и Оптимизированные начальные точки.
Укажите тип модели ratijгде i - степень многочлена числителя, а j - степень многочлена знаменателя. Например, 'rat02', 'rat21' или 'rat55'.
Например, чтобы загрузить некоторые данные и подогнать рациональную модель:
load hahn1; f = fit( temp, thermex, 'rat32') plot(f,temp,thermex)
См. Пример: Рациональная посадка, чтобы совместить этот пример в интерактивном режиме с различными рациональными моделями.
Если требуется изменить параметры подгонки, такие как начальные значения коэффициентов и границы ограничений, соответствующие данным, или изменить настройки алгоритма, см. таблицу дополнительных свойств с NonlinearLeastSquares на fitoptions справочная страница.
Этот пример подгоняет измеренные данные с использованием рациональной модели. Данные описывают коэффициент теплового расширения для меди как функцию температуры в градусах кельвина.
Для этого набора данных вы найдете рациональное уравнение, которое обеспечивает наилучшее соответствие. Рациональные модели определяются как отношение многочленов, задаваемое:
q1xm − 1 +... + qm
где n - степень многочлена числителя, а m - степень многочлена знаменателя. Следует отметить, что рациональные уравнения не связаны с физическими параметрами данных. Вместо этого они обеспечивают простую и гибкую эмпирическую модель, которую можно использовать для интерполяции и экстраполяции.
Загрузка данных теплового расширения из файла hahn1.mat, которая снабжена панелью инструментов.
load hahn1
Рабочая область содержит две новые переменные:
temp - вектор температур в градусах кельвина.
thermex - вектор коэффициентов теплового расширения для меди.
Откройте приложение «Фитинг кривой», введя:
cftool
Выбрать temp и thermex из списков данных X и Y.
Приложение «Фитинг кривой» подходит и отображает данные.
Выбрать Rational в списке подходящих категорий.
Попробуйте первый выбор для рациональной модели квадратичной/квадратичной. Выбрать 2 как для степени числителя, так и для степени знаменателя.
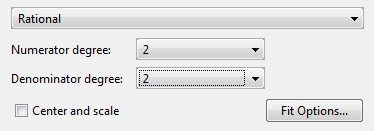
Приложение «Аппроксимация кривой» соответствует квадратичному/квадратичному рациональному.
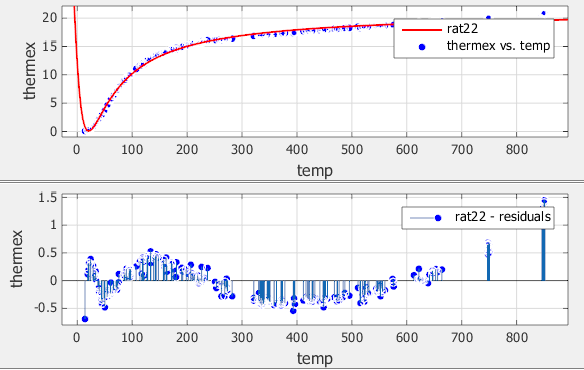
Проверьте остатки. Выберите меню «Вид» > «Остатки» «Печать» или нажмите кнопку на панели инструментов.
Проверьте данные, подгонку и остатки. Обратите внимание, что при подгонке пропускаются данные для наименьших и наибольших предикторных значений. Кроме того, остатки показывают сильный шаблон во всем наборе данных, что указывает на возможность лучшего соответствия.
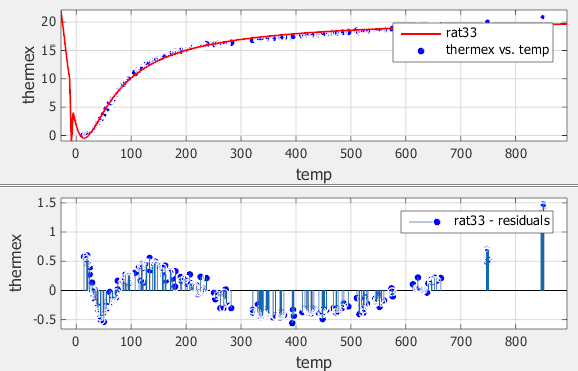
Для следующей посадки попробуйте кубическое/кубическое уравнение. Выбрать 3 как для степени числителя, так и для степени знаменателя.
Проверьте данные, подгонку и остатки. Посадка имеет несколько разрывов вокруг нулей знаменателя.
Примечание
Результаты зависят от случайных начальных точек и могут отличаться от показанных.
Просмотрите область «Результаты». Сообщение и числовые результаты показывают, что посадка не сошлась.
Fit computation did not converge: Fitting stopped because the number of iterations or function evaluations exceeded the specified maximum.
Несмотря на то, что сообщение на панели Результаты (Results) показывает, что при увеличении максимального числа итераций можно улучшить аппроксимацию, на данном этапе процесса аппроксимации лучше использовать другое рациональное уравнение, поскольку текущая аппроксимация содержит несколько разрывов. Эти разрывы обусловлены тем, что функция раздувается при предикторных значениях, которые соответствуют нулям знаменателя.
Попробуйте подогнать данные с помощью кубического/квадратичного уравнения. Выбрать 2 для степени знаменателя и оставьте для степени числителя значение 3.
Входные переменные имеют очень разные масштабы, поэтому выберите опцию «Центр и масштаб».
Данные, аппроксимация и остатки показаны ниже.
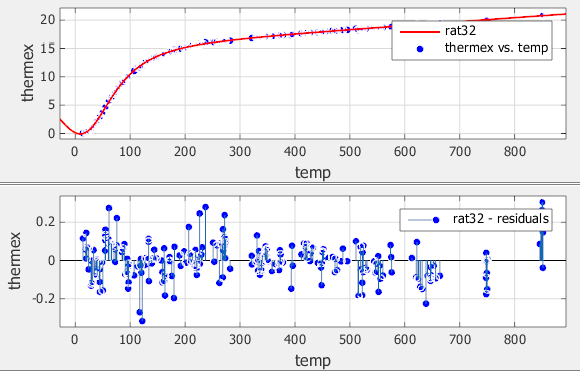
Посадка хорошо себя ведет по всему диапазону данных, и остатки случайным образом рассеиваются около нуля. Поэтому можно уверенно использовать эту подгонку для дальнейшего анализа.
fit | fitoptions | fittype