Если данные зашумлены, их можно подогнать с помощью сглаживающего сплайна. Можно также использовать один из методов сглаживания, описанных в разделе Фильтрация и сглаживание данных.
Сглаживающий сплайн s строится для указанного параметра сглаживания p и указанных весов wi. Сглаживающий сплайн сводит к минимуму
(d2sdx2) 2dx
Если веса не указаны, предполагается, что они равны 1 для всех точек данных.
p определяется между 0 и 1. p = 0 создает прямолинейную подгонку наименьших квадратов к данным, в то время как p = 1 создает кубический сплайн-интерполятор. Если параметр сглаживания не указан, он автоматически выбирается в «интересном диапазоне». Интересный диапазон p часто близок к 1/( 1 + h3/6), где h - среднее расстояние между точками данных, и обычно он намного меньше допустимого диапазона параметра. Поскольку сглаживающие сплайны имеют связанный параметр сглаживания, в этом смысле эти посадки можно считать параметрическими. Однако сглаживающие сплайны также являются кусочными многочленами, такими как кубический сплайн или разделители, сохраняющие форму, и считаются непараметрическим типом посадки в этой направляющей.
Примечание
Алгоритм сглаживания сплайна основан на csaps функция.
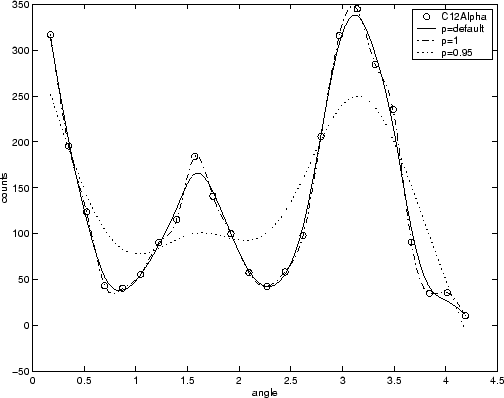
Данные ядерной реакции из файла carbon12alpha.mat показаны здесь с тремя сглаживающими сплайновыми посадками. Параметр сглаживания по умолчанию (p = 0,99) создает самую гладкую кривую. Кубическая сплайновая кривая (p = 1) проходит через все точки данных, но не такая гладкая. Третья кривая (p = 0,95) пропускает данные с большим отрывом и иллюстрирует, насколько малым может быть «интересный диапазон» p.
В приложении «Фитинг кривой» выберите Smoothing Spline из списка типов модели.
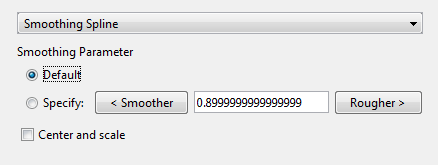
Можно задать следующие параметры:
Чтобы сделать более гладкую подгонку дальше от данных, нажимайте кнопку < Smoother до тех пор, пока график не покажет нужную плавность.
Чтобы сделать более грубую посадку ближе к данным, нажмите кнопку «Грубая >» до тех пор, пока график не будет удовлетворен.
Можно также задать любое значение параметра сглаживания от 0 до 1. 0 создает линейную полиномиальную аппроксимацию (аппроксимацию данных методом наименьших квадратов), в то время как 1 создает кусочно-кубическую полиномиальную аппроксимацию, которая проходит через все точки данных (кубический сплайн-интерполятор).
Щелкните По умолчанию (Default), чтобы вернуться к начальному значению. Панель инструментов пытается выбрать значение по умолчанию, соответствующее данным. См. раздел Сведения о сглаживании сплайнов.
Например:
Загрузите данные в окне «О сглаживании сплайнов», введя:
load carbon12alpha
В приложении «Фитинг кривой» выберите angle для данных X и counts для данных Y.
Выберите Smoothing Spline тип посадки.
Попробуйте сглаживать значения параметров 1, 0.95и значение по умолчанию (0,99).
fit ФункцияВ этом примере показано, как использовать fit для подгонки сглаживающей сплайновой модели к данным.
Подгонка сглаживающей сплайновой модели
Загрузка данных и подгонка сглаживающей сплайновой модели путем задания 'smoothingspline' при вызове функции посадки.
load enso f = fit(month,pressure,'smoothingspline'); plot(f,month,pressure)

Просмотр вычисленного параметра сглаживания
Создайте модель еще раз и используйте третий выходной аргумент для просмотра вычисленного параметра сглаживания. Параметр сглаживания - p значение в поле out структура. Значение по умолчанию зависит от набора данных.
[f,gof,out] = fit(month,pressure,'smoothingspline');
out.pans = 0.9000
Задать параметр сглаживания с помощью 'SmoothingParam'
Задайте параметр сглаживания для нового вписывания с помощью 'SmoothingParam' вариант. Его значение должно быть в диапазоне от 0 до 1.
f = fit(month,pressure,'smoothingspline','SmoothingParam',0.07); plot(f,month,pressure)

Задать параметр сглаживания с помощью fitoptions
В качестве альтернативы можно использовать fitoptions для задания параметра сглаживания перед подгонкой.
options = fitoptions('Method','Smooth','SmoothingParam',0.07); [f,gof,out] = fit(month,pressure,'smooth',options); out.p
ans = 0.0700
Для альтернативы 'smoothingspline', можно использовать функцию кубического сглаживания csaps или другие функции сплайна, которые обеспечивают больший контроль над тем, что можно создать. См. раздел Сведения о сплайнах в панели инструментов фитинга кривой.
В этом примере некоторые данные подгоняются с использованием интерполятора кубического сплайна и нескольких сглаживающих сплайнов.
Создайте переменные в рабочей области:
x = (4*pi)*[0 1 rand(1,25)]; y = sin(x) + .2*(rand(size(x))-.5);
Откройте приложение «Фитинг кривой», введя:
cftool
Выбрать x и y из списков данных X и Y.
Приложение «Фитинг кривой» подходит и отображает данные.
Подгонка данных с помощью интерполятора кубического сплайна путем выбора типа подгонки Interpolant и метода Cubic.
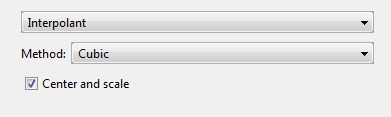
Приложение «Фитинг кривой» подходит и отображает интерполятор кубического сплайна.
Введите имя посадки cubicsp.
Просмотр панели «Результаты». Статистика пригодности, такая как RMSE, не определена (показана как NaN) для интерполяторов.
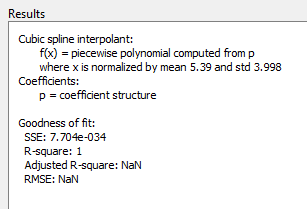
Интерполяция кубического сплайна определяется как кусочный многочлен, который приводит к структуре коэффициентов (p). Число «частей» в структуре на единицу меньше, чем количество подогнанных точек данных, а число коэффициентов для каждой части равно четырем, поскольку степень полинома равна трем. Можно изучить структуру коэффициентов. p при экспорте в рабочее пространство (например, введите fitname.p
Создайте другое вписывание для сравнения. Щелкните правой кнопкой мыши в таблице посадок и выберите Дублировать «cubicsp».
Поместите данные в сглаживающий сплайн, выбрав «Сглаживание сплайна».
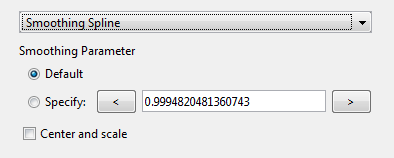
Уровень сглаживания задается параметром сглаживания. Значение параметра сглаживания по умолчанию зависит от набора данных и автоматически вычисляется панелью инструментов.
Для этого набора данных параметр сглаживания по умолчанию близок к 1, что указывает на то, что сглаживающий сплайн почти кубический и очень близок к проходу через каждую точку данных.
Присвойте имя подгонке параметра сглаживания по умолчанию Smooth1. Если уровень сглаживания, создаваемый параметром сглаживания по умолчанию, не нравится, можно указать любое значение от 0 до 1. 0 создает линейную полиномиальную аппроксимацию, в то время как 1 создает кусочно-кубическую полиномиальную аппроксимацию, которая проходит через все точки данных.
Здесь показаны числовые результаты сглаживания сплайновой посадки.
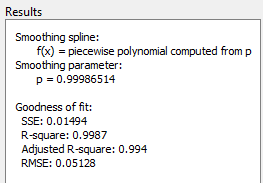
Для сравнения создайте другой сглаживающий сплайн. Щелкните правой кнопкой мыши в таблице посадок и выберите пункт «Дублировать» (Duplicate) 1. Измените параметр сглаживания на 0.5 и присвойте имя посадке Smooth2.
Сравните графики для ваших трех посадок. Изучите поведение посадки за пределами данных, увеличив масштаб абсцисс по умолчанию. Границы осей можно изменить с помощью меню «Сервис» > «Управление пределом осей».
Примечание
Результаты зависят от случайных начальных точек и могут отличаться от описанных.
Обратите внимание, что параметр сглаживания по умолчанию создает кривую, которая является более гладкой, чем интерполятор, но хорошо вписывается в данные. В этом случае уменьшение параметра сглаживания от значения по умолчанию создает кривую, которая еще более сглажена, но не соответствует данным. По мере увеличения параметра сглаживания за пределы значения по умолчанию связанная кривая приближается к интерполятору кубического сплайна. Кубический сплайн и сглаживающий сплайн по умолчанию аналогичны для внутренних точек, но расходятся в конечных точках.