Первым шагом создания и обучения новой сверточной нейронной сети (ConvNet) является определение архитектуры сети. В этом разделе описываются подробные сведения о слоях ConvNet и порядок их отображения в ConvNet. Полный список слоев глубокого обучения и способы их создания см. в разделе Список слоев глубокого обучения. Сведения о сетях LSTM для классификации последовательностей и регрессии см. в разделе Сети долговременной памяти. Сведения о создании собственных пользовательских слоев см. в разделе Определение пользовательских слоев глубокого обучения.
Архитектура сети может варьироваться в зависимости от типов и количества включенных уровней. Типы и количество включенных уровней зависят от конкретного приложения или данных. Например, при наличии категориальных ответов необходимо иметь уровень softmax и уровень классификации, тогда как при непрерывном ответе в конце сети должен быть уровень регрессии. Меньшей сети с одним или двумя сверточными слоями может быть достаточно для изучения небольшого количества данных изображения в градациях серого. С другой стороны, для более сложных данных с миллионами цветных изображений может потребоваться более сложная сеть с несколькими сверточными и полностью соединенными слоями.
Чтобы задать архитектуру глубокой сети с последовательным подключением всех слоев, создайте массив слоев напрямую. Например, чтобы создать глубокую сеть, которая классифицирует изображения 28 на 28 в градациях серого в классы 10, укажите массив слоев.
layers = [
imageInputLayer([28 28 1])
convolution2dLayer(3,16,'Padding',1)
batchNormalizationLayer
reluLayer
maxPooling2dLayer(2,'Stride',2)
convolution2dLayer(3,32,'Padding',1)
batchNormalizationLayer
reluLayer
fullyConnectedLayer(10)
softmaxLayer
classificationLayer];layers является массивом Layer объекты. Затем можно использовать layers в качестве входных данных для функции обучения trainNetwork.Чтобы задать архитектуру нейронной сети со всеми слоями, соединенными последовательно, создайте массив слоев напрямую. Чтобы задать архитектуру сети, в которой уровни могут иметь несколько входов или выходов, используйте LayerGraph объект.
Создание слоя ввода изображения с помощью imageInputLayer.
Уровень ввода изображения вводит изображения в сеть и применяет нормализацию данных.
Укажите размер изображения с помощью inputSize аргумент. Размер изображения соответствует высоте, ширине и количеству цветовых каналов этого изображения. Например, для изображения в градациях серого число каналов равно 1, а для цветного изображения - 3.
2-D сверточный слой применяет скользящие сверточные фильтры к входу. Создание 2-D сверточного слоя с помощью convolution2dLayer.
Сверточный слой состоит из различных компонентов. [1 ]
Сверточный слой состоит из нейронов, которые соединяются с субрегионами входных изображений или выходами предыдущего уровня. Слой изучает элементы, локализованные этими областями, при сканировании изображения. При создании слоя с помощью convolution2dLayer , можно указать размер этих областей с помощью filterSize входной аргумент.
Для каждого региона trainNetwork функция вычисляет скалярное произведение весов и входных данных, а затем добавляет член смещения. Набор весов, который применяется к области изображения, называется фильтром. Фильтр перемещается по входному изображению вертикально и горизонтально, повторяя одни и те же вычисления для каждой области. Другими словами, фильтр свертывает входной сигнал.
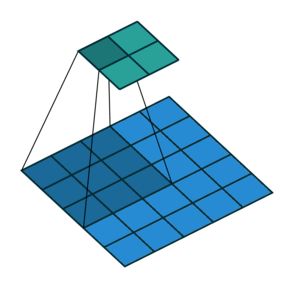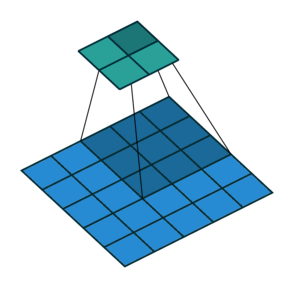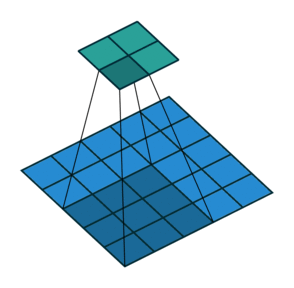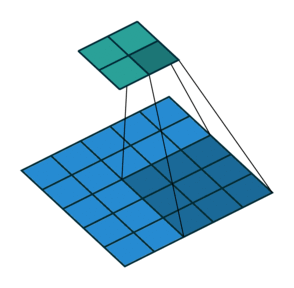
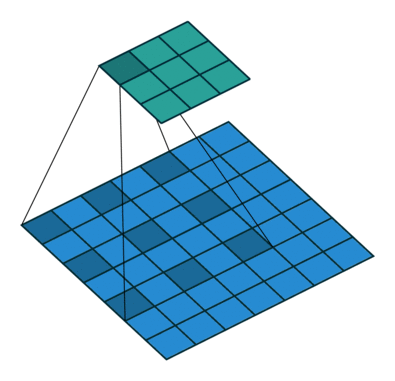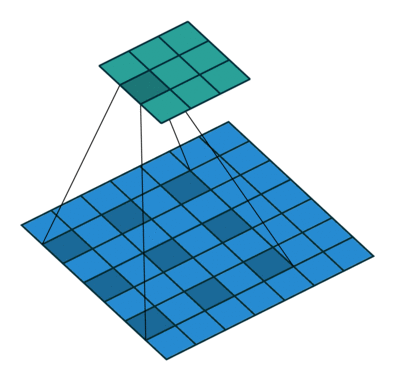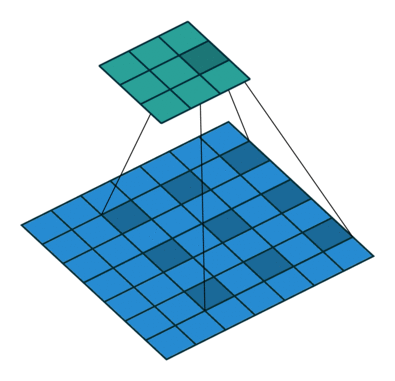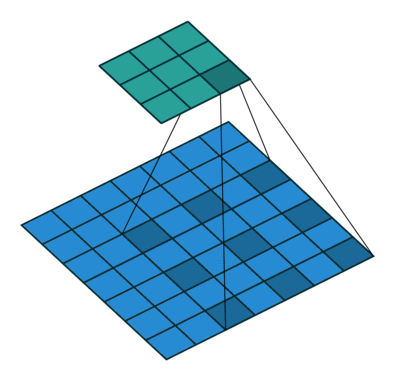
На этом рисунке показано сканирование фильтра 3 на 3 через вход. Нижняя карта представляет входные данные, а верхняя карта представляет выходные данные.
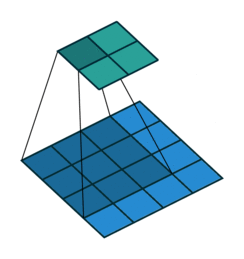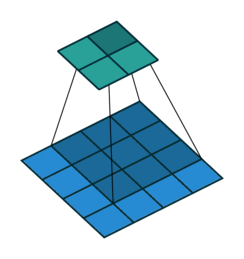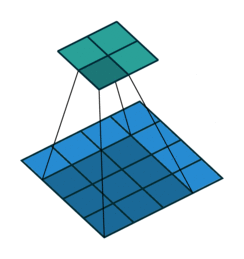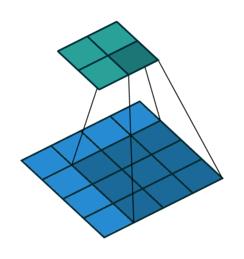
Размер шага, с которым перемещается фильтр, называется шагом. Размер шага можно указать с помощью Stride аргумент пары имя-значение. Локальные области, с которыми соединяются нейроны, могут перекрываться в зависимости от filterSize и 'Stride' значения.
На этом рисунке показано сканирование фильтра 3 на 3 через вход с шагом 2. Нижняя карта представляет входные данные, а верхняя карта представляет выходные данные.
Число весов в фильтре равно h * w * c, где h - высота, а w - ширина фильтра соответственно, а c - количество каналов на входе. Например, если вход представляет собой цветное изображение, количество цветовых каналов равно 3. Количество фильтров определяет количество каналов на выходе сверточного уровня. Укажите количество фильтров с помощью numFilters аргумент с convolution2dLayer функция.
Расширенный сверток - это сверток, в котором фильтры расширены промежутками, вставленными между элементами фильтра. Укажите коэффициент расширения с помощью 'DilationFactor' собственность.
Используйте расширенные свертки для увеличения воспринимающего поля (области входа, которую может видеть слой) слоя без увеличения количества параметров или вычислений.
Слой расширяет фильтры, вставляя нули между каждым элементом фильтра. Коэффициент расширения определяет размер шага для выборки входного сигнала или эквивалентный коэффициент повышения дискретизации фильтра. Он соответствует эффективному размеру фильтра (размер фильтра - 1). * Коэффициент расширения + 1. Например, фильтр 3 на 3 с коэффициентом расширения [2 2] эквивалентен фильтру 5 на 5 с нулями между элементами.
На этом рисунке показан фильтр 3 на 3, расширенный в два раза при сканировании через вход. Нижняя карта представляет входные данные, а верхняя карта представляет выходные данные.
Когда фильтр перемещается по входному сигналу, он использует тот же набор весов и то же смещение для свертки, образуя карту элементов. Каждая карта элементов является результатом свертки, использующей различный набор весов и различное смещение. Следовательно, количество карт признаков равно количеству фильтров. Общее число параметров в сверточном слое равно ((h * w * c + 1) * Число фильтров), где 1 - смещение.
Можно также применить заполнение к границам входного изображения по вертикали и горизонтали с помощью 'Padding' аргумент пары имя-значение. Заполнение - это значения, добавляемые к границам входных данных для увеличения их размера. Настраивая заполнение, можно управлять размером вывода слоя.
На этом рисунке показано сканирование фильтра 3 на 3 через вход с заполнением размера 1. Нижняя карта представляет входные данные, а верхняя карта представляет выходные данные.
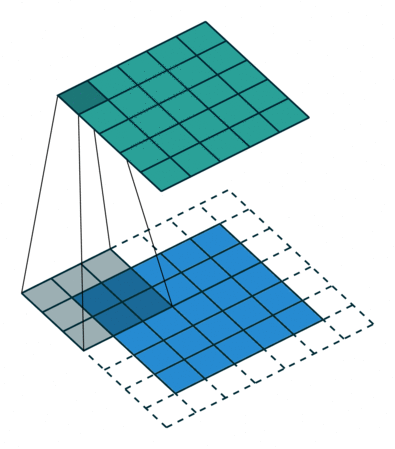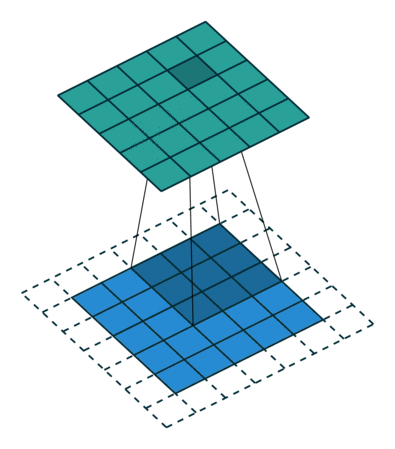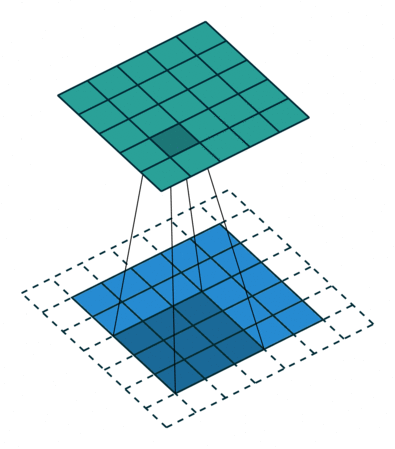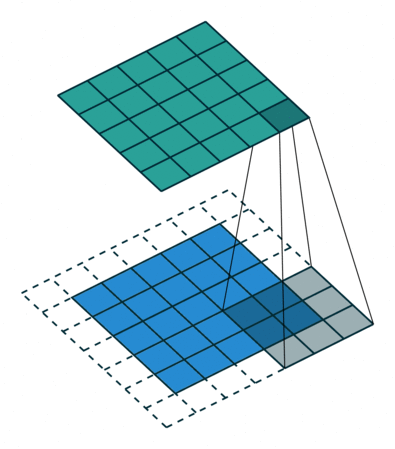
Высота и ширина вывода сверточного слоя: (Входной размер - ((Размер фильтра - 1) * Коэффициент расширения + 1) + 2 * Заполнение )/Stride + 1. Это значение должно быть целым числом для полного охвата всего изображения. Если сочетание этих опций не приводит к полному закрытию изображения, программа по умолчанию игнорирует оставшуюся часть изображения вдоль правого и нижнего краев свертки.
Произведение выходной высоты и ширины дает общее количество нейронов в карте признаков, скажем, размер карты. Общее количество нейронов (выходной размер) в сверточном слое - Map Size * Number of Filters.
Например, предположите, что входное изображение - цветное изображение 32 на 32 на 3. Для сверточного слоя с восемью фильтрами и размером фильтра 5 на 5 количество весов на фильтр равно 5 * 5 * 3 = 75, а общее количество параметров в слое равно (75 + 1) * 8 = 608. Если шаг 2 в каждом направлении и задана заливка размера 2, то каждая карта элементов имеет значение 16 на 16. Это происходит потому, что (32 - 5 + 2 * 2 )/2 + 1 = 16,5, и часть крайнего заполнения справа и снизу изображения отбрасывается. Наконец, общее количество нейронов в слое составляет 16 * 16 * 8 = 2048.
Обычно результаты этих нейронов проходят через некоторую форму нелинейности, такую как выпрямленные линейные единицы (ReLU).
При определении сверточного уровня можно настроить скорость обучения и параметры регуляризации для слоя с помощью аргументов пары имя-значение. Если эти параметры не указаны, то trainNetwork использует глобальные варианты обучения, определенные с помощью trainingOptions функция. Дополнительные сведения о глобальных параметрах и параметрах обучения на уровне см. в разделе Настройка параметров и сверточная нейронная сеть поезда.
Сверточная нейронная сеть может состоять из одного или нескольких сверточных слоев. Количество сверточных слоев зависит от количества и сложности данных.
Создание уровня нормализации пакета с помощью batchNormalizationLayer.
Уровень пакетной нормализации нормализует мини-пакет данных по всем наблюдениям для каждого канала независимо. Чтобы ускорить обучение сверточной нейронной сети и снизить чувствительность к инициализации сети, используйте уровни пакетной нормализации между сверточными слоями и нелинейностями, такими как уровни ReLU.
Слой сначала нормализует активации каждого канала путем вычитания среднего значения мини-партии и деления на стандартное отклонение мини-партии. Затем слой сдвигает входной сигнал на обучаемое смещение β и масштабирует его на обучаемый масштабный коэффициент γ. β и γ сами по себе являются обучаемыми параметрами, которые обновляются во время обучения сети.
Пакетные уровни нормализации нормализуют активации и градиенты, распространяющиеся через нейронную сеть, что делает обучение сети более простой задачей оптимизации. Чтобы в полной мере воспользоваться этим фактом, вы можете попробовать увеличить скорость обучения. Поскольку проблема оптимизации проще, обновления параметров могут быть больше, и сеть может учиться быстрее. Также можно попытаться уменьшить L2 и регуляризацию отсева. При использовании слоев нормализации партии активация определенного изображения во время обучения зависит от того, какие изображения появятся в той же самой мини-партии. Чтобы в полной мере воспользоваться этим регуляризирующим эффектом, попробуйте перетасовать данные обучения перед каждой эпохой обучения. Чтобы указать частоту перетасовки данных во время обучения, используйте 'Shuffle' аргумент пары имя-значение trainingOptions.
Создание слоя ReLU с помощью reluLayer.
Уровень ReLU выполняет пороговую операцию для каждого элемента входа, где любое значение меньше нуля устанавливается равным нулю.
За сверточным и пакетным уровнями нормализации обычно следует нелинейная функция активации, такая как выпрямленная линейная единица (ReLU), заданная уровнем ReLU. Уровень ReLU выполняет пороговую операцию для каждого элемента, где любое входное значение меньше нуля устанавливается равным нулю, то есть
={x,x≥00,x<0.
Уровень ReLU не изменяет размер своего входа.
Существуют другие нелинейные уровни активации, которые выполняют различные операции и могут повысить точность сети для некоторых приложений. Список уровней активации см. в разделе Слои активации.
Создание уровня нормализации кросс-каналов с помощью crossChannelNormalizationLayer.
Канальный уровень локальной (кросс-канальной) нормализации выполняет канальную нормализацию.
Этот уровень выполняет нормализацию локального отклика по каналам. Обычно он следует за уровнем активации ReLU. Этот слой заменяет каждый элемент нормированным значением, которое он получает, используя элементы из определенного числа соседних каналов (элементы в окне нормализации). То есть для каждого элемента на входе, trainNetwork вычисляет нормализованное значение 'с помощью
sswindowStartSize) β,
где K, α и β - гиперпараметры в нормализации, а ss - сумма квадратов элементов в окне нормализации [2]. Необходимо указать размер окна нормализации с помощью windowChannelSize аргумент crossChannelNormalizationLayer функция. Можно также указать гиперпараметры с помощью Alpha, Beta, и K аргументы пары имя-значение.
Предыдущая формула нормализации несколько отличается от приведенной в [2]. Эквивалентную формулу можно получить, умножив alpha значение по windowChannelSize.
Уровень максимального объединения выполняет понижающую дискретизацию путем разделения входных данных на прямоугольные области объединения и вычисления максимума каждой области. Создание максимального уровня пула с помощью maxPooling2dLayer.
Средний уровень объединения выполняет понижающую дискретизацию путем разделения входных данных на прямоугольные области объединения и вычисления средних значений каждой области. Создание среднего уровня пула с помощью averagePooling2dLayer.
Слои объединения следуют за сверточными слоями для понижающей выборки, следовательно, уменьшая количество соединений со следующими слоями. Они не выполняют обучение самостоятельно, но уменьшают количество параметров, подлежащих изучению на следующих уровнях. Они также помогают уменьшить переоборудование.
Слой максимального объединения возвращает максимальные значения прямоугольных областей своего входа. Размер прямоугольных областей определяется poolSize аргумент maxPoolingLayer. Например, если poolSize равняется [2,3]затем слой возвращает максимальное значение в областях высоты 2 и ширины 3. Средний слой объединения выводит средние значения прямоугольных областей своего входа. Размер прямоугольных областей определяется poolSize аргумент averagePoolingLayer. Например, если poolSize равно [2,3], то слой возвращает среднее значение областей высоты 2 и ширины 3.
Слои пула сканируют входные данные по горизонтали и вертикали в размерах шагов, которые можно указать с помощью 'Stride' аргумент пары имя-значение. Если размер пула меньше или равен шагу, то области объединения не перекрываются.
Для неперекрывающихся областей (размер пула и Stride равны), если вход на уровень объединения равен n-by-n, а размер области объединения равен h-by-h, то уровень объединения выполняет выборку областей по h [6]. То есть выходной сигнал максимального или среднего уровня объединения для одного канала сверточного уровня равен n/h-by-n/h. Для перекрывающихся областей выходом уровня объединения является (Input Size - Pool Size + 2 * Padding )/Stride + 1.
Создание слоя отсева с помощью dropoutLayer.
Уровень отсева случайным образом устанавливает входные элементы в ноль с заданной вероятностью.
Во время тренировки слой случайным образом устанавливает входные элементы в нуль, заданный маской отсева rand(size(X))<Probability, где X является вводимым слоем, а затем масштабирует остальные элементы на 1/(1-Probability). Эта операция эффективно изменяет базовую сетевую архитектуру между итерациями и предотвращает переполнение сети [7], [2]. Большее число приводит к тому, что во время обучения сбрасывается больше элементов. Во время предсказания выходной сигнал слоя равен его входному сигналу.
Аналогично максимальному или среднему уровню объединения, обучение на этом уровне не происходит.
Создание полностью подключенного слоя с помощью fullyConnectedLayer.
Полностью связанный слой умножает входной сигнал на весовую матрицу и затем добавляет вектор смещения.
За сверточными (и нисходящими) слоями следует один или более полностью соединенных слоев.
Как следует из названия, все нейроны в полностью связанном слое соединяются со всеми нейронами в предыдущем слое. Этот слой объединяет все элементы (локальную информацию), полученные предыдущими слоями по изображению, чтобы идентифицировать более крупные массивы. Для проблем классификации последний полностью подключенный слой объединяет элементы для классификации изображений. Это причина того, что outputSize аргумент последнего полностью подключенного уровня сети равен числу классов набора данных. Для проблем регрессии размер выходного сигнала должен быть равен числу переменных отклика.
Можно также настроить скорость обучения и параметры регуляризации для этого уровня, используя связанные аргументы пары имя-значение при создании полностью связанного уровня. Если вы решите не корректировать их, то trainNetwork использует глобальные параметры обучения, определенные trainingOptions функция. Дополнительные сведения о глобальных параметрах и параметрах обучения на уровне см. в разделе Настройка параметров и сверточная нейронная сеть поезда.
Полностью соединенный слой умножает входной сигнал на весовую матрицу W и затем добавляет вектор смещения b.
Если вход на уровень является последовательностью (например, в сети LSTM), то полностью подключенный уровень действует независимо на каждом временном шаге. Например, если слой перед полностью соединенным слоем выводит матрицу X размера D-by-N-by-S, то полностью соединенный слой выводит матрицу Z размера outputSize-by-N-by-S. На временном шаге t соответствующей записью Z является b, Xt обозначает временной шаг t X.
Уровень softmax применяет функцию softmax к входу. Создание уровня softmax с помощью softmaxLayer.
Уровень классификации вычисляет потери перекрестной энтропии для задач классификации и взвешенной классификации с взаимоисключающими классами. Создание классификационного слоя с помощью classificationLayer.
Для проблем классификации уровень softmax и затем уровень классификации должны следовать за окончательным полностью подключенным уровнем.
Функция активации выходного блока представляет собой функцию softmax:
aj (x)),
где и .
Функция softmax является функцией активации выходного блока после последнего полностью подключенного уровня для проблем классификации нескольких классов:
∑j=1kexp (aj (x, θ)),
где ≤1 start) = 1. cr)), P (x, start' cr) - условная вероятность выборки класса r, а P (cr) - предшествующая вероятность класса.
Функция softmax также известна как нормированная экспоненциальная и может считаться мультиклассовым обобщением логистической сигмоидной функции [8].
Для типовых классификационных сетей уровень классификации должен соответствовать уровню softmax. В классификационном слое trainNetwork берет значения из функции softmax и присваивает каждый вход одному из K взаимоисключающих классов, используя функцию перекрестной энтропии для 1-of-K схемы кодирования [8]:
где N - число выборок, K - число классов, - вес для класса i, - индикатор того, что n-я выборка принадлежит i-му классу, и - выходной сигнал для выборки n для класса i, который в данном случае является значением из функции softmax. Другими словами, - это вероятность того, что сеть связывает n-й вход с классом i.
Создание регрессионного слоя с помощью regressionLayer.
Уровень регрессии вычисляет потери в полусреднем квадрате для задач регрессии. Для типичных проблем регрессии уровень регрессии должен следовать за окончательным полностью соединенным слоем.
Для одного наблюдения среднеквадратичная ошибка задается следующим образом:
2R,
где R - количество откликов, ti - целевой выходной сигнал, и yi - предсказание сети для отклика i.
Для регрессионных сетей «изображение - последовательность - один» функция потерь регрессионного слоя представляет собой среднеквадратичную ошибку прогнозируемых откликов, не нормализованную по R:
) 2.
Для регрессионных сетей «изображение-изображение» функция потерь регрессионного слоя представляет собой половину среднеквадратичной ошибки прогнозируемых откликов для каждого пикселя, не нормализованную по R:
) 2,
где H, W и C обозначают высоту, ширину и количество каналов выхода, соответственно, и p-индексы в каждом элементе (пикселе) t и y линейно.
Для регрессионных сетей «последовательность-последовательность» функция потерь регрессионного слоя представляет собой половину среднеквадратичной ошибки прогнозируемых откликов для каждого временного шага, не нормализованную по R:
) 2,
где S - длина последовательности.
При обучении программное обеспечение вычисляет средние потери по наблюдениям в мини-партии.
[1] Мерфи, К. П. Машинное обучение: вероятностная перспектива. Кембридж, Массачусетс: MIT Press, 2012.
[2] Крижевский, А., И. Суцкевер, Г. Э. Хинтон. «ImageNet Classification с глубокими сверточными нейронными сетями». Достижения в системах обработки нейронной информации. Том 25, 2012.
[3] LeCun, Y., Boser, B., Denker, J.S., Хендерсон, D., Говард, R.E., Хаббард, W., Jackel, L.D., и др. «Распознавание рукописных цифр с помощью сети обратного распространения». In Advances of Neural Information Processing Systems, 1990.
[4] LeCun, Y., L. Bottou, Y. Bengio и P. Haffner. «Градиентное обучение, применяемое к распознаванию документов». Процедуры IEEE. Том 86, стр. 2278-2324, 1998.
[5] Наир, В. и Г. Э. Хинтон. «Выпрямленные линейные блоки улучшают ограниченную работу машин boltzmann». В Proc. 27-я Международная конференция по машинному обучению, 2010.
[6] Наги, Дж., Ф. Дюкатель, Г. А. Ди Каро, Д. Сиресан, У. Мейер, А. Джусти, Ф. Наги, Дж. Шмидхубер, Л. М. Гамбарделла. «Макс. объединение сверточных нейронных сетей для распознавания жестов рук на основе зрения». Международная конференция IEEE по применению обработки сигналов и изображений (ICSIPA2011), 2011.
[7] Шривастава, Н., Г. Хинтон, А. Крижевский, И. Суцкевер, Р. Салахутдинов. «Отсев: простой способ предотвратить переоснащение нейронных сетей». Журнал исследований машинного обучения. Том 15, стр. 1929 - 1958, 2014.
[8] Бишоп, К. М. Распознавание образов и машинное обучение. Спрингер, Нью-Йорк, Нью-Йорк, 2006.
[9] Иоффе, Сергей и Кристиан Сегеди. «Пакетная нормализация: ускорение глубокого обучения сети путем уменьшения внутреннего ковариатного сдвига». препринт, arXiv:1502.03167 (2015).
averagePooling2dLayer | batchNormalizationLayer | classificationLayer | clippedReluLayer | convolution2dLayer | crossChannelNormalizationLayer | dropoutLayer | fullyConnectedLayer | imageInputLayer | leakyReluLayer | maxPooling2dLayer | regressionLayer | reluLayer | softmaxLayer | trainingOptions | trainNetwork
[1] Кредит изображения: арифметика свертки (лицензия)