БПФ высокого разрешения части спектра
dsp.ZoomFFT Система object™ вычисляет быстрое преобразование Фурье (БПФ) сигнала на части частот в интервале Найквиста. Путем установки соответствующего коэффициента прореживания D и частоты дискретизации Fs можно выбрать полосу частот для анализа BW, где BW = Fs/D. Можно также выбрать определенный диапазон частот для анализа в интервале Найквиста, выбрав центральную частоту нужного диапазона.
Разрешающей способностью сигнала является отношение Fs и длины БПФ (L). С помощью масштабирования БПФ можно сохранить то же разрешение, что и при полноразмерном БПФ исходного сигнала, вычисляя небольшой БПФ для более короткого сигнала. Более короткий сигнал исходит от прореживания исходного сигнала. Экономия достигается за счет возможности вычисления гораздо более короткого БПФ при достижении того же разрешения. Для коэффициента прореживания D новая частота дискретизации Fsd равна Fs/D, а новый размер кадра (и длина FFT) равна Ld = L/D. Разрешение прореженного сигнала Fsd/Ld = Fs/L. Для достижения более высокого разрешения более короткой полосы используется исходная длина БПФ L вместо прореженной длины БПФ Ld.
Для вычисления БПФ части спектра:
Создать dsp.ZoomFFT и задайте его свойства.
Вызовите объект с аргументами, как если бы это была функция.
Дополнительные сведения о работе системных объектов см. в разделе Что такое системные объекты?.
zfft = dsp.ZoomFFTzfft, которая выполняет БПФ на части частотного диапазона входного сигнала. Объект определяет диапазон частот для выполнения БПФ с использованием заданных значений центральной частоты и коэффициента прореживания.
zfft = dsp.ZoomFFT(d)d.
zfft = dsp.ZoomFFT(d,Fc)d, и свойству StartFrequency присвоено значение Fc.
zfft = dsp.ZoomFFT(d,Fc,Fs)d, для свойства StartFrequency установлено значение Fcи свойство SampleRate имеет значение Fs.
zfft = dsp.ZoomFFT(Name,Value)
zfft = dsp.ZoomFFT(2,2e3,48e3,'FFTLength',64);Чтобы использовать функцию объекта, укажите объект System в качестве первого входного аргумента. Например, для освобождения системных ресурсов объекта System с именем obj, используйте следующий синтаксис:
release(obj)
Вычислите БПФ поддиапазона [1500 Гц 2500 Гц] с помощью масштабирования БПФ для сигнала, дискретизированного на частоте 48 кГц.
Инициализация
Установите центральную частоту 2 кГц, а полосу пропускания 1 кГц. Полоса пропускания центрируется на центральной частоте. Коэффициент прореживания представляет собой отношение входной частоты дискретизации, 48 кГц, и представляющей интерес полосы пропускания, 1 кГц. Выберите длину БПФ 64. Задайте размер входного кадра как коэффициент прореживания, умноженный на длину БПФ. Создать dsp.ZoomFFT объект с заданным коэффициентом прореживания, центральной частотой, частотой дискретизации и длиной БПФ.
Fs = 48e3;
CF = 2e3;
BW = 1e3;
D = Fs/BW;
fftlen = 64;
L = D * fftlen;
zfft = dsp.ZoomFFT(D,CF,Fs,'FFTLength',fftlen);
Частоты
БПФ вычисляется по частотам, начинающимся на 1500 Гц и разнесенным на $ Fs/( D * fftLen) $ Гц, что является разрешением или минимальной частотой, которую можно различить. Число частот, на которых вычисляется увеличение БПФ, равно длине БПФ.
Fsd = Fs/D; F = CF + (Fsd/fftlen)*(0:fftlen-1)-Fsd/2;
Инициализация области
Создание графика массива для отображения частот в F.
ap = dsp.ArrayPlot('XDataMode','Custom','CustomXData',F,... 'YLabel','z .* conj(z)','XLabel','Frequency (Hz)','YLimits',[0 1.1e3],... 'Title',sprintf('Decimation Factor = %d. Center Frequency = %d Hz. Resolution = %f Hz',D, CF,(Fs/D)/fftlen));
Генератор синусоидальных волн
Создайте синусоидальную волну с частотами 1625 Гц, 2000 Гц и 2125 Гц.
tones = [1625 2000 2125]; sine = dsp.SineWave('SampleRate',Fs,'Frequency',tones,'SamplesPerFrame',L);
Вытекание
Пропускают шумную синусоидальную волну с частотой дискретизации 48 кГц. Вычислите масштаб БПФ этой синусоидальной волны в поддиапазоне [1500 Гц 2500 Гц]. Переупорядочить преобразование Фурье, сдвинув нулевую частотную составляющую в центр массива. На графике массива просмотрите тональные сигналы с частотой 1625 Гц, 2000 Гц и 2125 Гц.
for i = 1:1000 x = sum(sine(),2)+1e-1*randn(L,1); z = zfft(x); z = fftshift(z); ap(z.*conj(z)); end
dsp.ZoomFFT объект принимает входные данные переменного размера, если входные данные кратны коэффициенту прореживания. Количество входных каналов не может изменяться.
Создать dsp.ZoomFFT объект с коэффициентом прореживания 4, центральной частотой 2 кГц и частотой входных выборок 48 кГц. Передача случайного ввода с 4 * 64 строками и 2 столбцами. Измените число строк на 4 * 128 и 4 * 32. Результирующие длины БПФ равны 64, 128 и 32 соответственно. Размер выходных сигналов равен [64 2], [128 2] и [32 2] соответственно.
zfft = dsp.ZoomFFT(4,2e3,48e3); y1 = zfft(randn(4*64,2)); y2 = zfft(randn(4*128,2)); y3 = zfft(randn(4*32,2));
Задайте длину БПФ 256 и передайте входные данные переменного размера. Размер всех выходов - [256 2].
release(zfft); zfft.FFTLength = 256; y4 = zfft(randn(4*64,2)); y5 = zfft(randn(4*128,2)); y6 = zfft(randn(4*32,2));
Алгоритм масштабирования БПФ использует полосовую фильтрацию перед вычислением БПФ сигнала. Концепция полосовой фильтрации заключается в том, что предполагается, что вы заинтересованы в полосе [F1, F2] исходного входного сигнала, дискретизированного со скоростью Fs Гц. Если пройти этот сигнал через комплексный (односторонний) полосовой фильтр, центрированный на Fc = (F1 + F2 )/2, с полосой пропускания BW = F2 - F1, а затем понизить оценку сигнала на коэффициент D = floor (Fs/BW), требуемая полоса падает до основной полосы.
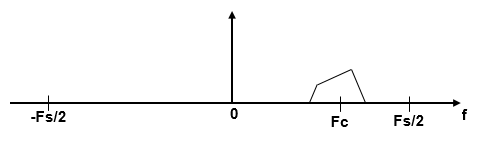
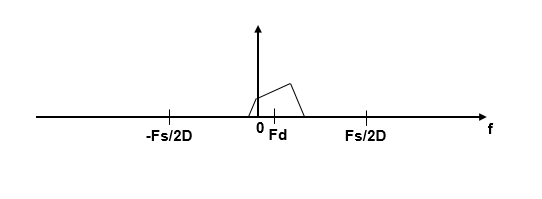
Если Fc не может быть выражена в виде k × Fs/D, где k - целое число, то сдвинутый, прореженный спектр не центрируется при DC. В этом случае центральная частота преобразуется в Fd.
+ Fs/2 )/Fs)
Комплексный полосовой фильтр получают, сначала проектируя прототип фильтра нижних частот, а затем умножая коэффициенты нижних частот на комплексный экспоненциальный. Этот алгоритм использует многоступенчатый фильтр FIR в качестве прототипа фильтра нижних частот. Для получения полосового фильтра коэффициенты каждого каскада сдвигаются по частоте. Коэффициент прореживания является кумулятивным коэффициентом прореживания каждого этапа. Сложные полосовые фильтры, за которыми следует прореживатель, реализуются с использованием эффективной полифазной структуры. Для получения дополнительной информации о конструкции сложного полосового фильтра из многоступенчатого многоступенчатого фильтра FIR см. Zoom FFT и Complex Bandpass Filter Design.
[1] Харрис, F.J. Многоскоростная обработка сигналов для систем связи. Prentice Hall, 2004, стр. 208-209.