Прогнозные отклики байесовской модели линейной регрессии
yF = forecast(Mdl,XF)numPeriods прогнозируемые ответы из байесовской модели линейной регрессии
Mdl учитывая данные предиктора в XF, матрица с numPeriods строк.
Чтобы оценить прогноз, forecast использует среднее значение numPeriods-мерное апостериорное прогностическое распределение.
Если Mdl является совместной предыдущей моделью (возвращается bayeslm), то forecast использует только совместное предыдущее распределение и инновационное распределение для формирования прогностического распределения.
Если Mdl является задней моделью (возвращается estimate), то forecast использует апостериорное прогностическое распределение.
NaNs в данных указывают отсутствующие значения, которые forecast удаляет, используя удаление по списку.
yF = forecast(Mdl,XF,X,y)X и соответствующие данные ответа y.
Если Mdl является совместной предшествующей моделью, то forecast создает апостериорное прогностическое распределение путем обновления предшествующей модели информацией о параметрах, которые она получает из данных.
Если Mdl является задней моделью, то forecast обновляет апостериоры информацией о параметрах, которые они получают из дополнительных данных. Полная вероятность данных состоит из дополнительных данных. X и yи данные, которые были созданы Mdl.
yF = forecast(___,Name,Value)
Если Mdl является empiricalblm объект модели, то вы не можете указать Beta или Sigma2. Нельзя прогнозировать из условных предиктивных распределений с помощью эмпирического предыдущего распределения.
Моделирование Монте-Карло подвержено изменению. Если forecast использует моделирование Монте-Карло, тогда оценки и выводы могут различаться при вызове forecast многократно при, казалось бы, эквивалентных условиях. Чтобы воспроизвести результаты оценки, установите начальное число случайного числа с помощью rng перед вызовом forecast.
Если forecast выдает ошибку при оценке апостериорного распределения с использованием пользовательской предыдущей модели, затем попробуйте скорректировать начальные значения параметров с помощью BetaStart или Sigma2Startили попробуйте изменить объявленную функцию log previous, а затем восстановить модель. Ошибка может указывать на то, что журнал предыдущего распространения –Inf при заданных исходных значениях.
Для прогнозируемых ответов от условного апостериорного прогностического распределения аналитически труднореализуемых моделей, за исключением эмпирических моделей, передайте свой предыдущий объект модели и данные выборки оценки в forecast. Затем укажите Beta аргумент пары «имя-значение» для прогнозирования из условного заднебокового значения Sigma2 аргумент пары «имя-значение» для прогнозирования из условной задней части β.
Каждый раз, когда forecast должен оценить апостериорное распределение (например, когда Mdl представляет собой предыдущее распределение, и вы поставляете X и y) и задняя является аналитически отслеживаемой, forecast оценивает решения закрытой формы для оценщиков Байеса. В противном случае forecast прибегает к моделированию Монте-Карло для прогнозирования с использованием заднего прогностического распределения. Дополнительные сведения см. в разделе Апостериорная оценка и вывод.
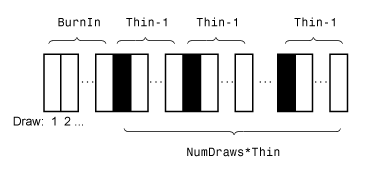
На этом рисунке показано, как forecast уменьшает выборку Монте-Карло, используя значения NumDraws, Thin, и BurnIn. Прямоугольники представляют последовательные розыгрыши из распределения. forecast удаляет белые прямоугольники из образца Монте-Карло. Остающееся NumDraws черные прямоугольники составляют образец Монте-Карло.
conjugateblm | customblm | diffuseblm | empiricalblm | lassoblm | mixconjugateblm | mixsemiconjugateblm | semiconjugateblm