Exponenta Banner
exponenta event banner

оценка

Оценка апостериорного распределения параметров модели байесовской линейной регрессии

свернуть все на странице

Синтаксис

PoseMdl = оценка (PriorMdl, X, y)
PoseMdl = оценка (PriorMdl, X, y, имя, значение)
[PoseMdl, Summary] = оценка (___)

Описание

Чтобы выполнить выбор переменных предиктора для байесовской модели линейной регрессии, см. раздел estimate.

пример

PosteriorMdl = estimate(PriorMdl,X,y) возвращает модель байесовской линейной регрессии PosteriorMdl что характеризует спаренные апостериорные распределения коэффициентов β и дисперсию возмущений start2. PriorMdl определяет совместное предварительное распределение параметров и структуру модели линейной регрессии. X является данными предиктора и y - данные ответа. PriorMdl и PosteriorMdl возможно, это не тот же тип объекта.

Произвести PosteriorMdl, estimate функция обновляет предыдущее распределение информацией о параметрах, которые она получает из данных.

NaNs в данных указывают отсутствующие значения, которые estimate удаляет, используя удаление по списку.

пример

PosteriorMdl = estimate(PriorMdl,X,y,Name,Value) указывает дополнительные параметры, использующие один или несколько аргументов пары имя-значение. Например, для оценки условного апостериорного распределения одного параметра, учитывая заданное значение другого параметра, можно задать значение либо для β, либо для start2.

При указании Beta или Sigma2 аргумент пары имя-значение, затем PosteriorMdl и PriorMdl равны.

пример

[PosteriorMdl,Summary] = estimate(___) использует любую из комбинаций входных аргументов в предыдущих синтаксисах для возврата таблицы, которая содержит для каждого параметра следующее: заднее среднее и стандартное отклонение, 95% достоверный интервал, заднюю вероятность того, что параметр больше 0, и описание заднего распределения (если таковое существует). Также в таблице содержится задняя ковариационная матрица β и start2. При указании Beta или Sigma2 аргумент пары имя-значение, затем estimate возвращает условные апостериорные оценки.

Примеры

свернуть все

Открыть сценарий в реальном времени

Рассмотрим модель, которая предсказывает экономию топлива (в МПГ) автомобиля, учитывая его рабочий объем и вес.

Загрузить carsmall набор данных.

load carsmall
x = [Displacement Weight];
y = MPG;

Регресс экономии топлива на рабочий объем и вес двигателя, включая перехват для получения оценок обычных наименьших квадратов (OLS).

Mdl = fitlm(x,y)
Mdl = 
Linear regression model:
    y ~ 1 + x1 + x2

Estimated Coefficients:
                    Estimate        SE         tStat       pValue  
                   __________    _________    _______    __________

    (Intercept)        46.925       2.0858     22.497    6.0509e-39
    x1              -0.014593    0.0082695    -1.7647      0.080968
    x2             -0.0068422    0.0011337    -6.0353    3.3838e-08


Number of observations: 94, Error degrees of freedom: 91
Root Mean Squared Error: 4.09
R-squared: 0.747,  Adjusted R-Squared: 0.741
F-statistic vs. constant model: 134, p-value = 7.22e-28

Mdl.MSE
ans = 16.7100

Создайте по умолчанию диффузное предварительное распределение для одного предиктора.

p = 2;
PriorMdl = bayeslm(p);

PriorMdl является diffuseblm объект модели.

Используйте опции по умолчанию, чтобы оценить апостериорное распределение.

PosteriorMdl = estimate(PriorMdl,x,y);
Method: Analytic posterior distributions
Number of observations: 94
Number of predictors:   3
 
           |   Mean     Std         CI95        Positive       Distribution     
--------------------------------------------------------------------------------
 Intercept | 46.9247  2.1091  [42.782, 51.068]    1.000   t (46.92, 2.09^2, 91) 
 Beta(1)   | -0.0146  0.0084  [-0.031,  0.002]    0.040   t (-0.01, 0.01^2, 91) 
 Beta(2)   | -0.0068  0.0011  [-0.009, -0.005]    0.000   t (-0.01, 0.00^2, 91) 
 Sigma2    | 17.0855  2.5905  [12.748, 22.866]    1.000   IG(45.50, 0.0013)

PosteriorMdl является conjugateblm объект модели.

Задние средства и оценки коэффициента ОЛС почти идентичны. Также задние стандартные отклонения и стандартные ошибки ОЛС почти идентичны. Заднее среднее Sigma2 близок к среднеквадратичной ошибке (MSE) ОЛС.

Открыть сценарий

Рассмотрим модель множественной линейной регрессии, которая предсказывает реальный валовой национальный продукт США (GNPR) с использованием линейной комбинации суммарной занятости (E) и реальная заработная плата (WR).

$$\texttt{GNPR}_t=\beta_0+\beta_2\texttt{E}_t+\beta_3\texttt{WR}_t+\varepsilon_t.$$

Для всех $t$$\varepsilon_t$представляет собой ряд независимых гауссовых возмущений со средним значением 0 и дисперсией. $\sigma^2$Предположим, что эти предыдущие распределения:

  • $\beta_j\vert\sigma^2$ - распределение 3-D t с 10 степенями свободы для каждого компонента, корреляционная матрица C, местоположение ct, и масштаб st.

  • $\sigma^2 \sim IG(r_1,r_2)$, с формой$r_1$ и масштабом.$r_2$

bayeslm рассматривает эти предположения и вероятность данных, как если бы соответствующий задний является аналитически труднореализуемым.

Объявите функцию MATLAB ®, которая:

  • Принимает значения$\beta$$\sigma^2$ вектора столбца и вместе и принимает значения гиперпараметров

  • Возвращает значение предыдущего распределения соединения,, $\pi\left(\beta,\sigma^2\right)$учитывая значения$\beta$ и $\sigma^2$

function logPDF = priorMVTIG(params,ct,st,dof,C,a,b)
%priorMVTIG Log density of multivariate t times inverse gamma 
%   priorMVTIG passes params(1:end-1) to the multivariate t density
%   function with dof degrees of freedom for each component and positive
%   definite correlation matrix C. priorMVTIG returns the log of the product of
%   the two evaluated densities.
%   
%   params: Parameter values at which the densities are evaluated, an
%           m-by-1 numeric vector.
%
%       ct: Multivariate t distribution component centers, an (m-1)-by-1
%           numeric vector.  Elements correspond to the first m-1 elements
%           of params.
%
%       st: Multivariate t distribution component scales, an (m-1)-by-1
%           numeric (m-1)-by-1 numeric vector.  Elements correspond to the
%           first m-1 elements of params.
%
%      dof: Degrees of freedom for the multivariate t distribution, a
%           numeric scalar or (m-1)-by-1 numeric vector. priorMVTIG expands
%           scalars such that dof = dof*ones(m-1,1). Elements of dof
%           correspond to the elements of params(1:end-1).
%
%        C: Correlation matrix for the multivariate t distribution, an
%           (m-1)-by-(m-1) symmetric, positive definite matrix. Rows and
%           columns correspond to the elements of params(1:end-1).
% 
%        a: Inverse gamma shape parameter, a positive numeric scalar.
%
%        b: Inverse gamma scale parameter, a positive scalar.
%
beta = params(1:(end-1));
sigma2 = params(end);

tVal = (beta - ct)./st;
mvtDensity = mvtpdf(tVal,C,dof);
igDensity = sigma2^(-a-1)*exp(-1/(sigma2*b))/(gamma(a)*b^a);

logPDF = log(mvtDensity*igDensity);
end

Создать анонимную функцию, которая работает как priorMVTIG, но принимает только значения параметров и сохраняет значения гиперпараметров, фиксированные в произвольно выбранных значениях.

prednames = ["E" "WR"];
p = numel(prednames);
numcoeff = p + 1;

rng(1); % For reproducibility
dof = 10;
V = rand(numcoeff);
Sigma = 0.5*(V + V') + numcoeff*eye(numcoeff);
st = sqrt(diag(Sigma));
C = diag(1./st)*Sigma*diag(1./st);
ct = rand(numcoeff,1);
a = 10*rand;
b = 10*rand;
logPDF = @(params)priorMVTIG(params,ct,st,dof,C,a,b);

Создайте пользовательскую исходную модель соединения для параметров линейной регрессии. Укажите количество предикторов p. Также укажите дескриптор функции для priorMVTIG и имена переменных.

PriorMdl = bayeslm(p,'ModelType','custom','LogPDF',logPDF,...
    'VarNames',prednames);

PriorMdl является customblm Объект байесовской модели линейной регрессии, представляющий предварительное распределение коэффициентов регрессии и дисперсии возмущений.

Загрузите набор данных Нельсона-Плоссера. Создайте переменные для последовательности ответа и предиктора.

load Data_NelsonPlosser
X = DataTable{:,PriorMdl.VarNames(2:end)};
y = DataTable{:,"GNPR"};

Оцените краевые задние распределения$\beta$$\sigma^2$ гамильтонова образца Монте-Карло (HMC). Укажите 10 000 образцов чертежа и период горения 1000 образцов.

PosteriorMdl = estimate(PriorMdl,X,y,'Sampler','hmc','NumDraws',1e4,...
    'Burnin',1e3);

Method: MCMC sampling with 10000 draws
Number of observations: 62
Number of predictors:   3
 
           |    Mean       Std            CI95         Positive  Distribution 
------------------------------------------------------------------------------
 Intercept |   -3.6486    5.6293  [-16.215,  6.143]      0.246     Empirical  
 E         |   -0.0056    0.0006   [-0.007, -0.004]      0.000     Empirical  
 WR        |   15.2464    0.7727   [13.722, 16.749]      1.000     Empirical  
 Sigma2    | 1287.5830  243.1634  [894.978, 1849.210]    1.000     Empirical

PosteriorMdl является empiricalblm объект модели, хранящий отрисовки из задних распределений.

Просмотрите график трассировки и график ACF рисований из задней части$\beta_1$ (например) и дисперсии возмущений. Не стройте график периода горения.

figure;
subplot(2,1,1)
plot(PosteriorMdl.BetaDraws(2,1001:end));
title(['Trace Plot ' char(8212) ' \beta_1']);
xlabel('MCMC Draw')
ylabel('Simulation Index')
subplot(2,1,2)
autocorr(PosteriorMdl.BetaDraws(2,1001:end))

figure;
subplot(2,1,1)
plot(PosteriorMdl.Sigma2Draws(1001:end));
title(['Trace Plot ' char(8212) ' Disturbance Variance']);
xlabel('MCMC Draw')
ylabel('Simulation Index')
subplot(2,1,2)
autocorr(PosteriorMdl.Sigma2Draws(1001:end))

Образец MCMC дисперсии возмущений, по-видимому, хорошо смешивается.

Открыть сценарий в реальном времени

Рассмотрим регрессионную модель в «Оценочной задней» с использованием гамильтонова образца Монте-Карло. В этом примере используются те же данные и контекст, но вместо этого предполагается диффузная предыдущая модель.

Создайте диффузную предыдущую модель для параметров линейной регрессии. Укажите количество предикторов p и названия коэффициентов регрессии.

p = 3;
PriorMdl = bayeslm(p,'ModelType','diffuse','VarNames',["IPI" "E" "WR"])
PriorMdl = 
  diffuseblm with properties:

    NumPredictors: 3
        Intercept: 1
         VarNames: {4x1 cell}

 
           | Mean  Std        CI95        Positive        Distribution       
-----------------------------------------------------------------------------
 Intercept |  0    Inf  [   NaN,    NaN]    0.500   Proportional to one      
 IPI       |  0    Inf  [   NaN,    NaN]    0.500   Proportional to one      
 E         |  0    Inf  [   NaN,    NaN]    0.500   Proportional to one      
 WR        |  0    Inf  [   NaN,    NaN]    0.500   Proportional to one      
 Sigma2    |  Inf  Inf  [   NaN,    NaN]    1.000   Proportional to 1/Sigma2

PriorMdl является diffuseblm объект модели.

Загрузите набор данных Нельсона-Плоссера. Создайте переменные для последовательности ответа и предиктора.

load Data_NelsonPlosser
X = DataTable{:,PriorMdl.VarNames(2:end)};
y = DataTable{:,'GNPR'};

Оцените условное апостериорное распределение β с учетом данных и того, что start2 = 2, и верните сводную таблицу оценки, чтобы получить доступ к оценкам.

[Mdl,SummaryBeta] = estimate(PriorMdl,X,y,'Sigma2',2);
Method: Analytic posterior distributions
Conditional variable: Sigma2 fixed at   2
Number of observations: 62
Number of predictors:   4
 
           |   Mean      Std          CI95         Positive     Distribution    
--------------------------------------------------------------------------------
 Intercept | -24.2536  1.8696  [-27.918, -20.589]    0.000   N (-24.25, 1.87^2) 
 IPI       |   4.3913  0.0301   [ 4.332,  4.450]     1.000   N (4.39, 0.03^2)   
 E         |   0.0011  0.0001   [ 0.001,  0.001]     1.000   N (0.00, 0.00^2)   
 WR        |   2.4682  0.0743   [ 2.323,  2.614]     1.000   N (2.47, 0.07^2)   
 Sigma2    |    2       0       [ 2.000,  2.000]     1.000   Fixed value

estimate отображает сводку условного заднего распределения β. Ввиду того, что в процессе оценки при 2 фиксируется, выводы о ней тривиальны.

Извлеките средний вектор и ковариационную матрицу условного задника β из сводной таблицы оценки.

condPostMeanBeta = SummaryBeta.Mean(1:(end - 1))
condPostMeanBeta = 4×1

  -24.2536
    4.3913
    0.0011
    2.4682


CondPostCovBeta = SummaryBeta.Covariances(1:(end - 1),1:(end - 1))
CondPostCovBeta = 4×4

    3.4956    0.0350   -0.0001    0.0241
    0.0350    0.0009   -0.0000   -0.0013
   -0.0001   -0.0000    0.0000   -0.0000
    0.0241   -0.0013   -0.0000    0.0055

Показ Mdl. 

Mdl
Mdl = 
  diffuseblm with properties:

    NumPredictors: 3
        Intercept: 1
         VarNames: {4x1 cell}

 
           | Mean  Std        CI95        Positive        Distribution       
-----------------------------------------------------------------------------
 Intercept |  0    Inf  [   NaN,    NaN]    0.500   Proportional to one      
 IPI       |  0    Inf  [   NaN,    NaN]    0.500   Proportional to one      
 E         |  0    Inf  [   NaN,    NaN]    0.500   Proportional to one      
 WR        |  0    Inf  [   NaN,    NaN]    0.500   Proportional to one      
 Sigma2    |  Inf  Inf  [   NaN,    NaN]    1.000   Proportional to 1/Sigma2

Поскольку estimate вычисляет условное апостериорное распределение, оно возвращает исходную предыдущую модель, а не заднюю, в первой позиции списка выходных аргументов.

Оцените условные апостериорные распределения start2, учитывая, что β равно condPostMeanBeta.

[~,SummarySigma2] = estimate(PriorMdl,X,y,'Beta',condPostMeanBeta);
Method: Analytic posterior distributions
Conditional variable: Beta fixed at -24.2536       4.3913   0.00112035      2.46823
Number of observations: 62
Number of predictors:   4
 
           |   Mean      Std          CI95         Positive     Distribution    
--------------------------------------------------------------------------------
 Intercept | -24.2536   0      [-24.254, -24.254]    0.000   Fixed value        
 IPI       |   4.3913   0       [ 4.391,  4.391]     1.000   Fixed value        
 E         |   0.0011   0       [ 0.001,  0.001]     1.000   Fixed value        
 WR        |   2.4682   0       [ 2.468,  2.468]     1.000   Fixed value        
 Sigma2    |  48.5138  9.0088   [33.984, 69.098]     1.000   IG(31.00, 0.00069)

estimate отображает сводку условного апостериорного распределения start2. Потому что β фиксирован к condPostMeanBeta при оценке выводы по ней тривиальны.

Извлеките из сводной таблицы оценки среднее значение и дисперсию условного заднегабаритного значения

condPostMeanSigma2 = SummarySigma2.Mean(end)
condPostMeanSigma2 = 48.5138

CondPostVarSigma2 = SummarySigma2.Covariances(end,end)
CondPostVarSigma2 = 81.1581
Открыть сценарий в реальном времени

Рассмотрим регрессионную модель в «Оценочной задней» с использованием гамильтонова образца Монте-Карло. В этом примере используются те же данные и контекст, но предполагается, что предыдущая модель имеет точку с запятой.

Создайте предшествующую модель с полуконъюгацией для параметров линейной регрессии. Укажите количество предикторов p и названия коэффициентов регрессии.

p = 3;
PriorMdl = bayeslm(p,'ModelType','semiconjugate',...
    'VarNames',["IPI" "E" "WR"]);

PriorMdl является semiconjugateblm объект модели.

Загрузите набор данных Нельсона-Плоссера. Создайте переменные для последовательности ответа и предиктора.

load Data_NelsonPlosser
X = DataTable{:,PriorMdl.VarNames(2:end)};
y = DataTable{:,'GNPR'};

Оцените краевые апостериорные распределения β и start2.

rng(1); % For reproducibility
[PosteriorMdl,Summary] = estimate(PriorMdl,X,y);
Method: Gibbs sampling with 10000 draws
Number of observations: 62
Number of predictors:   4
 
           |   Mean      Std          CI95        Positive  Distribution 
-------------------------------------------------------------------------
 Intercept | -23.9922  9.0520  [-41.734, -6.198]    0.005     Empirical  
 IPI       |   4.3929  0.1458   [ 4.101,  4.678]    1.000     Empirical  
 E         |   0.0011  0.0003   [ 0.000,  0.002]    0.999     Empirical  
 WR        |   2.4711  0.3576   [ 1.762,  3.178]    1.000     Empirical  
 Sigma2    |  46.7474  8.4550   [33.099, 66.126]    1.000     Empirical

PosteriorMdl является empiricalblm объект модели, потому что краевые задние распределения полунъюгатных моделей являются аналитически труднореализуемыми, поэтому estimate должен реализовать пробоотборник Гиббса. Summary - таблица, содержащая оценки и выводы, что estimate отображается в командной строке.

Отображение сводной таблицы.

Summary
Summary=5×6 table
                   Mean          Std                  CI95              Positive    Distribution                                  Covariances                              
                 _________    __________    ________________________    ________    _____________    ______________________________________________________________________

    Intercept      -23.992         9.052       -41.734       -6.1976     0.0053     {'Empirical'}        81.938        0.81622     -0.0025308        0.58928              0
    IPI             4.3929       0.14578        4.1011        4.6782          1     {'Empirical'}       0.81622       0.021252    -7.1663e-06      -0.030939              0
    E            0.0011124    0.00033976    0.00045128     0.0017883     0.9989     {'Empirical'}    -0.0025308    -7.1663e-06     1.1544e-07    -8.4598e-05              0
    WR              2.4711        0.3576        1.7622        3.1781          1     {'Empirical'}       0.58928      -0.030939    -8.4598e-05        0.12788              0
    Sigma2          46.747         8.455        33.099        66.126          1     {'Empirical'}             0              0              0              0         71.487

Доступ к 95% эквивалентному достоверному интервалу коэффициента регрессии IPI.

Summary.CI95(2,:)
ans = 1×2

    4.1011    4.6782

Входные аргументы

свернуть все

Байесовская модель линейной регрессии, представляющая предыдущую модель, заданную в этой таблице как объект.

Объект моделиОписание
conjugateblmЗависимая, нормально-обратно-гамма-сопряженная модель, возвращаемая bayeslm или estimate
semiconjugateblmНезависимая, нормально-обратно-гамма-полунъюгатная модель, возвращаемая bayeslm
diffuseblmДиффузная предыдущая модель, возвращенная bayeslm
empiricalblmПредыдущая модель, характеризующаяся выборками из предыдущих распределений, возвращенная bayeslm или estimate
customblmОбъявленная функция предыдущего распределения, возвращенная bayeslm

PriorMdl может также представлять заднюю модель сустава, возвращаемую estimate, либо conjugateblm или empiricalblm объект модели. В этом случае estimate обновляет апостериорное распределение сустава, используя новые наблюдения в X и y.

Данные предиктора для модели множественной линейной регрессии, указанной как numObservationsоколо-PriorMdl.NumPredictors числовая матрица. numObservations - количество наблюдений и должно быть равно длине y.

Типы данных: double

Данные ответа для модели множественной линейной регрессии, заданной как числовой вектор с numObservations элементы.

Типы данных: double

Аргументы пары «имя-значение»

Укажите дополнительные пары, разделенные запятыми Name,Value аргументы. Name является именем аргумента и Value - соответствующее значение. Name должен отображаться внутри кавычек. Можно указать несколько аргументов пары имен и значений в любом порядке как Name1,Value1,...,NameN,ValueN.

Пример: 'Sigma2',2 определяет оценку условного апостериорного распределения коэффициентов регрессии, заданных данными, и что указанная дисперсия возмущения равна 2.
Опции для всех предыдущих дистрибутивов

свернуть все

Флаг для отображения сводки байесовской оценки в командной строке, указанной как разделенная запятыми пара, состоящая из 'Display' и значение в этой таблице.

СтоимостьОписание
trueestimate печатает информацию оценки и таблицу, суммирующую байесовские оценки, в командной строке.
falseestimate не печатается в командной строке.

Оценочная информация включает в себя способ оценки, фиксированные параметры, количество наблюдений и количество предикторов. Сводная таблица содержит оценочные задние средние и стандартные отклонения (квадратный корень задней дисперсии), 95% равных достоверных интервалов, заднюю вероятность того, что параметр больше 0, и описание заднего распределения (если известно).

Если указан один из Beta или Sigma2, то estimate включает вашу спецификацию в дисплей, и соответствующие задние оценки тривиальны.

Пример: 'Display',false

Типы данных: logical

Опции для всех предыдущих распределений, кроме эмпирических

свернуть все

Значение коэффициентов регрессии для оценки условного апостериорного распределения дисперсии возмущений, определяемое как пара, разделенная запятыми, состоящая из 'Beta' и (PriorMdl.Intercept + PriorMdl.NumPredictors) -по-1 числовой вектор .estimate оценивает характеристики δ (start2 |y,X,β = Beta), где y является y, X является X, и Beta - значение 'Beta'. Если PriorMdl.Intercept является true, то Beta(1) соответствует перехвату модели. Все остальные значения соответствуют переменным предиктора, которые составляют столбцы X. Beta не может содержать никаких NaN значения (то есть все коэффициенты должны быть известны).

Невозможно указать Beta и Sigma2 одновременно.

По умолчанию estimate не вычисляет характеристики условного заднегруди, соответствующего

Пример: 'Beta',1:3

Типы данных: double

Значение дисперсии возмущений для оценки условного апостериорного распределения коэффициентов регрессии, определяемое как пара, разделенная запятыми, состоящая из 'Sigma2' и положительный числовой скаляр. estimate оценивает характеристики δ (β |y,X,Sigma2), где y является y, X является X, и Sigma2 - значение 'Sigma2'.

Невозможно указать Sigma2 и Beta одновременно.

По умолчанию estimate не вычисляет характеристики условной задней части β.

Пример: 'Sigma2',1

Типы данных: double

Параметры для полурегулируемых, эмпирических и пользовательских предыдущих распределений

свернуть все

Моделирование Монте-Карло скорректировало размер выборки, указанный как пара, разделенная запятыми, состоящая из 'NumDraws' и положительное целое число. estimate фактически розыгрыши BurnIn + NumDraws*Thin выборки, но она основывает оценки на NumDraws образцы. Для получения подробной информации о том, как estimate сокращает полную выборку Монте-Карло, см. Алгоритмы.

Если PriorMdl является semiconjugateblm модель и вы указываете Beta или Sigma2, то MATLAB ® игнорируетNumDraws.

Пример: 'NumDraws',1e7

Типы данных: double

Параметры для полуконъюгации и пользовательских предыдущих распределений

свернуть все

Количество вытягиваний, удаляемых из начала выборки Монте-Карло для уменьшения переходных эффектов, указанное как пара, разделенная запятыми, состоящая из 'BurnIn' и неотрицательный скаляр. Для получения подробной информации о том, как estimate сокращает полную выборку Монте-Карло, см. Алгоритмы.

Совет

Чтобы определить подходящий размер периода горения, определите степень переходного поведения в выборке Монте-Карло, указав 'BurnIn',0, моделируя несколько тысяч наблюдений с использованием simulate, а затем построение контуров.

Пример: 'BurnIn',0

Типы данных: double

Скорректированный множитель размера выборки Монте-Карло, указанный как пара, разделенная запятыми, состоящая из 'Thin' и положительное целое число.

Фактический размер выборки Монте-Карло составляет BurnIn + NumDraws*Thin. После выгорания, estimate отбрасывает каждый Thin – 1 рисует, а затем сохраняет следующий. Для получения подробной информации о том, как estimate сокращает полную выборку Монте-Карло, см. Алгоритмы.

Совет

Чтобы уменьшить потенциальную большую последовательную корреляцию в выборке Монте-Карло или уменьшить потребление памяти для розыгрышей, хранящихся в PosteriorMdl, укажите большое значение для Thin.

Пример: 'Thin',5

Типы данных: double

Начальные значения коэффициентов регрессии для выборки Монте-Карло (MCMC) цепи Маркова, указанной как пара, разделенная запятыми, состоящая из 'BetaStart' и вектор числового столбца с (PriorMdl.Intercept + PriorMdl.NumPredictors) элементы. По умолчанию BetaStart - оценка обычных наименьших квадратов (OLS).

Совет

Хорошей практикой является запуск estimate несколько раз с использованием различных начальных значений параметров. Убедитесь, что решения из каждого прогона сходятся к аналогичным значениям.

Пример: 'BetaStart',[1; 2; 3]

Типы данных: double

Начальные значения дисперсии возмущений для выборки MCMC, указанные как пара, разделенная запятыми, состоящая из 'Sigma2Start' и положительный числовой скаляр. По умолчанию Sigma2Start - остаточная среднеквадратическая ошибка ОЛС.

Совет

Хорошей практикой является запуск estimate несколько раз с использованием различных начальных значений параметров. Убедитесь, что решения из каждого прогона сходятся к аналогичным значениям.

Пример: 'Sigma2Start',4

Типы данных: double

Опции для пользовательских предыдущих дистрибутивов

свернуть все

Репараметризация start2 как log (start2) при апостериорной оценке и моделировании, определяемая как разделенная запятыми пара, состоящая из 'Reparameterize' и значение в этой таблице.

СтоимостьОписание
falseestimate не производит репараметризацию,
trueestimate репараметризует start2 как log (start2 ).estimate преобразует результаты обратно в исходный масштаб и не изменяет функциональную форму PriorMdl.LogPDF.

Совет

Если вы испытываете числовые неустойчивости при апостериорной оценке или моделировании start2, то укажите 'Reparameterize',true.

Пример: 'Reparameterize',true

Типы данных: logical

Дискретизатор MCMC, указанный как разделенная запятыми пара, состоящая из 'Sampler' и значение в этой таблице.

СтоимостьОписание
'slice'Пробоотборник срезов
'metropolis'Выборка Random Walk Metropolis
'hmc'Гамильтонианский образец Монте-Карло (HMC)

Совет

  • Чтобы повысить качество розыгрышей MCMC, настройте пробоотборник.

    1. Перед вызовом estimate, укажите параметры настройки и их значения с помощью sampleroptions. Например, чтобы задать ширину образца среза width, использовать:

      options = sampleroptions('Sampler',"slice",'Width',width);

    2. Укажите объект, содержащий спецификации параметров настройки, возвращаемые sampleroptions с помощью 'Options' аргумент пары имя-значение. Например, для использования параметров настройки в options, укажите:

      'Options',options

  • Если указан образец HMC, то рекомендуется задать градиент для некоторых переменных, по крайней мере. estimate прибегает к численному вычислению любых отсутствующих частных производных (NaN значения) в градиентном векторе.

Пример: 'Sampler',"hmc"

Типы данных: string

Параметры пробоотборника, указанные как пара, разделенная запятыми, состоящая из 'Options' и массив структуры, возвращенный sampleroptions. Использовать 'Options' для указания дискретизатора MCMC и его значений параметров настройки.

Пример: 'Options',sampleroptions('Sampler',"hmc")

Типы данных: struct

Типичная ширина интервала выборки вокруг текущего значения в предельных распределениях для дискретизатора среза, указанного как пара, разделенная запятыми, состоящая из 'Width' и положительный числовой скаляр или a (PriorMdl.Intercept + PriorMdl.NumPredictors + 1) -по-1 числовой вектор положительных значений. Первый элемент соответствует перехвату модели, если он существует в модели. СледующееPriorMdl.NumPredictors элементы соответствуют коэффициентам переменных предиктора, упорядоченным столбцами данных предиктора. Последний элемент соответствует отклонению модели.

  • Если Width является скаляром, то estimate применяется Width ко всем PriorMdl.NumPredictors + PriorMdl.Intercept + 1 предельные распределения.

  • Если Width является числовым вектором, то estimate применяет первый элемент к перехвату (если он существует), следующий PriorMdl.NumPredictors элементы к коэффициентам регрессии, соответствующим переменным предиктора в Xи последний элемент дисперсии возмущений.

  • Если размер выборки (size(X,1)) меньше 100, то Width является 10 по умолчанию.

  • Если размер выборки не менее 100, то estimate наборы Width к вектору соответствующих задних стандартных отклонений по умолчанию, предполагая диффузную предшествующую модель (diffuseblm).

Типичная ширина образца среза не влияет на сходимость образца MCMC. Это влияет на количество требуемых оценок функций, то есть на эффективность алгоритма. Если ширина слишком мала, то алгоритм может реализовать избыточное количество оценок функций для определения соответствующей ширины выборки. Если ширина слишком велика, то алгоритму, возможно, придется уменьшить ширину до соответствующего размера, что требует оценки функций.

estimate посылает Width в slicesample функция. Дополнительные сведения см. в разделе slicesample.

Совет

  • Для обеспечения максимальной гибкости задайте ширину образца среза width с помощью 'Options' аргумент пары имя-значение. Например:

    'Options',sampleroptions('Sampler',"slice",'Width',width)

Пример: 'Width',[100*ones(3,1);10]

Выходные аргументы

свернуть все

Байесовская модель линейной регрессии, хранящая характеристики распределения, возвращенные как conjugateblm, semiconjugateblm, diffuseblm, empiricalblm, или customblm объект модели.

  • Если вы не указываете ни Beta или Sigma2 (их значения: []), то estimate обновляет предыдущую модель с использованием вероятности данных для формирования заднего распределения. PosteriorMdl характеризует заднее распределение. Его тип объекта зависит от предшествующего типа модели (PriorMdl).

    Объект моделиPriorMdl
    conjugateblm conjugateblm или diffuseblm
    empiricalblm semiconjugateblm, empiricalblm, или customblm

  • Если указать либо Beta или Sigma2, то PosteriorMdl равняется PriorMdl (две модели являются одним и тем же объектом, в котором хранятся одинаковые значения свойств). estimate не обновляет предыдущую модель для формирования задней модели. Однако estBeta, EstBetaCov, estSigma2, estSigma2Var, и Summary хранить условные апостериорные оценки.

Для получения дополнительной информации об отображении PosteriorMdl, см. Summary.

Дополнительные сведения о поддерживаемых задних распределениях, которые поддаются аналитическому отслеживанию, см. в разделе Аналитически отслеживаемые апостериоры.

Сводка байесовских оценок, возвращенная в виде таблицы. Summary содержит ту же информацию, что и отображение сводки оценки (Display). Строки соответствуют параметрам, а столбцы соответствуют этим задним характеристикам для каждого параметра:

  • Mean - Заднее среднее

  • Std - Заднее стандартное отклонение

  • CI95 - 95% равный достоверный интервал

  • Positive - Задняя вероятность параметра больше 0

  • Distribution - Описание предельного или условного заднего распределения параметра, если оно известно

  • Covariances - Оценочная ковариационная матрица коэффициентов и дисперсии возмущений

Имена строк - это имена в PriorMdl.VarNames. Имя последней строки: Sigma2.

В качестве альтернативы, пройти PosteriorMdl кому summarize для получения сводки байесовских оценок.

Ограничения

Если PriorMdl является empiricalblm объект модели. Невозможно указать Beta или Sigma2. Нельзя оценить условные апостериорные распределения, используя эмпирическое предварительное распределение.

Подробнее

свернуть все

Байесовская модель линейной регрессии

Байесовская модель линейной регрессии рассматривает параметры β и start2 в модели множественной линейной регрессии (MLR) yt = xtβ + αt как случайные величины.

Для времени t = 1,...,T:

  • yt - наблюдаемый ответ.

  • xt - вектор строки 1-by- (p + 1) наблюдаемых значений p предикторов. Чтобы разместить пересечение модели, x1t = 1 для всех t.

  • β - вектор (p + 1) -by-1-столбца коэффициентов регрессии, соответствующих переменным, составляющим столбцы xt.

  • αt - случайное возмущение со средним значением ноля и Cov (λ) = start2IT × T, в то время, как start- T-by-1 вектор, содержащий все возмущения. Эти допущения подразумевают, что вероятность данных

    ℓ (β, start2 | y, x) =∏t=1Tϕ (yt; xtβ, start2).

    (yt; xtβ, start2) - гауссова плотность вероятности со средним значением xtβ и дисперсией start2, оцениваемой при yt;.

Перед рассмотрением данных необходимо наложить совместное предварительное предположение о распределении на (β, start2). В байесовском анализе выполняется обновление распределения параметров с использованием информации о параметрах, полученных из вероятности получения данных. Результатом является совместное апостериорное распределение (β, start2) или условное апостериорное распределение параметров.

Совет

  • Моделирование Монте-Карло подвержено изменению. Если estimate использует моделирование Монте-Карло, тогда оценки и выводы могут различаться при вызове estimate многократно при, казалось бы, эквивалентных условиях. Чтобы воспроизвести результаты оценки, установите начальное число случайного числа с помощью rng перед вызовом estimate.

  • Если estimate выдает ошибку при оценке апостериорного распределения с использованием пользовательской предыдущей модели, затем попробуйте скорректировать начальные значения параметров с помощью BetaStart или Sigma2Startили попробуйте изменить объявленную функцию log previous, а затем восстановить модель. Ошибка может указывать на то, что журнал предыдущего распространения –Inf при заданных исходных значениях.

Алгоритмы

  • Всякий раз, когда предыдущее распределение (PriorMdl) и вероятность данных дают аналитически прослеживаемое апостериорное распределение, estimate оценивает решения закрытой формы для оценщиков Байеса. В противном случае estimate прибегает к моделированию Монте-Карло, чтобы оценить параметры и сделать выводы. Дополнительные сведения см. в разделе Апостериорная оценка и вывод.

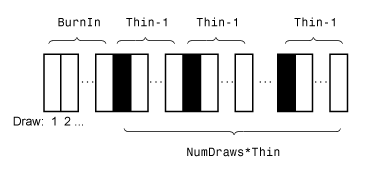
  • На этом рисунке показано, как estimate уменьшает выборку Монте-Карло, используя значения NumDraws, Thin, и BurnIn. Прямоугольники представляют последовательные розыгрыши из распределения. estimate удаляет белые прямоугольники из образца Монте-Карло. Остающееся NumDraws черные прямоугольники составляют образец Монте-Карло.

    Sample reduced by

Вопросы совместимости

развернуть все

Ошибки, начинающиеся с R2019b

См. также

Объекты

Функции

Темы

Представлен в R2017a

Документация по инструментарию Econometrics

Поддержка