Анализ скользящего окна модели временных рядов оценивает:
Стабильность модели с течением времени. Общее предположение модели временного ряда состоит в том, что коэффициенты являются постоянными по отношению ко времени. Проверка нестабильности равносильна проверке того, являются ли коэффициенты инвариантными по времени.
Точность прогноза модели.
Предположим, что в выборке имеются данные для всех периодов. Чтобы проверить стабильность модели временных рядов с помощью скользящего окна, выполните следующие действия.
Выберите размер скользящего окна, m, т.е. количество последовательных наблюдений за скользящим окном. Размер скользящего окна будет зависеть от размера выборки, T и периодичности данных. Как правило, можно использовать короткий размер скользящего окна для данных, собираемых в короткие интервалы, и больший размер для данных, собираемых в более длинные интервалы. Более длинные размеры окна качения имеют тенденцию давать более гладкие оценки окна качения, чем более короткие размеры.
Предположим, что число приращений между последовательными окнами качения равно 1 периоду, затем разбейте весь набор данных на N = T-m + 1 подпробов. Первое скользящее окно содержит наблюдения за период с 1 по m, второе скользящее окно содержит наблюдения за период с 2 по m + 1 и так далее.
Существуют вариации на секциях, например, вместо того, чтобы свернуть одно наблюдение вперед, можно свернуть четыре наблюдения для квартальных данных.
Оцените модель, используя все подкаталоги скользящего окна.
Подготовьте каждую оценку и мудрые пунктом доверительные интервалы (т.е. [SE^ (θ^)]) по катящемуся индексу окна, чтобы видеть, как оценка изменяется со временем. Следует ожидать небольших колебаний для каждого, но большие колебания или тренды указывают на то, что параметр может изменяться во времени.
Дополнительные сведения об оценке стабильности модели с помощью анализа скользящего окна см. в [1].
Предположим, что в выборке имеются данные для всех периодов. Можно выполнить обратную проверку, чтобы проверить прогностическую производительность нескольких моделей временных рядов с помощью скользящего окна. Эти шаги описывают способ обратного тестирования.
Выберите размер скользящего окна, m, т.е. количество последовательных наблюдений за скользящим окном. Размер скользящего окна зависит от размера выборки, T и периодичности данных. Как правило, можно использовать короткий размер скользящего окна для данных, собираемых в короткие интервалы, и больший размер для данных, собираемых в более длинные интервалы. Более длинные размеры окна качения имеют тенденцию давать более гладкие оценки окна качения, чем более короткие размеры.
Выберите горизонт прогноза, h. Горизонт прогноза зависит от применения и периодичности данных. Ниже показано, как скользящее окно секционирует набор данных.
Если число приращений между последовательными окнами качения равно 1 периоду, то весь набор данных разделяется на N = T-m + 1 подпроборов. Первое скользящее окно содержит наблюдения за период с 1 по m, второе скользящее окно содержит наблюдения за период с 2 по m + 1 и так далее. На рисунке показаны разделы.
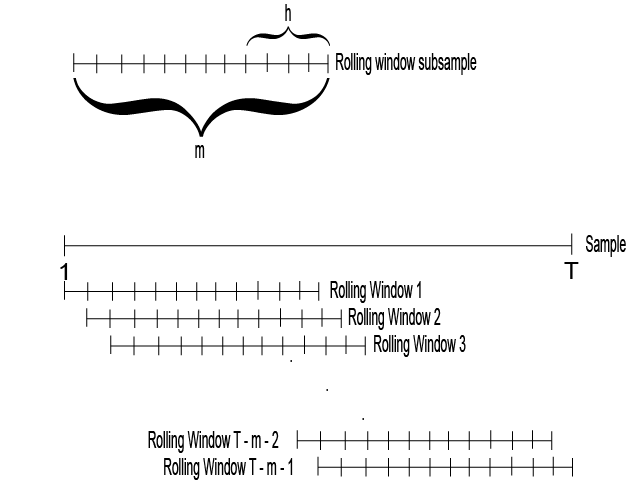
Существуют вариации на секциях, например, вместо того, чтобы свернуть одно наблюдение вперед, можно свернуть четыре наблюдения для квартальных данных.
Для каждого подкаталога скользящего окна:
Оцените каждую модель.
Оценка прогнозов на h-шаг вперед.
Вычислите ошибки прогноза для каждого прогноза, который является , где:
enj - ошибка прогноза катящегося окна n для прогноза j-step-ahead.
y - это ответ.
nj - j-шаговый прогноз скользящего окна, подизмеренного n.
Вычислите корневые среднеквадратические ошибки прогноза (RMSE), используя ошибки прогноза для каждого вида прогноза с опережением шага. Другими словами,
h.
Сравните RMSE между моделями. Модель с самым низким набором RMSE имеет наилучшую прогностическую производительность.
Для получения дополнительной информации о тестировании см. [1].
[1] Zivot, E. и Дж. Ван. Моделирование финансовых временных рядов с помощью S_PLUS®. 2-я редакция NY: Springer Science + Business Media, Inc., 2006.