При построении системы нечеткого вывода, как описано в разделе Процесс нечеткого вывода, можно заменить встроенные функции членства, функции вывода или и то, и другое пользовательскими функциями. В этом разделе вы узнаете, как создать систему нечеткого вывода с помощью пользовательских функций в приложении Fuzzy Logic Designer.
Чтобы создать систему нечеткого вывода с помощью пользовательских функций в приложении Fuzzy Logic Designer:
Откройте конструктор нечеткой логики. В командной строке MATLAB ® введите следующую команду.
fuzzyLogicDesigner
Укажите количество входов и выходов нечеткой системы, как описано в конструкторе нечеткой логики.
Создайте пользовательские функции членства и замените их встроенными функциями членства, как описано в разделе Задание пользовательских функций членства.
Функции членства определяют, как каждая точка во входном пространстве сопоставляется со значением членства от 0 до 1.
Создайте правила с помощью редактора правил, как описано в редакторе правил.
Правила определяют логическую связь между входами и выходами.
Создайте пользовательские функции вывода и замените их встроенными функциями вывода, как описано в разделе Задание пользовательских функций вывода.
Методы вывода включают методы AND, OR, implication, aggregation и defuzzification. Это действие генерирует выходные значения для нечеткой системы.
На следующем рисунке показан пример проблемы, в котором встроенные функции Implication, Aggregation и Defuzzification заменены пользовательскими функциями. customimp, customagg, и customdefuzzсоответственно.
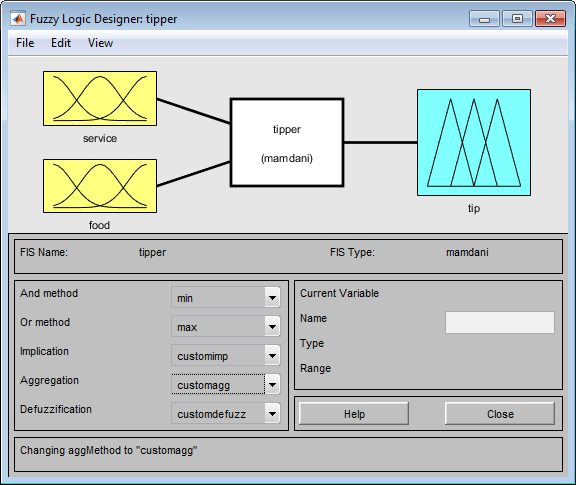
Выберите Вид (View) > Поверхность (Surface), чтобы просмотреть выходные данные системы нечеткого вывода в окне Просмотр поверхностей (Surface Viewer), как описано в разделе Просмотр поверхностей (Surface Viewer).
Можно создать пользовательские функции членства и использовать их в процессе нечеткого вывода. Значения этих функций должны находиться в диапазоне от 0 до 1. Дополнительные сведения о свойствах функций членства см. в разделе Функции членства.
Чтобы создать пользовательскую функцию членства и заменить встроенную функцию членства, выполните следующие действия.
Создайте функцию MATLAB и сохраните ее в текущей рабочей папке.
Сведения о создании функций MATLAB см. в разделе Сценарии и функции.
Следующий код является примером многоступенчатой пользовательской функции членства, custmf1, что зависит от восьми параметров между 0 и 10.
% Function to generate a multi-step custom membership function % using 8 parameters for the input argument x function out = custmf1(x,params) for i = 1:length(x) if x(i) < params(1) y(i) = params(1); elseif x(i) < params(2) y(i) = params(2); elseif x(i) < params(3) y(i) = params(3); elseif x(i) < params(4) y(i) = params(4); elseif x(i) < params(5) y(i) = params(5); elseif x(i) < params(6) y(i) = params(6); elseif x(i) < params(7) y(i) = params(7); elseif x(i) < params(8) y(i) = params(8); else y(i) = 0; end end out = 0.1*y'; % Scale the output to lie between 0 and 1. end
Откройте приложение Fuzzy Logic Designer.
fuzzyLogicDesigner
Конструктор нечеткой логики открывается с именем FIS по умолчанию, Untitled, и содержит один вход, input1 и один выход, output1.
В конструкторе нечеткой логики выберите «Правка» > «Функции членства», чтобы открыть редактор функций членства.
По умолчанию отображаются три функции членства треугольной формы для input1.
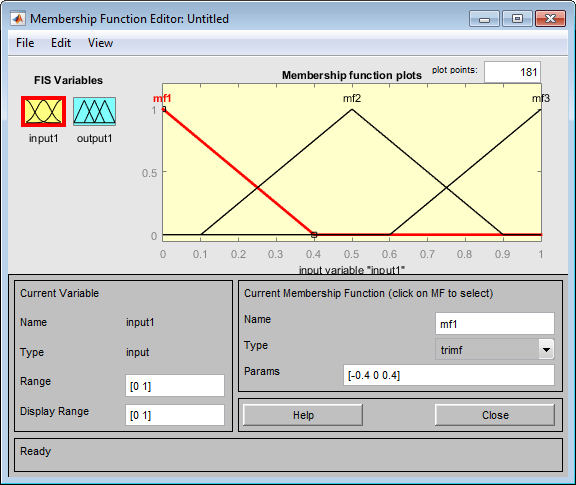
Чтобы заменить функцию членства по умолчанию пользовательской функцией в редакторе функций членства, выполните следующие действия.
Выберите «Правка» > «Удалить все MF», чтобы удалить функции членства по умолчанию для input1.
Выберите меню «Редактирование» > «Добавить пользовательскую ФМ», чтобы открыть диалоговое окно «Пользовательская функция членства».
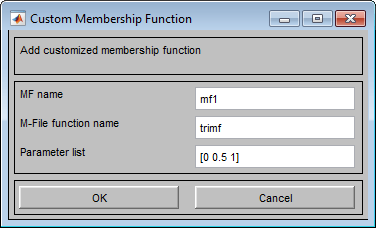
Чтобы задать пользовательскую функцию, в диалоговом окне Пользовательская функция членства выполните следующие действия.
В поле имени MF укажите имя пользовательской функции членства. В этом примере используйте имя customMF1
Примечание
При добавлении дополнительных пользовательских функций членства укажите другое имя MF для каждой функции.
В поле Имя функции M-файла укажите имя файла пользовательской функции членства.
В списке «Параметры» укажите вектор параметров. Для этого примера используйте вектор [0 1 2 4 6 8 9 10].
Эти значения определяют форму и положение функции членства, и функция оценивается с использованием этих значений параметров.
Примечание
Длина вектора параметра должна быть больше или равна числу параметров в пользовательской функции членства.
Использование custmf1 пример на шаге 1, диалоговое окно Custom Membership Function выглядит аналогично следующему рисунку.
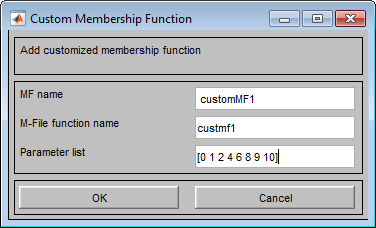
Нажмите кнопку ОК, чтобы добавить пользовательскую функцию членства.
Укажите диапазон и отображаемый диапазон, которые должны быть [0 10] для соответствия диапазону пользовательской функции членства.
Редактор функций членства отображает график пользовательских функций членства.
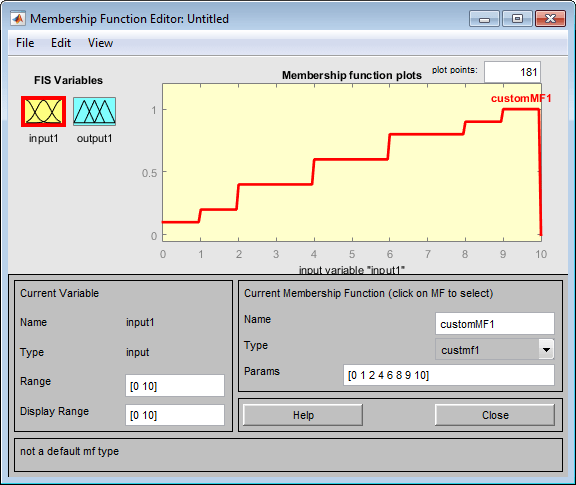
Это действие также добавляет пользовательскую функцию членства в средство просмотра правил и делает ее доступной для создания правил для процесса нечеткого вывода. Чтобы просмотреть пользовательскую функцию в средстве просмотра правил, выберите Править > Правила в конструкторе нечеткой логики или редакторе функций членства.
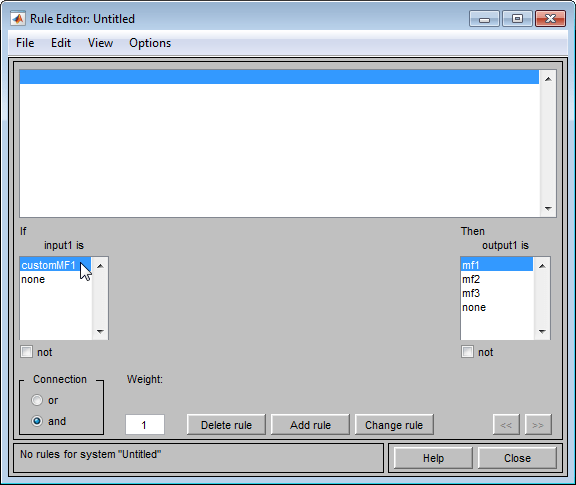
Чтобы добавить пользовательские функции членства для output1, выберите его в редакторе функций членства и повторите шаги 4 и 5.
Можно также добавить пользовательскую функцию членства в FIS в командной строке MATLAB. Например, добавить custmf1 к первой входной переменной, input1 FIS, myFIS, и назовите его customMF1, введите следующее:
myFIS = addMF(myFIS,"input1","custmf1",[0 1 2 4 6 8 9 10],'Name',"customMF1");
Встроенные методы вывода AND, OR, implication, aggregation и defuzzification можно заменить пользовательскими функциями. После создания пользовательской функции вывода сохраните ее в текущей рабочей папке. Сведения о построении нечетких систем с использованием пользовательских функций вывода см. в разделе Создание нечетких систем вывода с использованием пользовательских функций в конструкторе нечеткой логики.
Рекомендации по созданию и заданию функций построения нечетких систем вывода описаны в следующих разделах.
Пользовательские функции вывода AND и OR должны работать на матрице по столбцам аналогично функциям MATLAB. max, min, или prod.
Для вектора строки или столбца x, min(x) возвращает минимальный элемент.
x = [1 2 3 4]; min(x)
ans =
1Для матрицы x, min(x) возвращает вектор строки, содержащий минимальный элемент из каждого столбца.
x = [1 2 3 4;5 6 7 8;9 10 11 12]; min(x)
ans =
1 2 3 4min(x) работает по первому несигнлтонному размеру. Функция min(x,y) возвращает массив того же размера, что и x и y с минимальными элементами от x или y. Любой из входных аргументов может быть скаляром. Функции, такие как max, и prod работают аналогичным образом.
На панели инструментов методы импликации AND выполняют операцию матрицы элемент за элементом, аналогичную функции MATLAB. min(x,y).
a = [1 2; 3 4]; b = [2 2; 2 2]; min(a,b)
ans =
1 2
2 2Методы ИЛИ импликации выполняют операцию матрицы элемент за элементом, аналогичную функции MATLAB max(x,y).
Пользовательские функции импликации должны работать так же, как и функции MATLAB max, min, или prod. Пользовательская функция импликации должна быть операцией нечеткого пересечения T-norm. Дополнительные сведения см. в разделе Дополнительные нечеткие операторы.
Функция импликации должна поддерживать один или два входа, поскольку программное обеспечение вызывает функцию двумя способами:
Чтобы вычислить выходные нечеткие заданные значения, используя интенсивность стрельбы всех правил и соответствующие функции членства на выходе. В этом случае программное обеспечение вызывает функцию импликации, используя два входа, аналогично следующему примеру:
impvals = customimp(w,outputmf)
w - Сила стрельбы нескольких правил, заданная как матрица nr-by-ns. Здесь nr - количество правил, а ns - количество выборок выходных функций членства.
w(:,j) = w(:,1) для всех j. w(i,1) - сила стрельбы i-го правила.
outputmf - выходные значения членских функций, заданные как матрица nr-by-ns. Здесь nr - количество правил, а ns - количество выборок выходных функций членства.
outputmf(i,:) содержит данные i-ой выходной членской функции.
Чтобы вычислить выходное нечеткое значение, используя интенсивность стрельбы одного правила и соответствующую выходную функцию членства для данной выборки. В этом случае программное обеспечение вызывает функцию импликации, используя один вход, аналогично следующему примеру:
impval = customimp([w outputmf])
w и outputmf являются скалярными значениями, представляющими интенсивность стрельбы правила и соответствующее выходное значение функции членства для данной выборки.
Ниже приведен пример ограниченной пользовательской функции импликации произведения с двоичным отображением a + b − 1}. [1]
function y = customimp(x1,x2) if nargin == 1 % x1 assumed to be non-empty column vector or matrix. minVal = zeros(1,size(x1,2)); y = ones(1,size(x1,2)); for i = 1:size(x1,1) y = max(minVal,sum([y;x1(i,:)])-1); end else % x1 and x2 assumed to be non-empty matrices. minVal = zeros(1,size(x1,2)); y = zeros(size(x1)); for i = 1:size(x1,1) y(i,:) = max(minVal,sum([x1(i,:);x2(i,:)])-1); end end end
Примечание
Пользовательские функции импликации не поддерживаются для систем типа Sugeno.
Пользовательские функции агрегации должны работать так же, как и функции MATLAB. max, min, или prod и должны иметь форму y = customagg(x). Пользовательская функция импликации должна быть операцией нечеткого пересечения T-conorm (S-norm). Дополнительные сведения см. в разделе Дополнительные нечеткие операторы.
x - матрица nv-by-nr, представляющая собой список усеченных выходных функций, возвращаемых методом импликации для каждого правила. nv - количество выходных переменных, а nr - число правил. Выходные данные метода агрегирования представляют собой один нечеткий набор для каждой выходной переменной.
Ниже приведен пример пользовательской агрегационной функции с ограниченной суммой с двоичным отображением + b, 1}. [1]
function y = customagg(x) maxVal = ones(1,size(x,2)); y = zeros(1,size(x,2)); for i = 1:size(x,1) y = min(maxVal,sum([y;x(i,:)])); end end
Примечание
Пользовательские функции агрегации не поддерживаются для систем типа Sugeno.
Пользовательские функции дефузификации должны иметь вид y = customdefuzz(x,ymf), где x - вектор значений во входном диапазоне членской функции, и ymf содержит значения функции членства для каждой x значение.
Ниже приведен пример пользовательской функции дефуззификации:
function defuzzfun = customdefuzz(x,ymf) total_area = sum(ymf); defuzzfun = sum(ymf.*x)/total_area; end
Примечание
Пользовательские функции дефузификации не поддерживаются для систем типа Sugeno.
После создания и сохранения пользовательской функции вывода можно указать функцию в системе нечеткого вывода в командной строке или с помощью конструктора нечеткой логики.
Чтобы задать пользовательские функции вывода в конструкторе нечеткой логики, выполните следующие действия.
Примечание
Чтобы задать пользовательскую функцию вывода в Fuzzy Logic Designer, необходимо сначала добавить хотя бы одно правило в FIS.
В левой нижней панели конструктора нечеткой логики выберите Custom из раскрывающегося меню, соответствующего методу вывода, для которого требуется задать пользовательскую функцию.
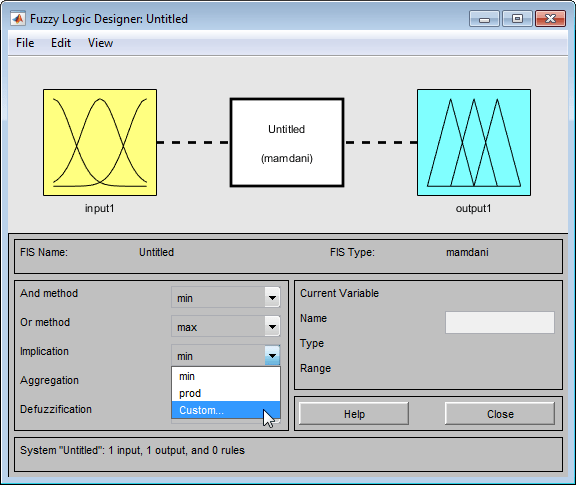
При этом открывается диалоговое окно, в котором указывается имя пользовательской функции вывода.
В поле Имя метода укажите имя пользовательской функции вывода и нажмите кнопку ОК.
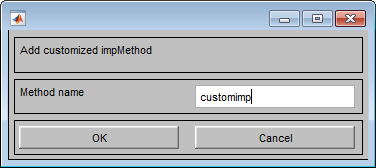
Пользовательская функция заменяет встроенную функцию при построении системы нечеткого вывода.
Чтобы задать пользовательские функции для других методов вывода, повторите шаги 1 и 2.
Задание пользовательских функций вывода для FIS (myFIS) в командной строке MATLAB установите для соответствующего свойства объекта FIS имя функции вывода. Например, чтобы добавить пользовательский элемент, выполните следующие действия.
Метод дефузификации, тип
myFIS.DefuzzificationMethod = "customdefuzz";где customdefuzz - имя пользовательской функции дефуззификации.
Метод импликации, тип
myFIS.ImplicationMethod = "customimp";где customimp - имя пользовательской функции импликации.
Метод агрегирования, тип
myFIS.AggregationMethod = "customagg";где customagg - имя пользовательской функции агрегации.
Для систем нечеткого вывода типа 2 можно задать пользовательскую функцию уменьшения типа. Эта функция должна иметь вид y = customtr(x,umf,lmf), где x - вектор значений во входном диапазоне членской функции. umf и lmf - соответствующие значения верхней и нижней членских функций для каждой x значение. Продукция y - двухэлементный вектор строк центроидов [cL, cR].
Для получения дополнительной информации о сокращении типа посмотрите Тип 2 Fuzzy Inference Systems.
По умолчанию системы Sugeno типа 2 поддерживают только средневзвешенную форму уменьшения типа. Следующая пользовательская функция уменьшения типа реализует форму взвешенной суммы уменьшения типа для системы Sugeno.
function y = customtr(x,umf,ymf) y = zeros(1,2); y(1) = sum(x.*umf); y(2) = sum(x.*lmf); end
Определение пользовательской функции сокращения типа для FIS (myFIS) в командной строке MATLAB, введите
myFIS.DTypeReductionMethod = "customtr";где customtr - имя пользовательской функции дефуззификации.
Пользовательские функции можно использовать в системах нечеткого вывода, для которых создается код. Дополнительные сведения о создании кода для нечетких систем см. в разделе Развертывание нечетких систем вывода.
Если для созданного кода используется тип данных, не содержащий двойных значений, необходимо распространить тип данных из входных аргументов пользовательской функции на выходной аргумент. Например, следующая пользовательская функция агрегации поддерживает тип данных x в y с использованием ones и zeros с 'like' аргумент.
function y = customagg(x) maxVal = ones(1,size(x,2),'like',x); y = zeros(1,size(x,2),'like',x); for i = 1:size(x,1) y = min(maxVal,sum([y;x(i,:)])); end end
Дополнительные сведения о функциях записи, поддерживающих генерацию кода C/C + +, см. в разделе Программирование MATLAB для генерации кода (кодер MATLAB).
[1] Мидзумото, Масахару. «Изобразительные представления нечетких соединений, Часть II: Случаи компенсационных операторов и операторов с двойственными функциями». Нечеткие наборы и системы 32, № 1 (август 1989): 45-79. https://doi.org/10.1016/0165-0114 (89) 90087-0.