Для любого значения во вселенной дискурса традиционная функция членства типа-1 имеет единственное значение членства. Поэтому, хотя функция членства типа 1 моделирует степень членства в данном лингвистическом множестве, она не моделирует неопределенность в степени членства. Для моделирования такой неопределенности можно использовать функции членства типа интервала-2. В таких функциях членства типа 2 степень членства может иметь диапазон значений.
Для примеров, которые используют тип 2 нечеткие системы вывода, посмотрите Нечеткий Контроль за PID с Типом 2 FIS и Предскажите Хаотический Временной ряд Используя Тип 2 FIS.
Функция членства типа 2 интервала определяется верхней и нижней функциями членства. Верхняя функция членства (UMF) эквивалентна традиционной функции членства типа 1. Нижняя функция членства (LMF) меньше или равна верхней функции членства для всех возможных входных значений. Регион между UMF и LMF является следом неопределенности (FOU). На следующей диаграмме показаны UMF (красный), LMF (синий) и FOU (затененный) для треугольной функции членства типа 2.
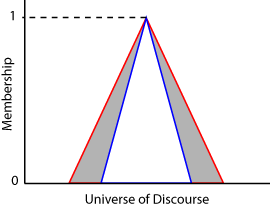
Для каждого входного значения во вселенной дискурса степень принадлежности представляет собой диапазон значений между значениями LMF и UMF.
С помощью программного обеспечения Fuzzy Logic Toolbox™ можно создать системы нечеткого вывода типа 2 Mamdani и Sugeno.
В системах типа-2 Mamdani как входными, так и выходными функциями членства являются нечеткие наборы типа-2.
В системах Sugeno типа 2 только входные функции членства являются нечеткими множествами типа 2. Функции членства на выходе те же, что и для системы Sugeno типа-1 - константа или линейная функция входных значений.
Для создания систем типа-2 Mamdani и Sugeno используйте mamfistype2 и sugfistype2 соответственно. Эти объекты имеют те же параметры, что и тип-1 mamfis и sugfis объекты вместе с дополнительным TypeReductionMethod параметр.
Можно также создать систему нечеткого вывода типа 2 путем преобразования существующей системы типа 1, например, созданной с помощью genfis функция. Для этого используйте convertToType2 функция.
После создания системы нечеткого вывода типа 2 можно:
Оцените нечеткую систему с помощью evalfis функции
Моделирование нечеткой системы с помощью блока контроллера нечеткой логики
Настройте параметры нечеткой системы с помощью tunefis функция
Развертывание нечеткой системы, как описано в разделе Развертывание нечетких систем вывода
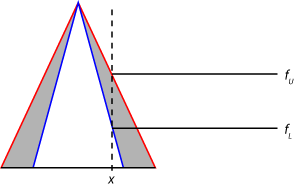
Для систем нечеткого вывода типа 2 входные значения размываются путем нахождения соответствующей степени членства как в UMF, так и в LMF из предшествующего правила. При этом генерируются два нечетких значения для каждой функции членства типа 2. Например, нечеткость на следующем рисунке показывает значение членства в верхней функции членства (fU) и нижней функции членства (fL).
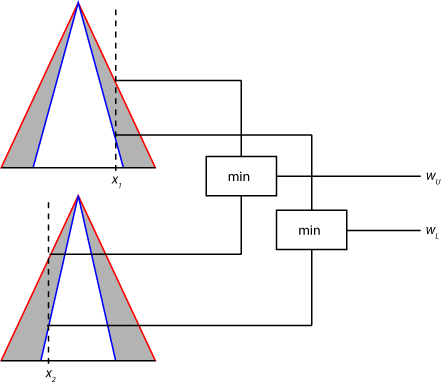
Далее, диапазон уровней возбуждения правила обнаруживается путем применения оператора нечеткости к нечетким значениям функций членства типа-2, как показано на следующем рисунке. Максимальное значение этого диапазона (wU) является результатом применения оператора нечеткости к нечетким значениям из UMF. Минимальное значение (wL) является результатом применения нечеткого оператора к нечетким значениям из LMF
Обработка Antecedent одинакова как для систем Mamdani, так и для систем Sugeno.
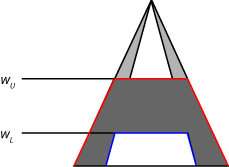
Для системы Mamdani метод импликации клипует (min импликация) или шкалы (prod implication) UMF и LMF функции членства выходного типа-2 с использованием пределов дальности стрельбы правила. Этот процесс создает выходной нечеткий набор для каждого правила. На следующем рисунке показан выходной нечеткий набор (темно-серая область), полученный при применении min отношение к UMF (красный) и LMF (синий).
Для системы Sugeno типа 2 выходной уровень zi для правила i вычисляется таким же образом, как для системы Sugeno типа 1.
Здесь j - входной индекс, xj - значение j-й входной переменной, а c-члены - верхние параметры членской функции.
В отличие от системы Sugeno типа 1, силы срабатывания правила не используются для обработки результата каждого правила. Вместо этого в процессе агрегирования используются уровень вывода и уровни запуска правила.
Цель этапа агрегации состоит в том, чтобы вывести один нечеткий набор типа 2 из выходных нечетких наборов правил.
Для системы Mamdani типа 2 программное обеспечение находит агрегатный нечеткий набор типа 2, применяя метод агрегации к UMF и LMF выходных нечетких наборов всех правил. На следующем рисунке показана агрегация двух нечетких наборов типа 2 (выходные данные для системы с двумя правилами) с использованием max агрегирование.
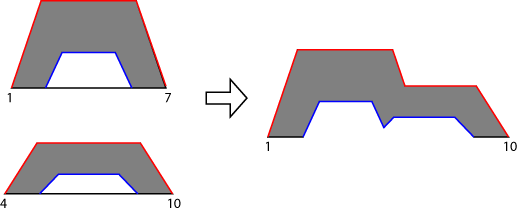
Для системы Sugeno типа 2 агрегатный нечеткий набор получают с помощью следующих шагов:
Сортируйте уровни вывода правила (zi) из всех правил в порядке возрастания. Эти значения выходного уровня определяют вселенную дискурса для нечеткого набора агрегатного типа-2.
Для каждого выходного уровня определите значение UMF, используя максимальное значение диапазона стрельбы из соответствующего правила.
Для каждого выходного уровня определите значение LMF, используя минимальное значение дальности стрельбы из соответствующего правила.
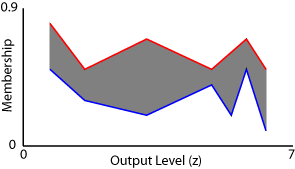
Например, предположим, что у вас есть система Sugeno типа 2 с семью правилами. Кроме того, предположим, что эти правила имеют следующие выходные уровни и пределы дальности стрельбы.
| Правило | Уровень вывода (z) | Минимальное значение обжига | Максимальное значение обжига |
|---|---|---|---|
| 1 | 6.3 | 0.1 | 0.5 |
| 2 | 4.9 | 0.4 | 0.5 |
| 3 | 1.6 | 0.3 | 0.5 |
| 4 | 5.8 | 0.5 | 0.7 |
| 5 | 5.4 | 0.2 | 0.6 |
| 6 | 0.7 | 0.5 | 0.8 |
| 7 | 3.2 | 0.2 | 0.7 |
На следующем рисунке показан агрегированный нечеткий набор типа 2 для этой системы Sugeno с соответствующими UMF (красным) и LMF (синим).
Чтобы найти конечное точное выходное значение для процесса вывода, совокупное нечеткое множество типа-2 сначала сводится к нечеткому множеству типа-1 интервала, которое является диапазоном с нижним пределом cL и верхним пределом cR. Это нечеткое множество типа 1 интервала обычно называют центроидом нечеткого множества типа 2. Теоретически этот центроид является средним значением центроидов всех нечетких множеств типа 1, встроенных в нечеткое множество типа 2. На практике невозможно вычислить точные значения cL и cR. Вместо этого для оценки этих значений используются итеративные методы уменьшения типа.
Для данного нечеткого множества агрегированного типа-2 приблизительные значения cL и cR являются центроидами следующих нечетких множеств типа-1 (зеленые).
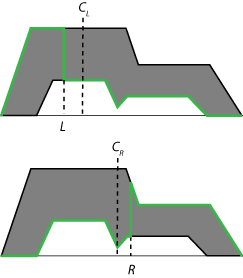
Математически эти центроиды находят с помощью следующих уравнений. [1]
+∑i=R+1Nμumf (xi)
Здесь:
N - количество выборок, взятых в диапазоне выходных переменных, указанных с помощью evalfisOptions.
xi - это i-я выборка выходного значения.
мкумф - верхняя функция членства.
mclmf является более низкой функцией членства.
L и R являются точками переключения, которые оцениваются различными методами уменьшения типа. Список поддерживаемых методов см. в разделе Методы сокращения типов.
Как для систем Mamdani, так и для систем Sugeno конечное значение (y) с дефузифицированным выходом является средним из двух значений центроидов в процессе восстановления типа.
cR2
ПО Fuzzy Logic Toolbox поддерживает четыре встроенных метода сокращения типа. Эти алгоритмы различаются по методам инициализации, допущениям, вычислительной эффективности и условиям завершения.
Чтобы задать метод сокращения типа для нечеткой системы типа 2, установите TypeReduction имущества mamfistype2 или sugfistype2 объект.
| Метод | TypeReduction Значение свойства | Описание |
|---|---|---|
| Карник-Мендель (КМ) [2] | "karnikmendel" | Разработан первый метод снижения типа |
| Усовершенствованный Карник-Мендель (ЭКМ) [3] | "ekm" | Модификация алгоритма Карника-Менделя с улучшенной инициализацией, модифицированным условием окончания и улучшенной вычислительной эффективностью |
| Итеративный алгоритм с условием остановки (МПК) [4] | "iasc" | Итеративное усовершенствование методов грубой силы |
| Усовершенствованный итеративный алгоритм с условием остановки (EIASC) [5] | "eiasc" | Усовершенствованная версия алгоритма МПК |
Как правило, вычислительная эффективность этих методов повышается при перемещении вниз по таблице.
Можно также использовать собственный метод сокращения типа. Дополнительные сведения см. в разделе Создание нечетких систем с использованием пользовательских функций.
[1] Мендель, Джерри М., Хани Хаграс, Вой-Ван Тан, Уильям В. Мелек и Хао Ин. Введение в тип 2 нечеткий логический контроль: теория и приложения. Хобокен, Нью-Джерси: IEEE Press, John Wiley & Sons, 2014.
[2] Карник, Нилеш Н. и Джерри М. Мендель. «Средняя точка нечеткого множества типа 2». Информационные науки 132, № 1-4 (февраль 2001 года): 195-220. https://doi.org/10.1016/S0020-0255 (01) 00069-X.
[3] Ву, Д. и Дж. М. Мендель, «Расширенные алгоритмы Карника-Менделя», IEEE Transactions on Fuzzy Systems, том 17, стр. 923-934. (2009)
[4] Дюран, К., Х. Берналь и М. Мельгарехо, «Усовершенствованный итеративный алгоритм для вычисления обобщенного центроида интервала типа-2 нечеткого набора», Ежегодное собрание Североамериканского общества нечеткой обработки информации, стр. 190-194. (2008)
[5] Wu, D. and M. Nie, «Сравнение и практические реализации алгоритмов снижения типа для нечетких наборов и систем типа 2», Труды FUZZ-IEEE, стр. 2131-2138 (2011)