Нечеткий вывод - это процесс формирования отображения с заданного входа на выход с использованием нечеткой логики. Затем отображение обеспечивает основу, на основе которой могут быть приняты решения или определены закономерности. Процесс нечеткого вывода включает в себя все части, описанные в разделах Функции членства, Логические операции и Правила If-Then.
В этом разделе описывается процесс нечеткого вывода и используется пример задачи с двумя входами, одним выходом и тремя правилами из «Основной проблемы с опрокидыванием». Система нечеткого вывода для этой проблемы принимает обслуживание и качество пищи в качестве входных данных и вычисляет процент чаевых, используя следующие правила.
Если обслуживание плохое или еда прогорклая, то чаевые дешевые.
Если услуга хорошая, то чаевые средние.
Если обслуживание отличное или еда вкусная, то чаевые щедрые.
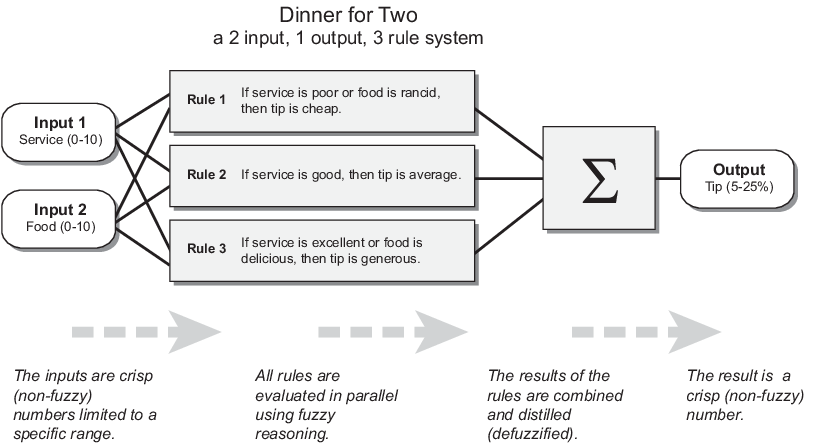
Параллельный характер правил является важным аспектом нечетких логических систем. Вместо резкого переключения между режимами, основанными на точках останова, логика плавно перетекает из регионов, где доминирует то или иное правило.
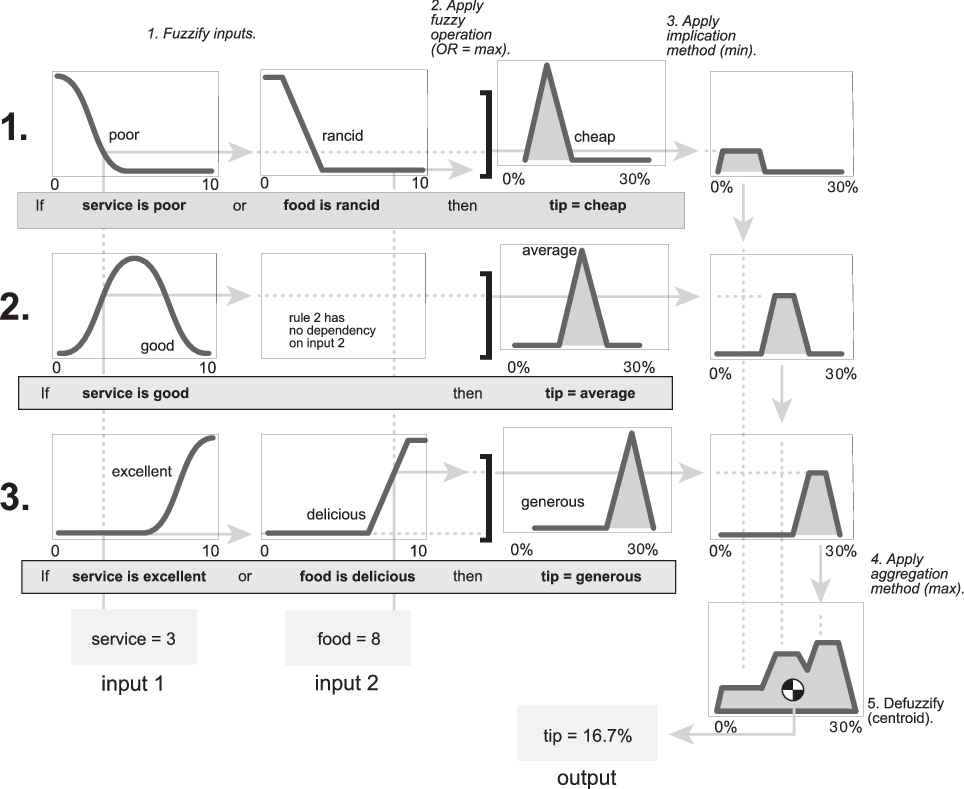
Процесс нечеткого вывода состоит из следующих шагов.
Диаграмма нечеткого вывода отображает все части процесса нечеткого вывода - от нечеткости до дефузификации.
Первым шагом является получение входных данных и определение степени их принадлежности каждому из соответствующих нечетких наборов посредством функций членства (нечеткость). В программном обеспечении Fuzzy Logic Toolbox™ ввод всегда является четким числовым значением, ограниченным вселенной дискурса входной переменной (в этом случае интервал от 0 до 10). Выход представляет собой нечеткую степень членства в квалифицирующем лингвистическом множестве (всегда интервал от 0 до 1). Нечеткость входных данных означает либо поиск в таблице, либо оценку функции.
Этот пример построен на трёх правилах, и каждое из правил зависит от разрешения входов в несколько различных нечетких лингвистических наборов: сервис плохой, сервис хороший, еда прогорклая, еда вкусная и так далее. Прежде чем можно будет оценить правила, входные данные должны быть размыты в соответствии с каждым из этих лингвистических наборов. Например, в какой степени еда вкусная? На следующем рисунке показано, насколько хорошо еда в гипотетическом ресторане (оцененная по шкале от 0 до 10) квалифицируется как лингвистическая переменная вкусная с использованием функции членства. В этом случае мы оцениваем еду как 8, что, учитывая графическое определение вкусного, соответствует («» = 0,7 «») для вкусной функции членства.
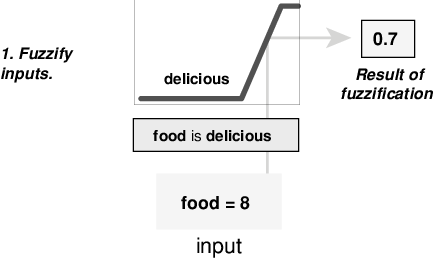
Таким образом, каждый ввод нечетко определяется всеми определяющими функциями членства, требуемыми правилами.
После нечеткости входных данных вы знаете степень, в которой каждая часть предшествующего правила удовлетворяется для каждого правила. Если предшествующий элемент правила имеет более одной части, применяется нечеткий оператор для получения одного числа, представляющего результат предшествующего элемента правила. Это число затем применяется к функции вывода. Входными данными для нечеткого оператора являются два или более значений членства из нечетких входных переменных. Выходные данные представляют собой одно истинное значение.
Как описано в разделе Логические операции, для операции И или операции ИЛИ может использоваться любое количество четко определенных методов. На панели инструментов поддерживаются два встроенных метода AND: min (минимум) и start( продукт). Также поддерживаются два встроенных метода OR: max (максимальный) и probor (вероятностный OR). Вероятностный метод OR (также известный как алгебраическая сумма) вычисляется согласно уравнению:
| пробор (a, b) = a + b - ab |
В дополнение к этим встроенным методам можно создать собственные методы для AND и OR, написав любую функцию и установив ее в качестве выбранного метода. Дополнительные сведения см. в разделе Создание нечетких систем с использованием пользовательских функций.
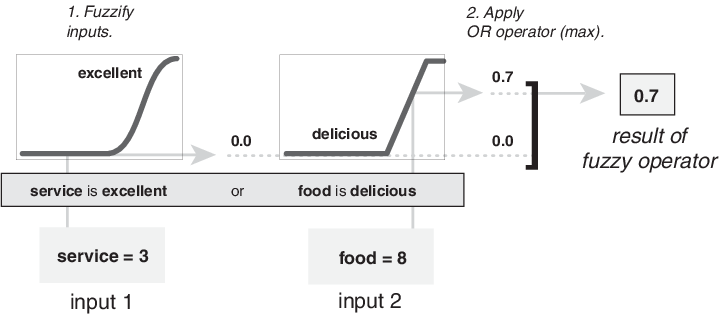
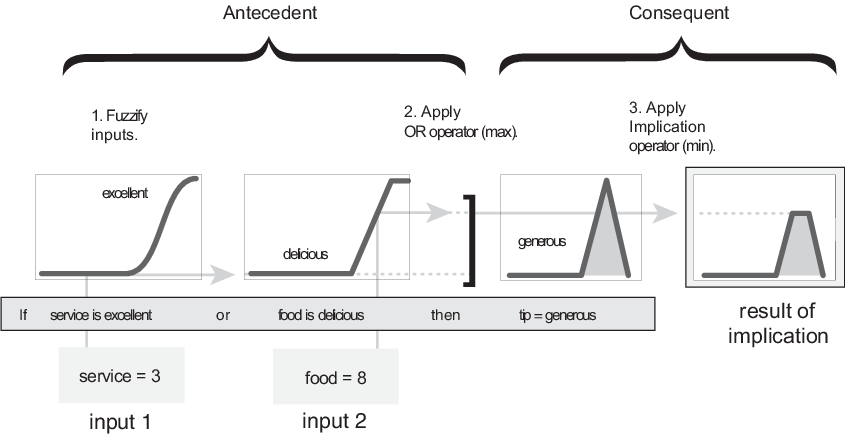
На следующем рисунке показан оператор OR max путем оценки предшествующего значения третьего правила расчета опрокидывания. Для данного рейтинга услуг и продуктов питания два элемента предшествующего периода (сервис отличный, а еда вкусная) производят нечеткие значения членства 0,0 и 0,7 соответственно. Оператор ИЛИ выбирает максимум из двух значений, 0,7. Вероятностный метод ИЛИ все равно приведет к 0,7.
Перед применением метода импликации необходимо определить вес правила. Каждое правило имеет вес (число от 0 до 1), который применяется к числу, заданному предшествующим. Обычно этот вес равен 1 (как и в данном примере) и, таким образом, не оказывает влияния на процесс импликации. Однако можно уменьшить эффект одного правила относительно других, изменив его значение веса на значение, отличное от 1.
После назначения надлежащего взвешивания каждому правилу реализуется метод импликации. Следствием является нечеткое множество, представленное функцией членства, которая соответствующим образом взвешивает приписываемые ей лингвистические характеристики. Последующее изменение формы выполняется с использованием функции, связанной с предшествующим числом (одним числом). Входные данные для процесса импликации представляют собой единственное число, заданное предшествующим числом, а выходные данные представляют собой нечеткое множество. Импликация реализована для каждого правила. Поддерживаются два встроенных метода, и они являются теми же функциями, которые используются методом AND: min (минимум), который усекает выходное нечеткое множество, и start( продукт), который масштабирует выходное нечеткое множество.
Примечание
Системы Sugeno всегда используют метод импликации продукта.
Поскольку решения основываются на проверке всех правил в FIS, выходные данные правил должны быть каким-либо образом объединены. Агрегирование - это процесс, с помощью которого нечеткие наборы, представляющие выходы каждого правила, объединяются в один нечеткий набор. Агрегация выполняется только один раз для каждой выходной переменной, что предшествует заключительному этапу дефузирования. Входные данные процесса агрегации представляют собой список усеченных выходных функций, возвращаемых процессом импликации для каждого правила. Выходные данные процесса агрегирования представляют собой один нечеткий набор для каждой выходной переменной.
Если метод агрегации является коммутативным, то порядок выполнения правил не имеет значения. Поддерживаются три встроенных метода.
max (максимум)
probor (вероятностное ИЛИ)
sum (сумма выходных наборов правил)
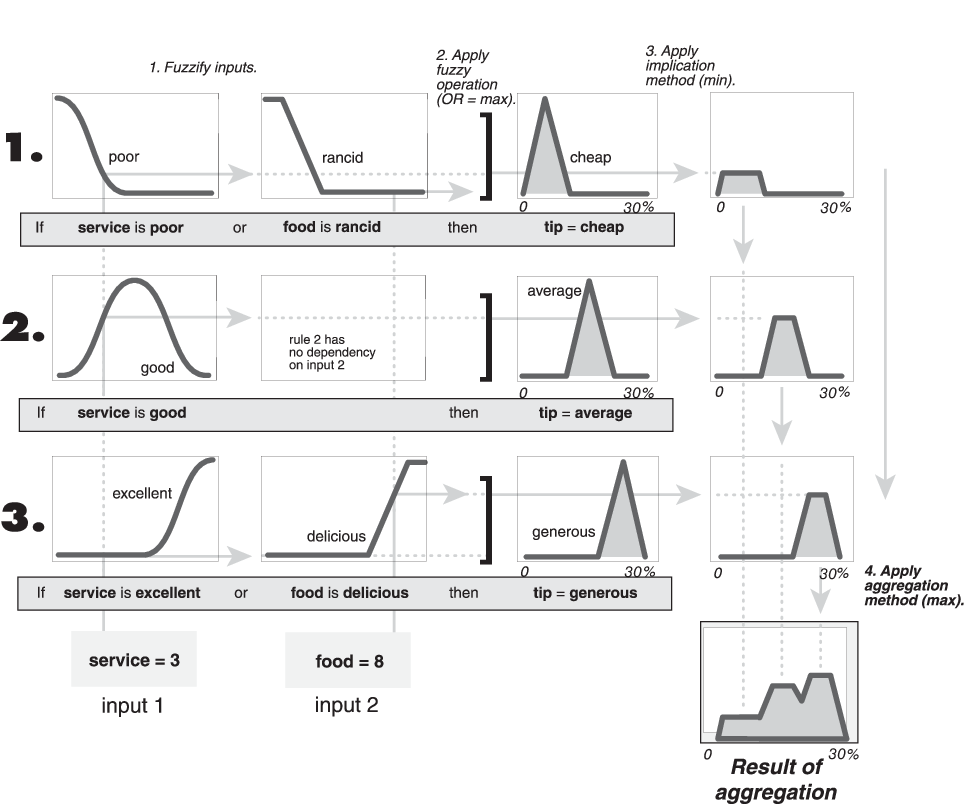
На следующей диаграмме показаны все три правила, чтобы показать, как выходные данные правила агрегируются в один нечеткий набор, функция членства которого назначает взвешивание для каждого выходного значения (кончика).
Примечание
Системы Sugeno всегда используют sum способ агрегации.
Входом для процесса дефузификации является совокупный выходной нечеткий набор, а выходом является одно число. Насколько нечеткость помогает оценке правила во время промежуточных шагов, конечный желаемый выход для каждой переменной обычно является одним числом. Однако агрегат нечеткого набора охватывает диапазон выходных значений и поэтому должен быть дефузифицирован для получения одного выходного значения из набора.
Поддерживаются пять встроенных методов дефузификации: центроид, биссектор, середина максимума (среднее максимальное значение выходного набора), наибольшая из максимумов и наименьшая из максимумов. Возможно, наиболее популярным методом дефузификации является расчет центроида, который возвращает центр области под совокупным нечетким набором, как показано на следующем рисунке.
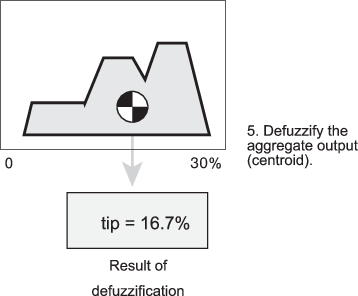
В то время как совокупный выходной нечеткий набор охватывает диапазон от 0% до 30%, значение по умолчанию составляет от 5% до 25%. Эти пределы соответствуют центроидам cheap и generous членские функции соответственно.
Диаграмма нечеткого вывода является составной частью всех меньших диаграмм, представленных до сих пор в этом разделе. Одновременно отображаются все проверенные части процесса нечеткого вывода. Информация проходит через схему нечеткого вывода, как показано на следующем рисунке.
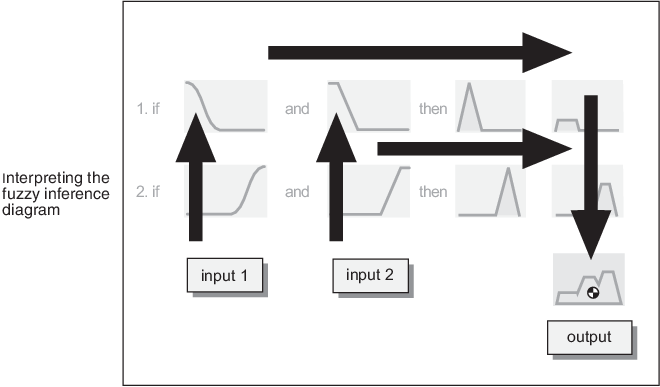
На этом рисунке поток проходит вверх от входов в левом нижнем углу, через каждую строку, а затем вниз от выходов правила к правому нижнему краю. Этот компактный поток показывает все сразу, от нечеткости лингвистических переменных до дефузификации совокупного выхода.
На следующем рисунке показана действительная полноразмерная нечеткая схема вывода для основной проблемы опрокидывания. Используя нечеткую схему вывода, вы можете многое узнать о том, как работает система. Например, для конкретных входных данных на этой диаграмме можно увидеть, что метод импликации является усечением с функцией min. Функция max используется для операции нечеткого ИЛИ. Наиболее сильное влияние на выход оказывает правило 3 (самая нижняя строка на схеме, показанной ранее). Средство просмотра правил, описанное в средстве просмотра правил, представляет собой реализацию нечеткой схемы вывода.