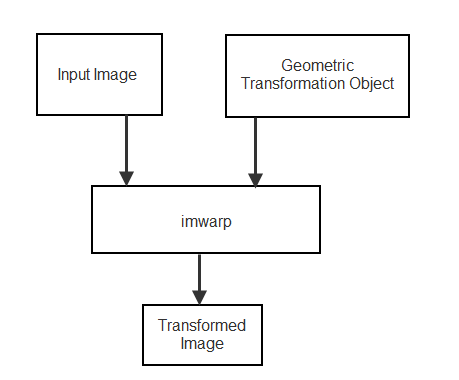
Чтобы выполнить 2-D или 3-D геометрическое преобразование, сначала создайте объект геометрического преобразования, в котором хранится информация о преобразовании. Затем передайте преобразуемое изображение и объект геометрического преобразования в imwarp функция. При необходимости можно предоставить информацию о пространственных ссылках на входное изображение imwarp.
Различные типы объектов геометрического преобразования хранят различную информацию о преобразовании.
rigid2d, affine2d, projective2d, rigid3d, и affine3d объекты хранят матрицу преобразования.
geometricTransform2d и geometricTransform3d объекты сохраняют функцию обратного точечного отображения и, при необходимости, функцию прямого точечного отображения.
Другие типы преобразования, включая LocalWeightedMeanTransformation2D, PiecewiseLinearTransformation2D, и PolynomialTransformation2D сохранить сопоставление между парами управляющих точек.
Существует несколько способов создания объекта геометрического преобразования.
| Подход к созданию объекта преобразования | affine2d | affine3d |
| projective2d |
| Другие объекты преобразования |
|---|---|---|---|---|---|---|
| Определение матрицы преобразования | X | X | X | X | ||
| Определение пользовательской функции точечного отображения | X | |||||
| Оценка преобразования из пар управляющих точек | X | X | X | |||
| Оценка преобразования с использованием оптимизации подобия | X | X | ||||
| Оценка преобразования с использованием фазовой корреляции | X |
Если известна матрица преобразования для геометрического преобразования, которое необходимо выполнить, можно создать rigid2d, affine2d, projective2d, rigid3d, или affine3d непосредственно объект геометрического преобразования. Дополнительные сведения о создании матрицы преобразования см. в разделе Матричное представление геометрических преобразований.
В следующем примере определяется матрица преобразования для преобразования 2-D и создается affine2d объект геометрического преобразования.
xform = [ 1 0 0
0 1 0
40 40 1 ];
tform_translate = affine2d(xform)tform_translate =
affine2d with properties:
T: [3x3 double]
Dimensionality: 2При наличии функции обратного точечного отображения можно определить пользовательский 2-D и 3-D геометрическое преобразование с помощью geometricTransform2d и geometricTransform3d соответственно.
Следующий пример задает функцию обратного отображения, которая принимает и возвращает точки 2-D в упакованном формате (x, y). Затем в примере создается geometricTransform2d пользовательский объект геометрического преобразования.
inversefn = @(c) [c(:,1)+c(:,2),c(:,1).^2]
inversefn =
function_handle with value:
@(c)[c(:,1)+c(:,2),c(:,1).^2]tform = geometricTransform2d(inversefn)
tform =
geometricTransform2d with properties:
InverseFcn: [function_handle]
ForwardFcn: []
Dimensionality: 2Аналогично, в следующем примере создается geometricTransform3d пользовательский объект геометрического преобразования с использованием функции обратного отображения. В примере задается функция обратного отображения, которая принимает и возвращает 3-D точки в упакованном формате (x, y, z).
inversefn = @(c)[c(:,1)+c(:,2),c(:,1)-c(:,2),c(:,3).^2]
inversefn =
function_handle with value:
@(c)[c(:,1)+c(:,2),c(:,1)-c(:,2),c(:,3).^2]tform = geometricTransform3d(inversefn)
tform =
geometricTransform3d with properties:
InverseFcn: [function_handle]
ForwardFcn: []
Dimensionality: 3Можно создать объект геометрического преобразования, передав два набора пар управляющих точек в fitgeotrans функция. fitgeotrans функция автоматически оценивает преобразование из этих точек и возвращает один из объектов геометрического преобразования.
Для различных преобразований требуется различное количество точек. Например, аффинные преобразования требуют трёх неколлинеарных точек в каждом изображении (треугольник), а проективные преобразования требуют четырёх точек (четырёхугольник).
В этом примере два набора управляющих точек передаются в fitgeotrans, который возвращает affine2d объект геометрического преобразования.
movingPoints = [11 11;21 11; 21 21];
fixedPoints = [51 51;61 51;61 61];
tform_cpp = fitgeotrans(movingPoints,fixedPoints,'affine')
tform_cpp =
affine2d with properties:
T: [3x3 double]
Dimensionality: 2Если у вас есть фиксированное изображение и движущееся изображение, которые немного не выровнены, то вы можете использовать imregtform для оценки аффинного геометрического преобразования, которое выравнивает изображения. imregtform оптимизирует средние квадраты или метрику взаимного информационного сходства Маттеса двух изображений, используя регулярный ступенчатый градиентный спуск или эволюционный оптимизатор «один плюс один». Дополнительные сведения см. в разделе Создание оптимизатора и метрики для регистрации изображений на основе интенсивности.
Если у вас есть фиксированное изображение и движущееся изображение, которые сильно не выровнены, то вы можете использовать imregcorr функция для оценки аффинного геометрического преобразования, которое улучшает выравнивание изображения. Результирующее преобразование можно уточнить с помощью оптимизации подобия.
После определения преобразования в объекте геометрического преобразования выполните преобразование с помощью imwarp функция. При вызове функции укажите преобразуемое изображение и объект геометрического преобразования.
imwarp использует геометрическое преобразование для отображения координат на выходном изображении в соответствующие координаты на входном изображении (обратное отображение). Затем, imwarp использует отображение координат для интерполяции значений пикселей во входном изображении и вычисления выходного значения пикселей.
affine2d | affine3d | fitgeotrans | geometricTransform2d | geometricTransform3d | imwarp | projective2d | rigid2d | rigid3d