Число итераций в оптимизации зависит от критериев остановки решателя. Эти критерии включают несколько допусков, которые можно задать. Как правило, допуск является порогом, который при пересечении останавливает итерации решателя.
Установка допусков и других критериев с помощью optimoptions как описано в разделе Настройка и изменение параметров.
Совет
Обычно устанавливаются допуски, такие как OptimalityTolerance и StepTolerance быть намного выше eps, и обычно выше 1e-14. Установка малых допусков не всегда приводит к точным результатам. Вместо этого решатель может не распознать, когда он сошелся, и может продолжить бесполезные итерации. Значение допуска меньше eps эффективно отключает это состояние остановки. Этот совет не применяется к fzero, которая использует значение по умолчанию eps для TolX толерантность.
optimoptions отображает допуски. Например,
options = optimoptions('fmincon');
[options.OptimalityTolerance,options.FunctionTolerance,options.StepTolerance]ans =
1.0e-06 *
1.0000 1.0000 0.0001Допуски по умолчанию также можно найти в разделе опций страницы ссылки на функцию решателя.
StepTolerance - нижняя граница по размеру ступени, означающая норму (xi - xi + 1). Если решатель пытается выполнить шаг, меньший, чемStepTolerance, итерации заканчиваются. StepTolerance обычно используется как относительная граница, означающая, что итерации заканчиваются, когда | (xi - xi + 1) | <StepTolerance* (1 + | xi |) или аналогичная относительная мера. См. раздел Сведения о допусках.
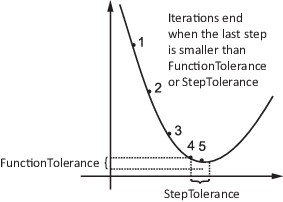
Для некоторых алгоритмов: FunctionTolerance - нижняя граница изменения значения целевой функции во время шага. Для этих алгоритмов, если | f ( xi) - f (xi + 1) | <FunctionTolerance, итерации заканчиваются. FunctionTolerance обычно используется как относительная граница, означающая, что итерации заканчиваются, когда | f ( xi) - f (xi + 1) | <FunctionTolerance* (1 + | f (xi) |) или аналогичная относительная мера. См. раздел Сведения о допусках.
Примечание
В отличие от других решателей, fminsearch останавливается, когда удовлетворяет обоим
TolFun (допуск функции) и TolX (допуск шага).
OptimalityTolerance - допуск для меры оптимальности первого порядка. Если показатель оптимальности меньше OptimalityTolerance, итерации заканчиваются. OptimalityTolerance также может быть относительной границей для меры оптимальности первого порядка. См. раздел Сведения о допусках. Измерение оптимальности первого порядка определено в поле Измерение оптимальности первого порядка.
ConstraintTolerance - верхняя граница по величине любых функций ограничения. Если решатель возвращает точку x с c (x ) >ConstraintTolerance или | ceq (x ) | >ConstraintTolerance, решатель сообщает, что ограничения нарушены при x. ConstraintTolerance также может быть относительной привязкой. См. раздел Сведения о допусках.
Примечание
ConstraintTolerance работает иначе, чем другие допуски. Если ConstraintTolerance не удовлетворяется (т.е. если величина функции ограничения превышает ConstraintTolerance), решатель пытается продолжить, если он не остановлен по другой причине. Решатель не останавливается просто потому, что ConstraintTolerance удовлетворен.
MaxIterations является границей числа итераций решателя. MaxFunctionEvaluations является привязкой к количеству оценок функций. Итерации и оценки функций обсуждаются в разделе Итерации и подсчеты функций.
Существует два других допуска, применимых к конкретным решателям: TolPCG и MaxPCGIter. Они относятся к стадиям предварительно кондиционированного сопряженного градиента. Дополнительные сведения см. в разделе Метод предварительно кондиционированного сопряженного градиента.
Существует несколько допусков, которые применяются только к fmincon алгоритм внутренней точки. Дополнительные сведения см. в разделе Алгоритм внутренних точек в разделе fmincon options.
Существует несколько допусков, которые применяются только к intlinprog. См. раздел Некоторые «целочисленные» решения не являются целыми числами, ветвлением и привязкой.