Ограниченная минимизация - это задача нахождения вектора x, который является локальным минимумом скалярной функции f (x) с учетом ограничений на допустимую x:
)
так, что одно или более из следующих значений имеет: c (x ) ≤ 0, ceq ( x) = 0, A · x ≤ b, Aeq · x = beq , l ≤ x ≤ u. Существует ещё больше ограничений, используемых в полулегком программировании; см. раздел Формулирование и алгоритм проблемы fseminf.
Многие методы, используемые в решателях Optimization Toolbox™, основаны на областях доверия, простой, но мощной концепции оптимизации.
Чтобы понять подход доверительной области к оптимизации, рассмотрим задачу неограниченной минимизации, минимизируйте f (x), где функция принимает векторные аргументы и возвращает скаляры. Предположим, что вы находитесь в точке x в n-пространстве и хотите улучшить, т.е. переместитесь в точку с меньшим значением функции. Основная идея состоит в том, чтобы аппроксимировать f более простой функцией q, которая разумно отражает поведение функции f в окрестности N вокруг точки x. Эта окрестность является областью доверия. Пробный этап s вычисляется путем минимизации (или приблизительно минимизации) над N. Это подпроблема области доверия,
| }. | (1) |
Текущая точка обновляется до x + s, если f ( x + s ) < f (x); в противном случае текущая точка остается неизменной, и N, область доверия, уменьшается, и вычисление пробного этапа повторяется.
Ключевые вопросы при определении конкретного подхода области доверия к минимизации f (x) заключаются в том, как выбрать и вычислить аппроксимацию q (определенную в текущей точке x), как выбрать и изменить область доверия N и как точно решить подпроблему области доверия. В этом разделе рассматривается неограниченная проблема. В последующих разделах обсуждаются дополнительные осложнения из-за наличия ограничений на переменные.
В стандартном способе доверительной области ([48]) квадратичное приближение q определяется первыми двумя членами приближения Тейлора к F при x; окрестность N обычно имеет сферическую или эллипсоидальную форму. Математически обычно указывается подпроблема области доверия
| }, | (2) |
где g - градиент f в текущей точке x, H - гессеновская матрица (симметричная матрица вторых производных), D - диагональная масштабная матрица, Δ - положительный скаляр, а ∥. ∥ - 2-норма. Существуют хорошие алгоритмы для решения уравнения 2 (см. [48]); такие алгоритмы обычно включают вычисление всех собственных значений H и процесс Ньютона, применяемый к светскому уравнению
Такие алгоритмы обеспечивают точное решение уравнения 2. Однако они требуют времени, пропорционального нескольким факторизациям Х. Поэтому для масштабных проблем необходим другой подход. Несколько аппроксимационных и эвристических стратегий, основанных на уравнении 2, были предложены в литературе ([42] и [50]). Подход аппроксимации, используемый в решателях Optimization Toolbox, заключается в ограничении подпроблемы области доверия двумерным подпространством S ([39] и [42]). После вычисления подпространства S работа по решению уравнения 2 является тривиальной, даже если необходима полная информация о собственном значении/собственном векторе (поскольку в подпространстве задача является только двумерной). Доминирующая работа теперь перешла к определению подпространства.
Двумерное подпространство S определяют с помощью процесса предварительно кондиционированного сопряженного градиента, описанного ниже. Решатель определяет S как линейное пространство, охватываемое s1 и s2, где s1 находится в направлении градиента g, а s2 является либо приближенным направлением Ньютона, т.е. решением
| (3) |
или направление отрицательной кривизны,
| (4) |
Философия, лежащая в основе этого выбора S, состоит в том, чтобы форсировать глобальную сходимость (через самое крутое направление спуска или отрицательное направление кривизны) и достичь быстрой локальной сходимости (через шаг Ньютона, когда она существует).
Эскиз неограниченной минимизации с использованием идей области доверия теперь легко дать:
Сформулируйте двухмерную подпроблему области доверия.
Решите уравнение 2, чтобы определить пробный этап s.
Если f (x + s) < f (x), то x = x + s.
Отрегулируйте Δ.
Эти четыре шага повторяются до сходимости. Измерение Δ области доверия корректируется в соответствии со стандартными правилами. В частности, он уменьшается, если стадия испытания не принимается, то есть f (x + s) ≥ f (x). Для обсуждения этого аспекта см. [46] и [49].
Решатели Optimization Toolbox рассматривают несколько важных особых случаев f со специализированными функциями: нелинейные наименьшие квадраты, квадратичные функции и линейные наименьшие квадраты. Однако лежащие в основе алгоритмические идеи те же, что и для общего случая. Эти особые случаи рассматриваются в последующих разделах.
Популярным способом решения больших, симметричных, положительных определённых систем линейных уравнений Hp = -g является метод Предварительно кондиционированных сопряжённых градиентов (PCG). Этот итеративный подход требует возможности вычисления матрично-векторных произведений формы H· v, где v - произвольный вектор. Симметричная положительная определенная матрица М является предварительным условием для Н. То есть М = C2, где C-1HC-1 является хорошо кондиционированной матрицей или матрицей с кластеризованными собственными значениями .
В контексте минимизации можно предположить, что матрица Гессена H симметрична. Однако H гарантированно является положительным определенным только в районе сильного минимизатора. Алгоритм PCG выходит, когда он сталкивается с направлением отрицательной (или нулевой) кривизны, то есть dTHd ≤ 0. Направление р выхода PCG является либо направлением отрицательной кривизны, либо приближенным решением для системы Ньютона Hp = -g. В любом случае p помогает определить двумерное подпространство, используемое в подходе «доверительная область», обсуждаемом в документе «Методы доверительной области для нелинейной минимизации».
Линейные ограничения усложняют ситуацию, описанную для неограниченной минимизации. Однако основные идеи, описанные ранее, могут быть реализованы чистым и эффективным способом. Методы доверительной области в решателях панели инструментов оптимизации генерируют строго выполнимые итерации.
Общая задача минимизации с ограничением линейного равенства может быть записана
| }, | (5) |
где A - матрица m-на-n (m ≤ n). Некоторые решатели Optimization Toolbox предварительно обрабатывают А для удаления строгих линейных зависимостей методом, основанным на факторизации LU AT [46]. Здесь A принимается рангом m.
Метод, используемый для решения уравнения 5, отличается от неограниченного подхода двумя значимыми способами. Сначала вычисляется начальная осуществимая точка x0 с использованием разреженного шага наименьших квадратов, так что Ax0 = b. Во-вторых, алгоритм PCG заменяется на уменьшенные предварительно кондиционированные сопряженные градиенты (RPCG), см. [46], чтобы вычислить приблизительный уменьшенный шаг Ньютона (или направление отрицательной кривизны в нулевом пространстве A). Ключевой шаг линейной алгебры включает в себя решение систем вида
| r0], | (6) |
где аппроксимирует A (малые ненулевые значения A устанавливаются в ноль при условии, что ранг не теряется), а C является разреженным симметричным положительно-определенным приближением к H, т.е. C = H. Подробнее см. [46].
Проблема, связанная с рамкой, имеет вид
| (7) |
где l - вектор нижних границ, а u - вектор верхних границ. Некоторые (или все) компоненты l могут быть равны - ∞, а некоторые (или все) компоненты u могут быть равны ∞. Метод генерирует последовательность строго возможных точек. Два метода используются для поддержания осуществимости при достижении надежного поведения сходимости. Сначала масштабированный измененный шаг Ньютона заменяет неограниченный шаг Ньютона (для определения двумерного подпространства S). Во-вторых, отражения используются для увеличения размера шага.
Масштабированный модифицированный шаг Ньютона возникает при изучении необходимых условий Куна-Такера для уравнения 7,
| g = 0, | (8) |
где
− 1/2),
и вектор v (x) определяется ниже для каждого 1 ≤ i ≤ n:
Если gi < 0 и ui < ∞ то vi = xi - ui
Если gi ≥ 0 и li > - ∞ то vi = xi - li
Если gi < 0 и ui = ∞ то vi = -1
Если gi ≥ 0 и li = - ∞ то vi = 1
Уравнение 8 нелинейной системы не дифференцируется везде. Недифференцируемость возникает, когда vi = 0. Избежать таких моментов можно, сохранив строгую выполнимость, т.е. ограничив l < x < u.
Масштабированный модифицированный шаг Ньютона sk для нелинейной системы уравнений, заданный уравнением 8, определяется как решение линейной системы.
| − g ^ | (9) |
на k-ой итерации, где
| v | 1/2) g, | (10) |
и
| diag (g) Jv. | (11) |
Здесь Сп играет роль якобианца | v |. Каждая диагональная составляющая диагональной матрицы Jv равна 0, -1 или 1. Если все компоненты l и u являются конечными, Jv = diag (знак (g)). В точке, где gi = 0, vi может быть не В такой точке определяется Jiiv = 0. Недифференцируемость этого типа не вызывает беспокойства, поскольку для такого компонента не является существенным, какое значение принимает vi. Кроме того, | vi | все еще будет прерывистым в этой точке, но функция | vi |· gi непрерывна.
Во-вторых, отражения используются для увеличения размера шага. (Один) этап отражения определяется следующим образом. Учитывая шаг p, который пересекает ограничивающее ограничение, рассмотрим первое ограничивающее ограничение, пересекаемое p; предположим, что это ограничение i-ой границы (i-я верхняя или i-я нижняя граница). Затем шаг отражения pR = p, за исключением i-ой составляющей, где pRi = -pi.
При ограниченной оптимизации общая цель состоит в преобразовании проблемы в более простую подпроблему, которая затем может быть решена и использована как основа итеративного процесса. Характеристикой большого класса ранних методов является преобразование ограниченной задачи в основную неограниченную задачу путем использования штрафной функции для ограничений, которые находятся вблизи или за пределами границы ограничения. Таким образом, ограниченная задача решается с помощью последовательности параметризованных неограниченных оптимизаций, которые в пределе (последовательности) сходятся к ограниченной задаче. Эти методы в настоящее время считаются относительно неэффективными и были заменены методами, которые были сосредоточены на решении уравнений Каруша-Куна-Такера (KKT). Уравнения KKT являются необходимыми условиями оптимальности для задачи ограниченной оптимизации. Если задача является так называемой выпуклой задачей программирования, то есть f (x) и Gi (x), i = 1,..., m, являются выпуклыми функциями, то уравнения KKT являются как необходимыми, так и достаточными для глобальной точки решения.
Ссылаясь на GP (уравнение 1), уравнения Куна-Такера могут быть указаны как
| = me + 1,..., m, | (12) |
в дополнение к исходным ограничениям в уравнении 1.
Первое уравнение описывает отмену градиентов между целевой функцией и активными ограничениями в точке решения. Для отмены градиентов необходимы множители Лагранжа (λ i, i = 1,..., m), чтобы сбалансировать отклонения по величине целевой функции и градиентов ограничения. Поскольку в эту операцию отмены включены только активные ограничения, неактивные ограничения не должны включаться в эту операцию, и поэтому для них заданы множители Лагранжа, равные 0. Это косвенно указано в двух последних уравнениях Куна-Такера.
Решение уравнений ККТ составляет основу для многих алгоритмов нелинейного программирования. Эти алгоритмы пытаются вычислить множители Лагранжа напрямую. Ограниченные квазиньютоновские методы гарантируют сверхлинейную сходимость, накапливая информацию второго порядка относительно уравнений KKT, используя процедуру квазиньютоновского обновления. Эти методы обычно называют методами последовательного квадратичного программирования (SQP), поскольку подпроблема QP решается при каждой крупной итерации (также известной как методы итеративного квадратичного программирования, рекурсивного квадратичного программирования и ограниченной переменной метрики).
'active-set' алгоритм не является масштабным; см. Крупномасштабные и среднемасштабные алгоритмы.
Методы SQP представляют собой современные методы нелинейного программирования. Шиттковский [36], например, реализовал и протестировал версию, которая превосходит любой другой проверенный метод по эффективности, точности и проценту успешных решений, по большому количеству проблем тестирования.
Основываясь на работах Биггса [1], Хана [22] и Пауэлла ([32] и [33]), метод позволяет близко имитировать метод Ньютона для ограниченной оптимизации так же, как это делается для неограниченной оптимизации. При каждой большой итерации делается аппроксимация гессена лагранжевой функции методом квази-ньютоновского обновления. Затем используется для генерации подпроблемы QP, решение которой используется для формирования направления поиска для процедуры поиска строки. Обзор SQP найден у Fletcher [13], Gill et al. [19], Пауэлл [35] и Шиттковский [23]. Общий способ, однако, изложен здесь.
Учитывая описание задачи в GP (уравнение 1), основная идея состоит в формулировании подпроблемы QP, основанной на квадратичной аппроксимации лагранжевой функции.
| +∑i=1mλi⋅gi (x). | (13) |
Здесь вы упрощаете уравнение 1, предполагая, что связанные ограничения были выражены как ограничения неравенства. Подпроблему QP можно получить путем линеаризации нелинейных ограничений.
| ≤0, i = me + 1,..., m. | (14) |
Эта подпроблема может быть решена с помощью любого алгоритма QP (см., например, Quadratic Programming Solution). Решение используется для формирования новой итерации
xk + 1 = xk + αkdk.
Параметр α k длины шага определяется соответствующей процедурой поиска строки, так что получается достаточное уменьшение функции качества (см. Обновление матрицы Гессена). Матрица Hk является положительной определённой аппроксимацией гессенской матрицы лагранжевой функции (уравнение 13). Hk может обновляться любым из квазиньютоновских методов, хотя метод BFGS (см. Обновление гессенской матрицы) представляется наиболее популярным.
Нелинейно ограниченная задача часто может быть решена в меньшем количестве итераций, чем неограниченная задача с помощью SQP. Одной из причин этого является то, что из-за ограничений на допустимую область оптимизатор может принимать обоснованные решения относительно направлений поиска и длины шага.
Рассмотрим функцию Розенброка с дополнительным нелинейным ограничением неравенства, g (x),
| (15) |
Это было решено реализацией SQP в 96 итерациях по сравнению со 140 для неограниченного случая. На рис. 5-3, метод SQP для нелинейно ограниченной функции Розенброка показывает путь к точке решения x = [0,9072,0,8228], начиная с x = [-1,9,2,0].
Рис. 5-3, Метод SQP для нелинейно ограниченной функции Розенброка
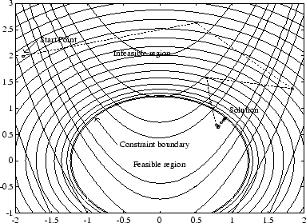
Реализация SQP состоит из трех основных этапов, которые кратко рассматриваются в следующих подразделах:
Обновление Гессенской матрицы. При каждой большой итерации положительное определённое квази-ньютоново приближение гессена лагранжевой функции, H, вычисляется с помощью метода BFGS, где λ i, i = 1,..., m - оценка множителей Лагранжа .
| HkskTHkTskTHksk, | (16) |
где
+∑i=1mλi⋅∇gi (xk)).
Пауэлл [33] рекомендует сохранять гессенский позитив определенным, даже если он может быть положительным неопределенным в точке решения. Поддерживается положительный определенный гессен при условии, что является положительным при каждом обновлении, и что H инициализируется положительной определенной матрицей. Если не является положительным, qk изменяется на поэлементной основе так, что 0. Общая цель этой модификации состоит в том, чтобы как можно меньше искажать элементы qk, которые способствуют позитивному определенному обновлению. Поэтому в начальной фазе модификации самый отрицательный элемент qk * sk многократно уменьшается вдвое. Эта процедура продолжается qkTsk не будет больше или равен малому отрицательному допуску. Если после этой qkTsk все еще не является положительным, измените qk, добавив вектор v, умноженный на постоянный скаляр w, то есть
| wv, | (17) |
где
в противном случае,
и систематически увеличивать w до тех пор, пока не станет положительным.
Функции fmincon, fminimax, fgoalattain, и fseminf все используют SQP. Если Display имеет значение 'iter' в options, то приводятся различные сведения, такие как значения функций и максимальное нарушение ограничения. Когда гессен должен быть изменен с использованием первой фазы предыдущей процедуры, чтобы сохранить его положительным определенным, то Hessian modified отображается. Если гессен должен быть снова модифицирован с использованием второй фазы описанного выше подхода, то Hessian modified twice отображается. Если подпроблема QP неосуществима, то infeasible отображается. Такие дисплеи обычно не вызывают беспокойства, но указывают на то, что проблема в высшей степени нелинейна и что сходимость может занять больше времени, чем обычно. Иногда сообщение no update отображается, указывая, что почти равен нулю. Это может указывать на неправильную настройку проблемы или на то, что вы пытаетесь минимизировать неслагаемую функцию.
Решение для квадратного программирования. При каждой основной итерации метода SQP решается задача QP следующей формы, где Ai ссылается на iтретья строка матрицы А «m-на-n».
| me + 1,..., m. | (18) |
Метод, используемый в функциях Optimization Toolbox, представляет собой стратегию активного набора (также известную как метод проекции), аналогичную стратегии Gill et al., описанной в [18] и [17]. Он был изменен для проблем линейного программирования (LP) и квадратичного программирования (QP).
Процедура решения включает две фазы. Первая фаза включает вычисление возможной точки (если она существует). Вторая фаза включает в себя генерацию итеративной последовательности возможных точек, которые сходятся к решению. В этом способе поддерживается активное множество A _ k, которое является оценкой активных ограничений (то есть тех, которые находятся на границах ограничения) в точке решения. Практически все алгоритмы QP являются методами активного набора. Этот момент подчеркивается, поскольку существует много различных методов, которые очень похожи по структуре, но которые описаны в широко различных терминах.
каждой итерации k обновляется k, и это используется для формирования основы для ^ k поиска. Ограничения равенства всегда остаются в активном A _ k. Обозначение переменной d ^ k используется здесь, чтобы отличить ее от dk в основных итерациях метода SQP. Направление поиска d ^ k вычисляется и минимизирует целевую функцию, оставаясь на любых активных границах ограничения. Возможное подпространство для d ^ k формируется из базиса Zk, столбцы которого ортогональны оценке активного множества (то есть A _ k = 0). Таким образом, направление поиска, которое формируется из линейного суммирования любой комбинации столбцов Zk, гарантированно остается на границах активных ограничений.
Матрица Zk формируется из последних m-1 столбцов QR-разложения матрицы kT, где l - число активных ограничений и l < m То есть Zk задается как
| 1: m], | (19) |
где
R0].
Как только Zk найден, ищут новое направление поиска d ^ k, которое минимизирует q (d), d ^ k находится в нулевом пространстве активных ограничений. То d ^ k является линейной комбинацией столбцов d ^ k = Zkp для некоторого вектора p.
Тогда, если вы рассматриваете квадратичный как функцию p, заменяя d k, вы имеете
| cTZkp. | (20) |
Дифференцирование этого относительно выходов p
| ZkTc. | (21) |
∇q (p) называется спроецированным градиентом квадратичной функции, поскольку он является градиентом, спроецированным в подпространстве, определенном Zk. Термин ZkTHZk называется проектируемым гессенским. Предполагая, что матрица Гессена H является положительной определённой (что и происходит в данной реализации SQP), то минимум функции q (p) в подпространстве, определяемом Zk, возникает, когда ∇q (p ) = 0, что является решением системы линейных уравнений
| ZkTc. | (22) |
Затем выполняется шаг формы.
| ^ k = Zkp. | (23) |
В каждой итерации из-за квадратичной природы целевой функции существует только два выбора длины шага α. Шаг единицы вдоль k является точным шагом к минимуму функции, ограниченной нулевым пространством k. Если такой шаг может быть сделан без нарушения ограничений, то это решение QP ( уравнение 18). В противном случае шаг d ^ k до ближайшего ограничения меньше единицы, и новое ограничение включается в активный набор при следующей итерации. Расстояние до границ ограничения в любом направлении d ^ k задается
| Помощь ^ k}, | (24) |
которая определена для ограничений, не входящих в активный набор, и где направление k направлено к границе ограничения, т.е. 1,..., m.
Когда в активное множество включены n независимых ограничений, без расположения минимума, вычисляются множители Лагранжа λ k, удовлетворяющие неингулярному множеству линейных уравнений
| + Hxk. | (25) |
Если все элементы λ k являются положительными, xk является оптимальным решением QP (уравнение 18). Однако если какая-либо составляющая λ k отрицательна, и составляющая не соответствует ограничению равенства, то соответствующий элемент удаляется из активного множества и ищется новый итерат.
Инициализация. Для запуска алгоритма требуется выполнимая точка. Если текущая точка из метода SQP неосуществима, то можно найти точку, решив задачу линейного программирования
| (26) |
Обозначение Ai указывает i-ю строку матрицы A. Можно найти осуществимую точку (если она существует) уравнения 26, установив значение x, которое удовлетворяет ограничениям равенства. Это значение можно определить, решив недо- или переопределенный набор линейных уравнений, сформированных из набора ограничений равенства. Если есть решение этой задачи, то переменная ослабления γ устанавливается на ограничение максимального неравенства в этой точке.
Можно изменить предшествующий алгоритм QP для задач LP, установив направление поиска на самое крутое направление спуска на каждой итерации, где gk - градиент целевой функции (равный коэффициентам линейной целевой функции).
| ZkZkTgk. | (27) |
Если с помощью предшествующего метода LP найдена приемлемая точка, вводится основная фаза QP. Направление поиска k инициализируется с поиска
| − gk, | (28) |
где gk - градиент целевой функции при текущем итерате xk (т.е. Hxk + c).
Если выполнимое решение не найдено для задачи QP, направление поиска для основной подпрограммы SQP k принимается за направление, которое минимизирует γ.
Функция поиска и оценки строк. Решение подпроблемы QP создает вектор dk, который используется для формирования новой итерации
| + αdk. | (29) |
Параметр α k длины шага определяется для получения достаточного уменьшения функции качества. В этой реализации используется функция качества, используемая Ханом [22] и Пауэллом [33] следующей формы.
| +∑i=me+1mri⋅max[0,gi (x)]. | (30) |
Пауэлл рекомендует установить штрафной параметр
| i = 1,..., m. | (31) |
Это позволяет вносить положительный вклад из ограничений, которые неактивны в решении QP, но недавно были активны. В этой реализации сначала устанавливается штрафной параметр ri
| (x) ‖, | (32) |
где представляет евклидову норму.
Это обеспечивает больший вклад в штрафной параметр от ограничений с меньшими градиентами, что было бы в случае активных ограничений в точке решения.
sqp алгоритм (и почти идентичный sqp-legacy алгоритм) аналогичен active-set (описание см. в разделе Алгоритм активного набора fmincon). Основное sqp алгоритм описан в главе 18 Нокедаля и Райта [31].
sqp алгоритм по существу тот же, что и sqp-legacy алгоритм, но имеет другую реализацию. Обычно, sqp имеет более быстрое время выполнения и меньшее использование памяти, чем sqp-legacy.
Наиболее важные различия между sqp и active-set алгоритмы:
sqp алгоритм выполняет каждый итеративный шаг в области, ограниченной границами. Кроме того, шаги конечных разностей также соответствуют границам. Границы не являются строгими; шаг может быть точно на границе. Эта строгая осуществимость может быть полезной, если целевая функция или функции нелинейных ограничений не определены или являются сложными вне области, ограниченной границами.
Во время итераций sqp алгоритм может попытаться выполнить неудачный шаг. Это означает, что заданная целевая функция или нелинейная функция ограничения возвращает значение Inf, NaNили комплексное значение. В этом случае алгоритм пытается сделать меньший шаг.
sqp алгоритм использует другой набор подпрограмм линейной алгебры для решения подпроблемы квадратичного программирования, уравнение 14. Эти процедуры более эффективны как в использовании памяти, так и в скорости, чем active-set процедуры.
sqp алгоритм имеет два новых подхода к решению уравнения 14, когда ограничения не удовлетворяются.
sqp алгоритм объединяет функции цели и ограничения в функцию качества. Алгоритм пытается минимизировать функцию качества, подверженную ослабленным ограничениям. Эта измененная проблема может привести к выполнимому решению. Однако этот подход имеет больше переменных, чем исходная задача, поэтому размер задачи в уравнении 14 увеличивается. Увеличенный размер может замедлить решение подпроблемы. Эти процедуры основаны на статьях Spellucci [60] и Tone [61]. sqp алгоритм устанавливает штрафной параметр для функции качества Уравнение 30 согласно предложению в [41].
Предположим, что нелинейные ограничения не выполняются, и попытка выполнения шага приводит к росту нарушения ограничения. sqp алгоритм пытается получить осуществимость, используя аппроксимацию второго порядка к ограничениям. Метод второго порядка может привести к выполнимому решению. Однако этот метод может замедлить решение, требуя больше оценок нелинейных функций ограничения.
Подход внутренней точки к ограниченной минимизации заключается в решении последовательности приближенных задач минимизации. Исходная проблема:
| x) ≤0. | (33) |
| и g (x) + s = 0. | (34) |
Приблизительная задача Уравнение 34 представляет собой последовательность задач, ограниченных равенством. Их легче решить, чем исходную проблему 33, ограниченную неравенством.
Для решения приблизительной задачи алгоритм использует один из двух основных типов шагов на каждой итерации:
Прямой шаг в (x, s). На этом этапе пытаются решить уравнения KKT, уравнение 2 и уравнение 3, для аппроксимационной задачи посредством линейной аппроксимации. Это также называется шагом Ньютона.
Стадия CG (сопряженный градиент) с использованием доверительной области.
По умолчанию алгоритм сначала пытается сделать прямой шаг. Если это невозможно, выполняется попытка выполнения шага CG. Один случай, когда он не делает прямого шага, это когда приблизительная задача не является локально выпуклой вблизи текущего итерата.
При каждой итерации алгоритм уменьшает функцию качества, такую как
| (x) + s) ‖. | (35) |
Если целевая функция или нелинейная функция ограничения возвращает комплексное значение NaN, Inf или ошибку при итерации xj, алгоритм отклоняет xj. Отклонение имеет тот же эффект, как если бы функция заслуг не уменьшилась в достаточной степени: алгоритм затем пытается другой, более короткий шаг. Переносить любой код, который может привести к ошибке в try-catch:
function val = userFcn(x)
try
val = ... % code that can error
catch
val = NaN;
endЦель и ограничения должны быть правильными (double) значения в начальной точке.
При определении прямого шага используются следующие переменные:
H обозначает гессен лагранжиана из fstart:
| (x). | (36) |
Jg обозначает якобиан функции ограничения g.
Jh обозначает якобиан функции ограничения h.
S = диаг (ы).
λ обозначает вектор-умножитель Лагранжа, связанный с ограничениями g
Λ = диаг (λ).
y обозначает вектор множителя Лагранжа, связанный с h.
e обозначает вектор единиц того же размера, что и g.
Уравнение 38 определяет прямой шаг (Δx, Δs):
| ]. | (37) |
Это уравнение является прямым результатом попытки решения уравнений 2 и 3 с использованием линеаризованного лагранжиана.
Можно симметрировать уравнение, предварительно умножив вторую переменную Δs на S-1:
| ]. | (38) |
Чтобы решить это уравнение для (Δx, Δs), алгоритм делает факторизацию LDL матрицы. (См. пример 3 - Структура D в MATLAB
®ldl страница ссылки на функцию.) Это самый дорогостоящий в вычислительном отношении шаг. Одним из результатов этой факторизации является определение того, является ли прогнозируемый гессен положительным определенным или нет; если нет, алгоритм использует шаг сопряженного градиента, описанный в шаге сопряженного градиента.
Чтобы приблизительная задача уравнение 34 приблизилась к исходной задаче, барьерный параметр λ должен уменьшаться до 0 по мере выполнения итераций. Алгоритм имеет две опции обновления параметров барьера, которые вы выбираете с помощью BarrierParamUpdate вариант: 'monotone' (по умолчанию) и 'predictor-corrector'.
'monotone' опция уменьшает параметр λ на коэффициент 1/100 или 1/5 всякий раз, когда приближенная задача решается достаточно точно в предыдущей итерации. Он выбирает 1/100, когда алгоритм принимает только одну или две итерации для достижения достаточной точности, и 1/5 в противном случае. Мерой точности является следующий тест, который заключается в том, что размеры всех членов правой части уравнения 38 меньше, чем λ:
h ‖, ‖ c (x) + s ‖) < λ.
Примечание
fmincon переопределяет ваш BarrierParamUpdate выбор для 'monotone' при любом из следующих удержаний:
Проблема не имеет ограничений неравенства, включая связанные ограничения.
SubproblemAlgorithm опция - 'cg'.
В оставшейся части этого раздела обсуждается 'predictor-corrector' алгоритм обновления барьерного параметра Механизм аналогичен алгоритму линейного программирования Predictor-Corrector.
Шаги предиктора-корректора могут ускорить существующий подход Фиакко-Маккормака (Монотон), скорректировав ошибку линеаризации в шагах Ньютона. Эффекты режима Предиктора-Корректора двояки: он (часто) улучшает направления шагов и одновременно адаптивно обновляет барьерный параметр с параметром центрирования, чтобы побудить итератов следовать по «центральному пути». Линейные программы см. в разделе Nocedal and Wright, посвященном шагам предиктора-корректора, чтобы понять, почему центральный путь позволяет увеличить размеры шага и, следовательно, ускорить сходимость.
На шаге предиктора используется линеаризованный шаг с λ = 0, означающий без барьерной функции:
].
Определите ɑs и ɑλ как наибольшие размеры шагов, которые не нарушают ограничения по неотрицательности.
: λ+αΔλ≥0).
Теперь вычислите комплементарность из шага предсказателя.
| αλ Δλ) m, | (39) |
где m - число ограничений.
Первый шаг корректора корректируется для квадратичного члена, забытого в линеаризации поиска корня Ньютона
0+ΔsΔλ︸Quadratic.
Чтобы исправить квадратичную ошибку, решите линейную систему для направления шага корректора.
0ΔsΔλ 00].
Второй этап корректора является этапом центрирования. Коррекция центрирования основана на переменном λ в правой части уравнения
].
В данном случае λ определяется как
3,
где мкР определяется в уравнении 39, и sTλ/m.
Чтобы не допустить слишком быстрого уменьшения барьерного параметра, потенциально дестабилизируя алгоритм, алгоритм сохраняет центрирующий параметр, который превышает 1/100. Это приводит к уменьшению барьерного параметра λ не более чем в 1/100 раз.
Алгоритмически первые шаги коррекции и центрирования независимы друг от друга, поэтому они вычисляются вместе. Кроме того, матрица слева для предиктора и обоих шагов корректора одинакова. Так, алгоритмически матрица факторизируется один раз, и эта факторизация используется для всех этих шагов.
Алгоритм может отклонить предложенный шаг предиктора-корректора, поскольку шаг увеличивает значение функции качества уравнение 35, комплементарность, по меньшей мере, в два раза или вычисленная инерция неверна (проблема выглядит неконвексной). В этих случаях алгоритм пытается сделать другой шаг или сопряженный шаг градиента.
Подход сопряженного градиента к решению приближенной задачи уравнение 34 аналогично другим вычислениям сопряженного градиента. В этом случае алгоритм корректирует как x, так и s, сохраняя s положительными. Подход заключается в минимизации квадратичного приближения к приближенной задаче в доверительной области, подверженной линеаризованным ограничениям.
В частности, пусть R обозначает радиус доверительной области, и пусть другие переменные определяются как в прямом шаге. Алгоритм получает множители Лагранжа, приблизительно решая уравнения KKT
x) = 0,
в смысле наименьших квадратов при условии, что λ является положительным. Затем он делает шаг (Δx, Δs), чтобы приблизительно решить
| (40) |
| + JhΔx = 0. | (41) |
Вот значения и эффекты нескольких вариантов в алгоритме внутренних точек.
HonorBounds - При установке в значение trueкаждый итерат удовлетворяет заданным ограничениям границ. Если установлено значение false, алгоритм может нарушать границы во время промежуточных итераций.
HessianApproximation - Если установлено значение:
'bfgs', fmincon вычисляет гессен по плотному квази-ньютоновскому приближению.
'lbfgs', fmincon вычисляет гессен по ограниченно-запоминающему масштабному квази-ньютоновскому приближению.
'fin-diff-grads', fmincon вычисляет гессеново-кратное векторное произведение посредством конечных разностей градиента (градиентов); другие опции должны быть установлены соответствующим образом.
HessianFcn — fmincon использует дескриптор функции, указанный в HessianFcn для вычисления гессенского. Смотрите «Включая гессенов.»
HessianMultiplyFcn - Дать отдельную функцию для гессенского времени-векторной оценки. Дополнительные сведения см. в разделе Включение гессенских и гессенских функций умножения.
SubproblemAlgorithm - определяет, следует ли пытаться выполнить прямой шаг Ньютона. Настройка по умолчанию 'factorization' позволяет попытаться выполнить этот тип шага. Настройка 'cg' допускает только сопряженные градиентные шаги.
Полный список параметров см. в разделе Алгоритм внутренних точек в fmincon options.
fminbnd - решатель, доступный в любой установке MATLAB. Он решает для локального минимума в одном измерении в пределах ограниченного интервала. Он не основан на производных. Вместо этого он использует поиск золотого сечения и параболическую интерполяцию.
fseminf решает проблемы оптимизации с дополнительными типами ограничений по сравнению с теми, которые решаются fmincon. Формулировка fmincon является
)
так, что c (x ) ≤ 0, ceq ( x) = 0, A · x ≤ b, Aeq · x = beq и l ≤ x ≤ u.
fseminf добавляет следующий набор полулегких ограничений к уже заданным. Для wj в одно- или двумерном ограниченном интервале или прямоугольнике Ij для вектора непрерывных функций K (x, w) ограничения равны
Kj (x, wj ) ≤ 0 для всех wj∈Ij.
Термин «измерение» fseminf задача означает максимальную размерность набора ограничений I: 1, если все Ij являются интервалами, и 2, если хотя бы один Ij является прямоугольником. Размер вектора K не входит в это понятие размерности.
Причина, по которой это называется полулегким программированием, заключается в том, что существует конечное число переменных (x и wj), но бесконечное число ограничений. Это потому, что ограничения на x находятся над набором непрерывных интервалов или прямоугольников Ij, который содержит бесконечное число точек, поэтому существует бесконечное число ограничений: Kj (x, wj ) ≤ 0 для бесконечного числа точек wj .
Можно подумать, что проблему с бесконечным числом ограничений решить невозможно. fseminf решает эту проблему, переформулировав проблему до эквивалентной, которая имеет два этапа: максимизация и минимизация. Полубесконечные ограничения переформулированы как
| , | K |, | (42) |
где | K | - число компонентов вектора K; то есть число полубесконечных функций ограничения. Для фиксированных x это обычная максимизация по ограниченным интервалам или прямоугольникам.
fseminf дополнительно упрощает задачу, делая кусочно-квадратичные или кубические аппроксимации (x, wj) к функциям Kj ( x, wj), для каждого x, которые посещает решатель.fseminf в уравнении 42 рассматривает только максимумы интерполяционной функции (x, wj) вместо Kj (x, wj). Это сводит исходную задачу, минимизируя полубесконечно ограниченную функцию, к задаче с конечным числом ограничений.
Точки отбора проб. Полубесконечная функция ограничения должна предоставлять набор точек выборки, точек, используемых при создании квадратичных или кубических аппроксимаций. Для этого он должен содержать:
Начальный интервал s между точками отбора проб w
Способ генерации набора точек выборки w из s
Начальный интервал s является матрицей | K | -by-2. J-й ряд s представляет интервал для соседних точек выборки для функции ограничения Kj. Если Kj зависит от одномерного wj, set s(j,2) = 0. fseminf обновляет матрицу s в последующих итерациях.
fseminf использует матрицу s для генерации точек выборки w, которые затем используются для создания аппроксимации (x, wj). Процедура создания w изs должен сохранять одинаковые интервалы или прямоугольники Ij во время оптимизации.
Пример создания точек выборки. Рассмотрим проблему с двумя полулегкими ограничениями, K1 и K2. K1 имеет одномерную w1, а K2 - двумерную w2. Следующий код генерирует набор выборок от w1 = 2 до 12:
% Initial sampling interval
if isnan(s(1,1))
s(1,1) = .2;
s(1,2) = 0;
end
% Sampling set
w1 = 2:s(1,1):12;fseminf определяет s как NaN при первом вызове функции ограничения. Проверка этого позволяет установить начальный интервал выборки.
Следующий код генерирует набор выборок из w2 в квадрате, причем каждый компонент проходит от 1 до 100, первоначально дискретизированный чаще в первом компоненте, чем во втором:
% Initial sampling interval if isnan(s(1,1)) s(2,1) = 0.2; s(2,2) = 0.5; end % Sampling set w2x = 1:s(2,1):100; w2y = 1:s(2,2):100; [wx,wy] = meshgrid(w2x,w2y);
Предыдущие фрагменты кода можно упростить следующим образом:
% Initial sampling interval
if isnan(s(1,1))
s = [0.2 0;0.2 0.5];
end
% Sampling set
w1 = 2:s(1,1):12;
w2x = 1:s(2,1):100;
w2y = 1:s(2,2):100;
[wx,wy] = meshgrid(w2x,w2y);fseminf по существу сводит проблему полулегкого программирования к проблеме, решаемой fmincon. fseminf выполняет следующие шаги для решения задач полулегкого программирования:
При текущем значении x, fseminf идентифицирует все wj, i так, что интерполяция (x, wj, i) является локальным максимумом. (Максимальное значение относится к переменному значению w для фиксированного x.)
fseminf делает один итерационный шаг в решении fmincon проблема:
)
так, что c (x ) ≤ 0, ceq ( x) = 0, A · x ≤ b, Aeq · x = beq, и l ≤ x ≤ u, где c (x) дополняется всеми максимумами ( x, wj), взятыми над всеми wj∈Ij, что равно максимумам над j и i ( x, wj, i).
fseminf проверяет, выполняется ли какой-либо критерий остановки в новой точке x (для остановки итераций); если нет, то он продолжает выполнение шага 4.
fseminf проверяет, требуется ли обновление дискретизации полусредненных ограничений, и соответствующим образом обновляет точки выборки. Это обеспечивает обновленную аппроксимацию (x, wj). Затем она продолжается на шаге 1.