Нелинейные особенности обеспечивают метрики, характеризующие хаотичное поведение в сигналах вибрации. Эти характеристики могут быть полезны при анализе вибрационных и акустических сигналов от таких систем, как подшипники, шестерни и двигатели. Создание нелинейных функций требует больших вычислительных затрат, чем создание любых других функций в приложении.
Уникальное преимущество нелинейных элементов заключается в том, что они отражают изменения в траектории фазового пространства базовой динамики системы. Эти изменения могут иметь место даже до возникновения состояния отказа. Таким образом, контроль динамических характеристик системы с использованием нелинейных характеристик может помочь выявить потенциальные неисправности ранее, например, когда подшипник слегка изношен.
Все нелинейные элементы основаны на реконструкции фазового пространства. Фазовое пространство - это многомерное отображение всех возможных переменных состояний. Это сопоставление дает портрет полностью динамического поведения системы. Фазово-пространственная реконструкция - техника, воссоздающая многомерное фазовое пространство из одного одномерного сигнала.
Вложение размерности - размерность фазового пространства, эквивалентная количеству переменных состояния в динамической системе
Lag - значение задержки, используемое для выполнения реконструкции
Дефолт ‘Auto’ задание результатов оценки этих параметров. Изменение параметров вручную для изучения влияния настроек на эффективность результирующих элементов.
Дополнительные сведения о фазовой реконструкции пространства см. в разделе phaseSpaceReconstruction.
Приблизительная энтропия измеряет регулярность сигнала или, наоборот, непредсказуемость сигнала. Деградация в системе обычно увеличивает приблизительную энтропию.
Радиус - критерий подобия, определяющий значимый диапазон, в котором колебания данных должны считаться аналогичными. ‘Auto’ установка вызывает значение по умолчанию, которое основано на дисперсии или ковариации сигнала.
Корреляционная размерность измеряет сложность хаотического сигнала, что отражает самоподобие. Ухудшение обычно увеличивает сложность сигнала и при этом увеличивает значение этой метрики.
Радиус подобия - граничный диапазон для точек, включаемых в расчет размера корреляции. Значения по умолчанию основаны на ковариации сигнала.
Визуально исследуйте значения радиуса с помощью команды «Исследовать». Исследование показывает график зависимости интеграла корреляции от радиуса. Интеграл корреляции - это средняя вероятность того, что состояния системы близки в два различных временных интервала. Этот интеграл отражает самоподобие. Можно изменить диапазон подобия, переместив одну из вертикальных ограничивающих линий, как показано на следующем рисунке. Цель состоит в том, чтобы связать линейную часть кривой. При закрытии фигуры ограничивающие значения автоматически переносятся в параметры размера «Корреляция».
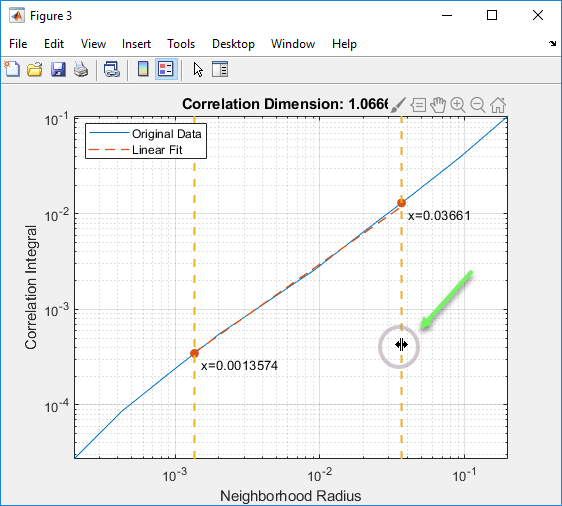
Количество точек - количество точек между значениями минимального и максимального диапазона. Этот параметр управляет разрешением расчета.
Дополнительные сведения об измерении корреляции см. в разделе correlationDimension.
Показатель Ляпунова измеряет степень хаоса из-за аномалии сигнала, исходя из скорости разделения бесконечно близких траекторий в фазовом пространстве. Ухудшение в системе увеличивает это значение. Положительная экспонента Ляпунова указывает на наличие хаоса, со степенью, связанной с величиной экспоненты. Отрицательная экспонента указывает на нехаотический сигнал.
Диапазон расширения - ограничивающий целочисленный диапазон, который ограничивает точки, используемые для оценки локальной скорости расширения. Затем эта скорость используется для вычисления показателя Ляпунова.
Визуально изучите взаимосвязь между диапазоном расширения и скоростью расширения (средняя логарифмическая дивергенция) с помощью команды Исследовать (Explore). Выберите линейную часть графика, используя целые числа для ограничения области. При закрытии фигуры ограничивающие значения автоматически переносятся в значения диапазона «Минимальное» и «Максимальное расширение».
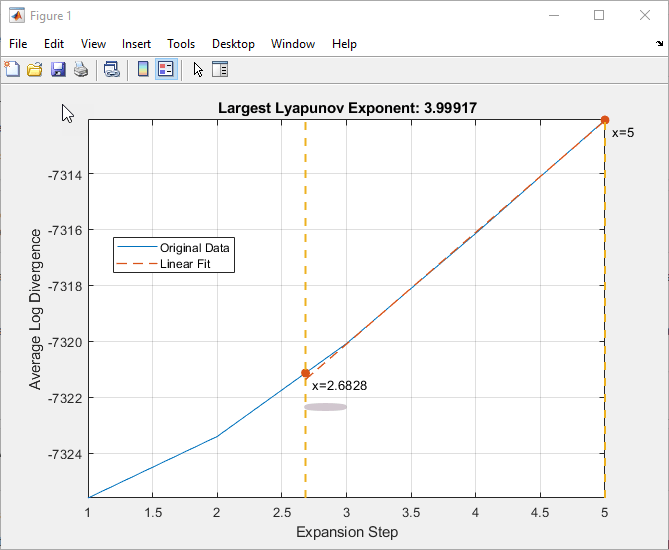
Средний период - пороговое целое значение, используемое для поиска ближайшего соседа для определенной точки для оценки наибольшей степени Ляпунова. Программное обеспечение основывает значение по умолчанию на средней частоте сигнала.
Дополнительные сведения о показателе Ляпунова см. в разделе lyapunovExponent.
Программа сохраняет результаты вычислений в новых элементах. Новые имена функций включают имя исходного сигнала с суффиксом nonlin.