Оптимальная конструкция фильтра FIR Паркса-Макклеллана
Используйте алгоритм Паркса-Макклеллана для проектирования полосового фильтра FIR порядка 17. Задайте нормированные частоты полосы останова и рад/образец и нормированные частоты полосы пропускания и рад/образец. Постройте график идеальных и фактических откликов величины.
f = [0 0.3 0.4 0.6 0.7 1]; a = [0 0 1 1 0 0]; b = firpm(17,f,a); [h,w] = freqz(b,1,512); plot(f,a,w/pi,abs(h)) legend('Ideal','firpm Design') xlabel 'Radian Frequency (\omega/\pi)', ylabel 'Magnitude'
Проектирование фильтра нижних частот с частотой отсечки полосы пропускания 1500 Гц и частотой отсечки полосы отсечки 2000 Гц. Укажите частоту дискретизации 8000 Гц. Требуется максимальная амплитуда полосы останова 0,01 и максимальная погрешность полосы пропускания (пульсация) 0,001. Получение требуемого порядка фильтрации, нормированных границ полосы частот, амплитуд полосы частот и весов с помощью firpmord.
[n,fo,ao,w] = firpmord([1500 2000],[1 0],[0.001 0.01],8000); b = firpm(n,fo,ao,w); fvtool(b,1)
Используйте алгоритм Паркса-Макклеллана для создания однополюсного полосного фильтра FIR 50-го порядка, который будет использоваться с сигналами, дискретизированными на частоте 1 кГц.
N = 50; Fs = 1e3;
Укажите, что полоса пропускания охватывает частоты от 200 Гц до 300 Гц и что переходная область на каждой стороне полосы пропускания имеет ширину 50 Гц.
Fstop1 = 150; Fpass1 = 200; Fpass2 = 300; Fstop2 = 350;
Сконструируйте фильтр таким образом, чтобы оптимизатор соответствовал весам низкочастотной стоп-полосы с весом 3, полосы пропускания с весом 1 и высокочастотной стоп-полосы с весом 100. Отображение амплитудной характеристики фильтра.
Wstop1 = 3;
Wpass = 1;
Wstop2 = 100;
b = firpm(N,[0 Fstop1 Fpass1 Fpass2 Fstop2 Fs/2]/(Fs/2), ...
[0 0 1 1 0 0],[Wstop1 Wpass Wstop2]);
fvtool(b,1)
Если конструкция фильтра не сходится, она может быть неправильной. Проверьте конструкцию, проверив частотную характеристику.
Если конструкция фильтра не сходится и результирующая конструкция фильтра неправильна, попробуйте выполнить одно или несколько из следующих действий.
Увеличьте порядок фильтрации.
Смягчить конструкцию фильтра путем уменьшения затухания в пробках и/или расширения переходных областей.
firpm создает линейный фильтр FIR с использованием алгоритма Паркса-Макклеллана [2]. Алгоритм Паркса-Макклеллана использует алгоритм обмена Ремеза и теорию аппроксимации Чебышёва для проектирования фильтров с оптимальным соответствием между желаемой и фактической частотными откликами. Фильтры являются оптимальными в том смысле, что максимальная ошибка между требуемой частотной характеристикой и фактической частотной характеристикой минимизируется. Фильтры, сконструированные таким образом, демонстрируют чёткое поведение в своих частотных откликах и иногда называются чёткими фильтрами. firpm проявляет разрывы в головке и хвосте своей импульсной характеристики из-за этой равнодействующей природы.
Это тип I (n нечетный) и тип II (n четные) линейно-фазовые фильтры. Векторы f и a задать частотно-амплитудные характеристики фильтра:
f - вектор пар частотных точек, заданный в диапазоне от 0 до 1, где 1 соответствует частоте Найквиста. Частоты должны быть в возрастающем порядке. Допускаются повторяющиеся частотные точки, которые фактически могут быть использованы для проектирования фильтра точно таким же образом, как те, которые возвращаются fir1 и fir2 функции с прямоугольником (rectwin) окно.
a - вектор, содержащий требуемую амплитуду в точках, указанных в f.
Желательной амплитудной функцией на частотах между парами точек (f (k) , f (k + 1)) для k нечетных является отрезок линии, соединяющий точки (f (k), a (k) и (f (k + 1), a (k + 1)).
Желательная амплитудная функция на частотах между парами точек (f (k) , f (k + 1)) для k четных не определена. Это переходные или «плевать» регионы.
f и a одинаковая длина. Эта длина должна быть четным числом.
На рисунке ниже показана взаимосвязь между f и a векторы при определении желаемой амплитудной характеристики.
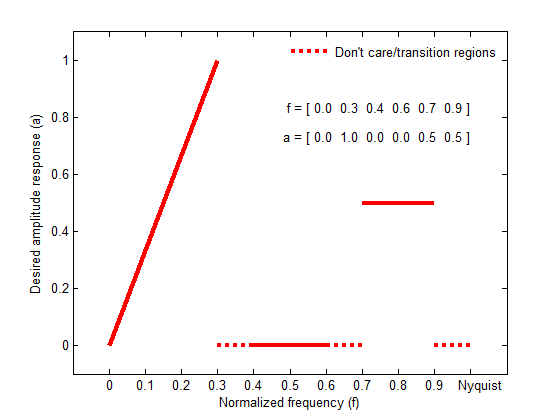
firpm всегда использует четный порядок фильтров для конфигураций с ровной симметрией и ненулевой полосой пропускания на частоте Найквиста. Причина четного порядка фильтрации заключается в том, что для импульсных откликов, проявляющих четную симметрию и нечетные порядки, частотная характеристика на частоте Найквиста обязательно равна 0. При указании нечетного значения n, firpm увеличивает его на 1.
firpm конструирует линейные фазовые фильтры типа I, II, III и IV. Тип I и тип II являются значениями по умолчанию для n даже и n нечетные, соответственно, в то время как тип III (n четные) и тип IV (n нечетные) указаны с помощью 'hilbert' или 'differentiator' , соответственно, используя ftype аргумент.. Различные типы фильтров имеют различные симметрии и определенные ограничения на их частотные характеристики. (Для получения дополнительной информации см. [3].)
| Тип фильтра линейной фазы | Порядок фильтрации | Симметрия коэффициентов | Ответ H (f), f = 0 | Ответ H (f), f = 1 (Найквист) |
|---|---|---|---|---|
Тип I | Даже | даже: 1,..., n + 1 | Без ограничений | Без ограничений |
Тип II | Странный | даже: 1,..., n + 1 | Без ограничений | H (1)
|
Тип III | Даже | нечетные: = 1,..., n + 1 | H (0) | H (1) |
| Тип IV | Странный | нечетные: = 1,..., n + 1 | H (0) | Без ограничений |
Также можно использовать firpm для записи функции, определяющей требуемую частотную характеристику. Предопределенный дескриптор функции частотной характеристики для firpm является @firpmfrf, который конструирует линейно-фазовый КИХ-фильтр.
Примечание
b = firpm(n,f,a,w) эквивалентно b = firpm(n,f,{@firpmfrf,a},w), где, @firpmfrf - предопределенный дескриптор функции частотной характеристики для firpm. При необходимости можно написать собственную функцию ответа. Использовать help
private/firpmfrf и см. раздел Создание дескриптора функции для получения дополнительной информации.
[1] Комитет по цифровой обработке сигналов Общества по акустической, речевой и сигнальной обработке IEEE, eds. Выбранные документы в цифровой обработке сигналов. Том II. Нью-Йорк: IEEE Press, 1976.
[2] Комитет по цифровой обработке сигналов Общества по акустической, речевой и сигнальной обработке IEEE, eds. Программы для цифровой обработки сигналов. Нью-Йорк: IEEE Press, 1979, алгоритм 5.1.
[3] Оппенгейм, Алан В., Рональд В. Шефер и Джон Р. Бак. Дискретно-временная обработка сигналов. Река Верхнее Седло, Нью-Джерси: Прентис Холл, 1999, с. 486.
[4] Парки, Томас В. и К. Сидни Беррус. Проектирование цифрового фильтра. Нью-Йорк: John Wiley & Sons, 1987, стр. 83.
[5] Рабинер, Лоуренс Р., Джеймс Х. Макклеллан и Томас В. Паркс. «Методы проектирования цифровых фильтров FIR с использованием взвешенного приближения Чебышева». Процедуры IEEE ®. Том 63, номер 4, 1975, стр. 595-610.
butter | cfirpm | cheby1 | cheby2 | ellip | fir1 | fir2 | fircls | fircls1 | firls | firpmord | rcosdesign | yulewalk