Exponenta Banner
exponenta event banner

istft

Обратное кратковременное преобразование Фурье

свернуть все на странице

Синтаксис

x = istft (s)
x = istft (s, fs)
x = istft (s, ts)
x = istft (___, имя, значение)
[x, t] = istft (___)

Описание

x = istft(s) возвращает обратное кратковременное преобразование Фурье (ISTFT) s.

пример

x = istft(s,fs) возвращает ISTFT s использование частоты выборки fs.

x = istft(s,ts) возвращает ISTFT с использованием времени выборки ts.

пример

x = istft(___,Name,Value) задает дополнительные параметры с использованием аргументов пары «имя-значение». Опции включают длину окна БПФ и количество перекрывающихся выборок. Эти аргументы можно добавить к любому из предыдущих входных синтаксисов.

пример

[x,t] = istft(___) возвращает время сигнала, при котором вычисляется ISTFT.

Примеры

свернуть все

Открыть сценарий в реальном времени

Генерируют трехканальный сигнал, состоящий из трех различных чирпов, дискретизированных на частоте 1 кГц в течение 1 секунды.

  1. Первый канал состоит из вогнутой квадратичной чирпы с мгновенной частотой 100 Гц при t = 0 и пересекает 300 Гц при t = 1 секунде. Имеет начальную фазу, равную 45 градусам.

  2. Второй канал состоит из выпуклой квадратичной чирпы с мгновенной частотой 200 Гц при t = 0 и пересекает 600 Гц при t = 1 секунде.

  3. Третий канал состоит из логарифмической чирпы с мгновенной частотой 300 Гц при t = 0 и пересекает 500 Гц при t = 1 секунде.

Вычисляют STFT многоканального сигнала, используя периодическое окно Хэмминга длиной 256 и длиной перекрытия 15 выборок.

fs = 1e3;
t = 0:1/fs:1-1/fs;
x = [chirp(t,100,1,300,'quadratic',45,'concave');
      chirp(t,200,1,600,'quadratic',[],'convex');
      chirp(t,300,1,500,'logarithmic')]'; 
  
[S,F,T] = stft(x,fs,'Window',hamming(256,'periodic'),'OverlapLength',15);

Постройте график оригинальных и реконструированных версий первого и второго каналов.

[ix,ti] = istft(S,fs,'Window',hamming(256,'periodic'),'OverlapLength',15);

plot(t,x(:,1)','LineWidth',1.5)
hold on
plot(ti,ix(:,1)','r--')
hold off
legend('Original Channel 1','Reconstructed Channel 1')

Figure contains an axes. The axes contains 2 objects of type line. These objects represent Original Channel 1, Reconstructed Channel 1.

plot(t,x(:,2)','LineWidth',1.5)
hold on
plot(ti,ix(:,2)','r--')

legend('Original Channel 2','Reconstructed Channel 2')

Figure contains an axes. The axes contains 2 objects of type line. These objects represent Original Channel 2, Reconstructed Channel 2.

Открыть сценарий в реальном времени

Фазовый вокодер выполняет растягивание времени и масштабирование основного тона путем преобразования звука в частотную область. На этой диаграмме показаны операции, связанные с реализацией фазового вокодера.

Фазовый вокодер принимает STFT сигнала с окном анализа размера транзитного участка R1 а затем выполняет ISTFT с окном синтеза R2 размера транзитного участка. Таким образом, вокодер использует преимущество способа WOLA. Чтобы растянуть сигнал во времени, окно анализа использует большее количество выборок перекрытия, чем синтез. В результате на выходе выборок больше, чем на входе (NS, Out > NS, In), хотя частотное содержание остается прежним. Теперь вы можете масштабировать этот сигнал, воспроизводя его с более высокой частотой дискретизации, что создает сигнал с исходной длительностью, но с более высоким шагом.

Загрузите аудиофайл, содержащий фрагмент «Hallelujah Chorus» Генделя с частотой 8192 Гц. 

load handel

Спроектируйте корневое окно Ханна длиной 512. Задайте для анализа длину перекрытия 192, а для синтеза - 166.

wlen = 512;
win = sqrt(hann(wlen,'periodic'));
noverlapA = 192;
noverlapS = 166;

Реализовать фазовый вокодер с использованием окна анализа перекрытия 192 и окна синтеза перекрытия 166. 

S = stft(y,Fs,'Window',win,'OverlapLength',noverlapA);
iy = istft(S,Fs,'Window',win,'OverlapLength',noverlapS);


%To hear, type soundsc(w,Fs), pause(10), soundsc(iw,Fs);

Если окна анализа и синтеза одинаковы, но длина перекрытия изменена, появится дополнительный выигрыш/убыток, который необходимо скорректировать. Это общий подход к реализации фазового вокодера.

Вычислите коэффициент перехода и используйте его для регулировки усиления восстановленного сигнала. Вычисляют также частоту данных со сдвигом основного тона с использованием коэффициента скачкообразного изменения.

hopRatio = (wlen-noverlapS)/(wlen-noverlapA);
iyg = iy*hopRatio;
Fp = Fs*hopRatio;


%To hear, type soundsc(iwg,Fs), pause(15), soundsc(iwg,Fp);

Постройте график исходного сигнала и растянутого во времени сигнала с фиксированным усилением.

plot((0:length(iyg)-1)/Fs,iyg,(0:length(y)-1)/Fs,y)
xlabel('Time (s)')
xlim([0 (length(iyg)-1)/Fs])
legend('Time Stretched Signal with Fixed Gain','Original Signal','Location','best')

Figure contains an axes. The axes contains 2 objects of type line. These objects represent Time Stretched Signal with Fixed Gain, Original Signal.

Сравните растянутый по времени сигнал и сдвинутый по тангажу сигнал на одном и том же графике.

plot((0:length(iy)-1)/Fs,iy,(0:length(iy)-1)/Fp,iy)
xlabel('Time (s)')
xlim([0 (length(iyg)-1)/Fs])
legend('Time Stretched Signal','Pitch Shifted Signal','Location','best')

Figure contains an axes. The axes contains 2 objects of type line. These objects represent Time Stretched Signal, Pitch Shifted Signal.

Чтобы лучше понять эффект данных сдвига основного тона, рассмотрим следующую синусоиду частоты Fs более 2 секунд.

t =  0:1/Fs:2;
x = sin(2*pi*10*t);

Вычислите кратковременное преобразование Фурье и обратное кратковременное преобразование Фурье с длинами наложения 192 и 166 соответственно.

Sx = stft(x,Fs,'Window',win,'OverlapLength',noverlapA);
ix = istft(Sx,Fs,'Window',win,'OverlapLength',noverlapS);

Постройте график исходного сигнала на одном графике и растянутого во времени и сдвинутого по тангажу сигнала на другом.

subplot(2,1,1)
plot((0:length(ix)-1)/Fs,ix,'LineWidth',2) 
xlabel('Time (s)')
ylabel('Signal Amplitude')
xlim([0 (length(ix)-1)/Fs])
legend('Time Stretched Signal') 



subplot(2,1,2)
hold on
plot((0:length(x)-1)/Fs,x)
plot((0:length(ix)-1)/Fp,ix,'--','LineWidth',2)
legend('Original Signal','Pitch Shifted Signal','Location','best')
hold off
xlabel('Time (s)')
ylabel('Signal Amplitude')
xlim([0 (length(ix)-1)/Fs])

Figure contains 2 axes. Axes 1 contains an object of type line. This object represents Time Stretched Signal. Axes 2 contains 2 objects of type line. These objects represent Original Signal, Pitch Shifted Signal.

Открыть сценарий в реальном времени

Создайте комплексную синусоиду частотой 1 кГц и длительностью 2 секунды.

fs = 1e3;
ts = 0:1/fs:2-1/fs;

x = exp(2j*pi*100*cos(2*pi*2*ts));

Спроектируйте периодическое окно Ганна длиной 100 и установите количество выборок перекрытия равным 75. Проверьте соответствие COLA в окне и длину перекрытия.

nwin = 100;
win = hann(nwin,'periodic');
noverlap = 75;

tf = iscola(win,noverlap)
tf = logical
   1

Нулевая вставка сигнала для удаления краевых эффектов. Чтобы избежать усечения, заполните входной сигнал нулями, чтобы

длина (xZero) -noverlapnwin-noverlapSignal длина минус перекрытие по длине окна минус перекрытие

- целое число. Установите длину БПФ равной 128. Вычислите кратковременное преобразование Фурье комплексного сигнала.

nPad = 100;
xZero = [zeros(1,nPad) x zeros(1,nPad)];
fftlen = 128;
s = stft(xZero,fs,'Window',win,'OverlapLength',noverlap,'FFTLength',fftlen);

Вычислите обратное кратковременное преобразование Фурье и удалите нули для идеальной реконструкции.

[is,ti] = istft(s,fs,'Window',win,'OverlapLength',noverlap,'FFTLength',fftlen);
is(1:nPad) = [];
is(end-nPad+1:end) = [];
ti = ti(1:end-2*nPad);

Постройте график реальных частей исходных и реконструированных сигналов. Мнимая часть сигнала также восстанавливается идеально.

plot(ts,real(x))
hold on
plot(ti,real(is),'--')
xlim([0 0.5])
xlabel('Time (s)')
ylabel('Amplitude (V)')
legend('Original Signal','Reconstructed Signal') 
hold off

Figure contains an axes. The axes contains 2 objects of type line. These objects represent Original Signal, Reconstructed Signal.

Открыть сценарий в реальном времени

Генерируют синусоиду, отобранную при частоте 2 кГц в течение 1 секунды.

fs = 2e3;
t = 0:1/fs:1-1/fs;
x = 5*sin(2*pi*10*t);

Создание периодического окна Хэмминга длиной 120. Проверьте ограничение COLA для окна с перекрытием 80 выборок. Комбинация «окно-перекрытие» совместима с COLA.

win = hamming(120,'periodic');
noverlap = 80;
tf = iscola(win,noverlap)
tf = logical
   1

Установите длину БПФ равной 512. Вычислите кратковременное преобразование Фурье.

fftlen = 512;
s = stft(x,fs,'Window',win,'OverlapLength',noverlap,'FFTLength',fftlen);

Вычислите обратное кратковременное преобразование Фурье.

[X,T] = istft(s,fs,'Window',win,'OverlapLength',noverlap,'FFTLength',fftlen,'Method','ola','ConjugateSymmetric',true);

Постройте график исходных и восстановленных сигналов.

plot(t,x,'b')
hold on
plot(T,X,'-.r')
xlabel('Time (s)')
ylabel('Amplitude (V)')
title('Original and Reconstructed Signal')
legend('Original Signal','Reconstructed Signal')
hold off

Figure contains an axes. The axes with title Original and Reconstructed Signal contains 2 objects of type line. These objects represent Original Signal, Reconstructed Signal.

Входные аргументы

свернуть все

Кратковременное преобразование Фурье, указанное как матрица или 3-D массив. Для одноканальных сигналов укажите s как матрица с увеличением времени по столбцам и увеличением частоты по строкам. Для многоканальных сигналов укажите s как массив 3-D с третьим размером, соответствующим каналам. Частотные и временные векторы получаются как выходы stft.

Примечание

Если инвертировать s использование istft и хотите, чтобы результат был такой же длины, как x, значение (length(x)-noverlap)/(length(window)-noverlap) должно быть целым числом.

Типы данных: double | single
Поддержка комплексного номера: Да

Частота выборки в герцах, заданная как положительный скаляр.

Типы данных: double | single

Время выборки, указанное как duration скаляр.

Пример: seconds(1) является duration скаляр, представляющий 1-секундную разность времени между последовательными выборками сигнала.

Типы данных: duration

Аргументы пары «имя-значение»

Укажите дополнительные пары, разделенные запятыми Name,Value аргументы. Name является именем аргумента и Value - соответствующее значение. Name должен отображаться внутри кавычек. Можно указать несколько аргументов пары имен и значений в любом порядке как Name1,Value1,...,NameN,ValueN.

Пример: istft(s,'Window',win,'OverlapLength',50,'FFTLength',128) окна данных с помощью окна win50 выборок перекрываются между соседними сегментами и 128 точками DFT.

Оконная функция, заданная как разделенная запятыми пара, состоящая из 'Window' и вектор. Если окно не указано или указано как пустое, функция использует периодическое окно Ганна длиной 128. Длина Window должно быть больше или равно 2.

Список доступных окон см. в разделе Windows.

Пример: hann(N+1) и (1-cos(2*pi*(0:N)'/N))/2 оба задают окно Ганна длиной N  + 1.

Типы данных: double | single

Количество перекрывающихся выборок, указанных как пара, разделенная запятыми, состоящая из 'OverlapLength' и положительное целое число, меньшее длины window. Если опустить 'OverlapLength' или указать его как пустое, оно устанавливается в наибольшее целое число менее 75% длины окна, которое оказывается 96 выборок для окна Ханна по умолчанию.

Типы данных: double | single

Количество точек DFT, указанных как разделенная запятыми пара, состоящая из 'FFTLength' и положительное целое число. Чтобы достичь идеальной реконструкции временной области, необходимо задать количество точек DFT, соответствующее используемому в stft.

Типы данных: double | single

Метод наложения-добавления, указанный как пара, разделенная запятыми, состоящая из 'Method' и один из них:

  • 'wola' - Взвешенное перекрытие - добавление

  • 'ola' - Наложение-добавление

Сопряженная симметрия исходного сигнала, определяемая как разделенная запятыми пара, состоящая из 'ConjugateSymmetric' и true или false. Если для этой опции установлено значение true, istft предполагает, что входные данные s является симметричным, иначе симметричное предположение не делается. Когда s не является точно симметричным сопряжением из-за ошибки округления, устанавливая для пары имя-значение значение true гарантирует, что STFT будет обрабатываться, как если бы он был сопряженным симметричным. Если s является сопряженным симметричным, тогда вычисление обратного преобразования происходит быстрее, а выход является реальным.

Частотный диапазон STFT, определяемый как разделенная запятыми пара, состоящая из 'FrequencyRange' и 'centered', 'twosided', или 'onesided'.

  • 'centered' - Лечить s как двусторонний, центрированный STFT. Если nfft является четным, то s считается вычисленным по интервалу (-δ, δ] рад/выборка. Если nfft является нечетным, то s считается вычисленным по интервалу (-δ, δ) рад/выборка. Если указать временную информацию, то интервалы будут (-fs, fs/2] циклами/единичным временем и (-fs, fs/2) циклами/единичным временем соответственно, где fs - частота выборки.

  • 'twosided' - Лечить s как двусторонний STFT, вычисленный на интервале [0, 2δ) рад/выборка. Если указать информацию о времени, то интервал будет равен [0, fs) циклам/единицам времени.

  • 'onesided' - Лечить s как односторонний STFT. Если nfft является четным, то s считается вычисленным за интервал [0, δ] рад/выборка. Если nfft является нечетным, то s считается вычисленным за интервал [0, δ) рад/выборка. При указании временной информации интервалы составляют [0, fs/2] циклов/единичного времени и [0, fs/2) циклов/единичного времени соответственно, где fs - частота выборки.

    Примечание

    Если для этого аргумента установлено значение 'onesided', istft предполагает, что значения в положительном диапазоне Найквиста были вычислены без сохранения общей мощности.

Пример см. в разделе Диапазоны частот STFT.

Типы данных: char | string

Измерение входного времени, указанное как пара, разделенная запятыми, состоящая из 'InputTimeDimension' и 'acrosscolumns' или 'downrows'. Если это значение равно 'downrows', istft предполагает, что измерение времени s находится вниз по строкам, а частота по столбцам. Если это значение равно 'acrosscolumns', функция istft предполагает, что измерение времени s находится поперек столбцов, а измерение частоты - вниз по строкам.

Выходные аргументы

свернуть все

Восстановленный сигнал во временной области, возвращаемый как вектор или матрица.

Типы данных: single | double

Моменты времени, возвращенные как вектор.

  • Если частота выборки fs обеспечивается, то t содержит значения времени в секундах.

  • Если длительность ts обеспечивается, то t имеет тот же формат времени, что и длительность ввода, и является массивом длительности.

  • Если информация о времени не предоставляется, то t содержит номера образцов.

Типы данных: double | single

Подробнее

свернуть все

Обратное короткое преобразование Фурье

Обратное кратковременное преобразование Фурье вычисляется путем взятия IFFT каждого вектора DFT STFT и наложения-сложения инвертированных сигналов. ISTFT рассчитывается следующим образом:

x (n) =∫−1/21/2∑m=−∞∞Xm (f) ej2πfndf=∑m=−∞∞∫−1/21/2Xm (f) ej2πfndf=∑m=−∞∞xm (n)

где R - размер транзитного участка между последовательными DFT, Xm - DFT оконных данных, центрированных относительно времени mR и xm (n) = x (n) g (n − mR). Обратная STFT является совершенной реконструкцией исходного сигнала до тех пор, пока ∑m=−∞∞ga+1 (n − mR) = c ∀n∈ℤ где окно g (n) анализа использовалось для окнивания исходного сигнала, а c является константой. На следующем рисунке показаны шаги, выполняемые при восстановлении исходного сигнала.

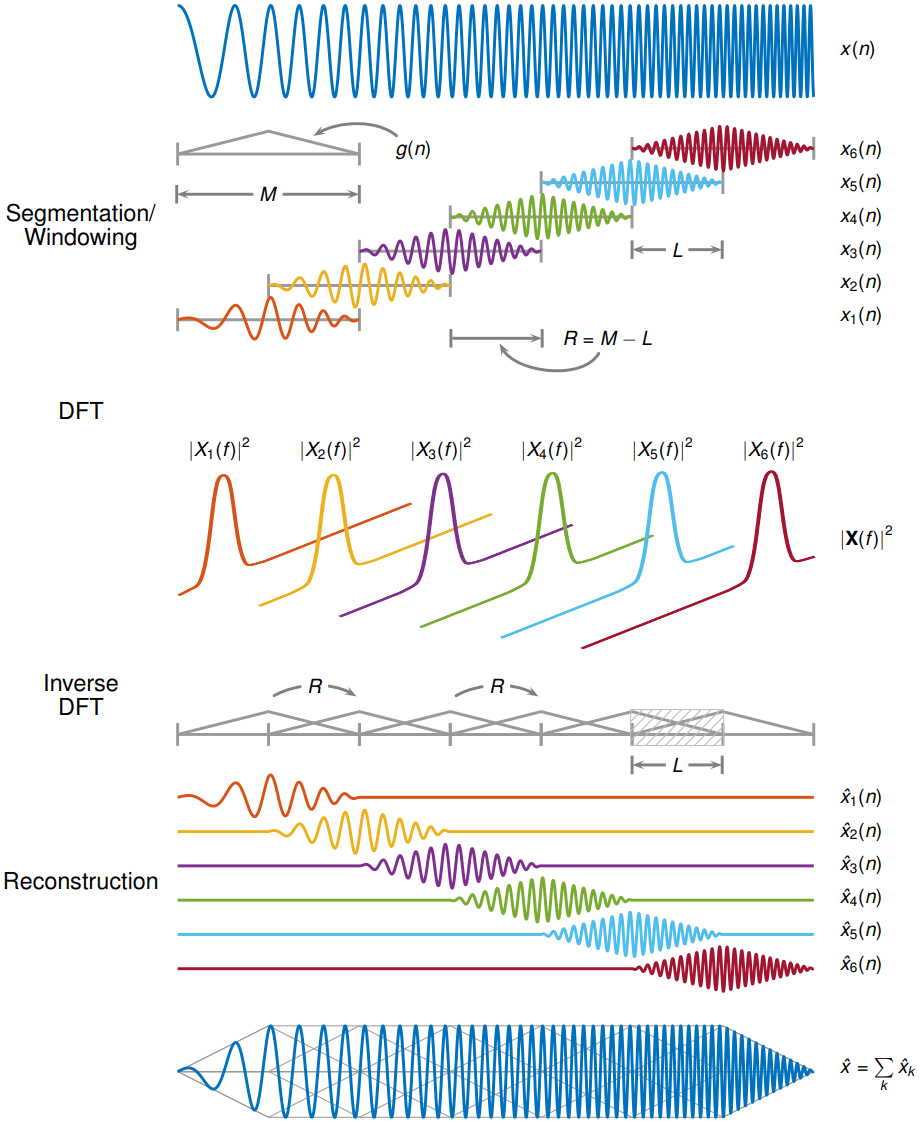
Ограничение «Постоянное перекрытие - добавление» (COLA)

Для обеспечения успешной реконструкции немодифицированных спектров окно анализа должно удовлетворять ограничению COLA. В общем случае, если окно анализа удовлетворяет условию ∑m=−∞∞ga+1 (n − mR) = c ∀n∈ℤ, окно считается совместимым с COLA. Кроме того, соответствие COLA может быть охарактеризовано как слабое или сильное.

  • Слабое соответствие COLA подразумевает, что преобразование Фурье окна анализа имеет нули на гармониках частоты кадров, так что

    G (fk) = 0, k = 1,2,..., R − 1, fk≜kR.

    Подавление псевдонима нарушается спектральными модификациями. Слабый COLA полагается на отмену псевдонима в частотной области. Следовательно, идеальная реконструкция возможна с использованием слабо совместимых с COLA окон до тех пор, пока сигнал не претерпел никаких спектральных модификаций.

  • Для строгого соответствия COLA преобразование Фурье окна должно быть ограничено полосой пропускания последовательно с понижением дискретизации на частоту кадров, так что

    G (f) = 0, f≥12R.

    Это уравнение показывает, что строгое ограничение COLA не допускает наложения псевдонимов. Кроме того, для сильного соответствия COLA значение константы c должно быть равно 1. В общем случае, если короткий временной спектр каким-либо образом модифицирован, предпочтительнее более сильное окно, совместимое с COLA.

Вы можете использовать iscola функция для проверки на слабое соответствие COLA. Количество сумм, используемых для проверки соответствия COLA, определяется длиной окна и размером транзитного участка. В общем, обычно используется a = 1 в ∑m=−∞∞ga+1 (n − mR) = c ∀n∈ℤ для взвешенного наложения-сложения (WOLA) и a = 0 для наложения-сложения (OLA). По умолчаниюistft использует метод WOLA, применяя окно синтеза перед выполнением метода наложения-добавления.

Как правило, окно синтеза совпадает с окном анализа. Можно создать полезные окна WOLA, взяв квадратный корень сильного окна OLA. Этот метод можно использовать для всех неотрицательных окон OLA. Например, корневое окно Ханна является хорошим примером окна WOLA.

Идеальная реконструкция

В общем, вычисление STFT входного сигнала и инвертирование его не приводит к идеальной реконструкции. Если выход ISTFT должен максимально соответствовать исходному входному сигналу, сигнал и окно должны удовлетворять следующим условиям:

  • Размер ввода - если инвертировать вывод stft использование istft и хотите, чтобы результат был той же длины, что и входной сигнал x, значение k = (length (x) -noverlap) (length (window) -noverlap) должно быть целым числом.

  • Соответствие COLA - используйте окна, совместимые с COLA, предполагая, что вы не изменили кратковременное преобразование Фурье сигнала.

  • Заполнение - Если длина входного сигнала такова, что значение k не является целым числом, то перед вычислением кратковременного преобразования Фурье сигнал заполняется нулем. Удалите дополнительные нули после инвертирования сигнала.

Ссылки

[1] Крохьер, Р. Е. «Метод взвешенного перекрытия-добавления кратковременного анализа/синтеза Фурье». Транзакции IEEE по акустике, обработке речи и сигналов. Том 28, номер 1, февраль 1980 года, стр. 99-102.

[2] Готцен, А. Д., Н. Бернардини и Д. Арфиб. «Традиционные реализации фазового вокодера: хитрости торговли». Материалы Конференции COST G-6 по цифровым звуковым эффектам (DAFX-00), Верона, Италия, 7-9 декабря 2000 года.

[3] Гриффин, Дэниел У. и Чжэ С. Лим. «Оценка сигнала из модифицированного кратковременного преобразования Фурье». Транзакции IEEE по акустике, обработке речи и сигналов. Том 32, номер 2, апрель 1984, стр. 236-243.

[4] Портнофф, М. Р. «Частотно-временное представление цифровых сигналов и систем на основе краткосрочного анализа Фурье». Транзакции IEEE по акустике, обработке речи и сигналов. Том 28, номер 1, февраль 1980 года, стр. 55-69.

[5] Смит, Джулиус Орион. Обработка спектрального аудиосигнала. https://ccrma.stanford.edu/~jos/sasp/, интернет-книга, издание 2011 года, вышел в ноябре 2018 года.

[6] Шарп, Брюс. Обратимость наложения - добавление обработки. https://gauss256.github.io/blog/cola.html, получил доступ в июле 2019 года.

Расширенные возможности

..

См. также

Функции

Темы

Представлен в R2019a

Документация по инструментам обработки сигналов

Поддержка