Кратковременное преобразование Фурье
s = stft(___,Name,Value)
stft(___) без выходных аргументов отображает величину STFT в текущем окне рисунка.
Создайте две секунды выходного сигнала генератора, управляемого напряжением, управляемого синусоидой, дискретизированной на частоте 10 кГц.
fs = 10e3; t = 0:1/fs:2; x = vco(sin(2*pi*t),[0.1 0.4]*fs,fs);
Вычислите и постройте график STFT сигнала. Используйте окно Кайзера длиной 256 и параметром формы 5. Укажите длину перекрытия в виде 220 выборок и длину DFT в виде 512 точек. Постройте график STFT с картой цветов и видом по умолчанию.
stft(x,fs,'Window',kaiser(256,5),'OverlapLength',220,'FFTLength',512);

Измените вид для отображения STFT в виде графика водопада. Задайте для карты цветов значение jet.
view(-45,65)
colormap jet
Создайте квадратичную чирп-схему с частотой 1 кГц в течение 2 секунд. Мгновенная частота составляет 100 Гц при 0 и пересекает 200 Гц = 1 секунда.
ts = 0:1/1e3:2; f0 = 100; f1 = 200; x = chirp(ts,f0,1,f1,'quadratic',[],'concave');
Вычислите и отобразите STFT квадратичного чирпа длительностью 1 мс.
d = seconds(1e-3); win = hamming(100,'periodic'); stft(x,d,'Window',win,'OverlapLength',98,'FFTLength',128);

Генерация сигнала с частотой 5 кГц в течение 4 секунд. Сигнал состоит из набора импульсов уменьшающейся длительности, разделенных областями колебательной амплитуды и флуктуационной частоты с тенденцией увеличения. Постройте график сигнала.
fs = 5000; t = 0:1/fs:4-1/fs; x = besselj(0,600*(sin(2*pi*(t+1).^3/30).^5)); plot(t,x)

Вычислите односторонние, двусторонние и центрированные краткосрочные преобразования Фурье сигнала. Во всех случаях используйте 202-образное окно Кайзера с коэффициентом формы 10, чтобы открыть сегменты сигнала. Отображение частотного диапазона, используемого для вычисления каждого преобразования.
rngs = ["onesided" "twosided" "centered"]; for kj = 1:length(rngs) opts = {'Window',kaiser(202,10),'FrequencyRange',rngs(kj)}; [~,f] = stft(x,fs,opts{:}); subplot(length(rngs),1,kj) stft(x,fs,opts{:}) title(sprintf('''%s'': [%5.3f, %5.3f] kHz',rngs(kj),[f(1) f(end)]/1000)) end
![Figure contains 3 axes. Axes 1 with title 'onesided': [0.000, 2.500] kHz contains an object of type image. Axes 2 with title 'twosided': [0.000, 4.975] kHz contains an object of type image. Axes 3 with title 'centered': [-2.475, 2.500] kHz contains an object of type image.](../../examples/signal/win64/STFTFrequencyRangesExample_02.png)
Повторите вычисления, но теперь измените длину окна Кайзера на 203, нечетное число. 'twosided' частотный интервал не изменяется. Два других частотных интервала становятся открытыми на верхнем конце.
for kj = 1:length(rngs) opts = {'Window',kaiser(203,10),'FrequencyRange',rngs(kj)}; [~,f] = stft(x,fs,opts{:}); subplot(length(rngs),1,kj) stft(x,fs,opts{:}) title(sprintf('''%s'': [%5.3f, %5.3f] kHz',rngs(kj),[f(1) f(end)]/1000)) end
![Figure contains 3 axes. Axes 1 with title 'onesided': [0.000, 2.488] kHz contains an object of type image. Axes 2 with title 'twosided': [0.000, 4.975] kHz contains an object of type image. Axes 3 with title 'centered': [-2.488, 2.488] kHz contains an object of type image.](../../examples/signal/win64/STFTFrequencyRangesExample_03.png)
Генерируют трехканальный сигнал, состоящий из трех различных чирпов, дискретизированных на частоте 1 кГц в течение одной секунды.
Первый канал состоит из вогнутой квадратичной чирпы с мгновенной частотой 100 Гц при t = 0 и пересекает 300 Гц при t = 1 секунде. Имеет начальную фазу, равную 45 градусам.
Второй канал состоит из выпуклой квадратичной чирпы с мгновенной частотой 100 Гц при t = 0 и пересекает 500 Гц при t = 1 секунде.
Третий канал состоит из логарифмической чирпы с мгновенной частотой 300 Гц при t = 0 и пересекает 500 Гц при t = 1 секунде.
Вычисляют STFT многоканального сигнала, используя периодическое окно Хэмминга длиной 128 и длиной перекрытия 50 выборок.
fs = 1e3; t = 0:1/fs:1-1/fs; x = [chirp(t,100,1,300,'quadratic',45,'concave'); chirp(t,100,1,500,'quadratic',[],'convex'); chirp(t,300,1,500,'logarithmic')]'; [S,F,T] = stft(x,fs,'Window',hamming(128,'periodic'),'OverlapLength',50);
Визуализировать STFT каждого канала как график водопада. Управление поведением осей с помощью вспомогательной функции helperGraphicsOpt.
waterfall(F,T,abs(S(:,:,1))') helperGraphicsOpt(1)

waterfall(F,T,abs(S(:,:,2))') helperGraphicsOpt(2)

waterfall(F,T,abs(S(:,:,3))') helperGraphicsOpt(3)

Эта вспомогательная функция задает внешний вид и поведение текущих осей.
function helperGraphicsOpt(ChannelId) ax = gca; ax.XDir = 'reverse'; ax.ZLim = [0 30]; ax.Title.String = ['Input Channel: ' num2str(ChannelId)]; ax.XLabel.String = 'Frequency (Hz)'; ax.YLabel.String = 'Time (seconds)'; ax.View = [30 45]; end
x - Входной сигналВходной сигнал, заданный как вектор, матрица или MATLAB
®timetable.
Примечание
Если инвертировать s использование istft и хотите, чтобы результат был такой же длины, как x, значение (length(x)-noverlap)/(length(window)-noverlap) должно быть целым числом.
Если вход имеет несколько каналов, укажите x в качестве матрицы, где каждый столбец соответствует каналу.
Для ввода расписания, x должен содержать равномерно увеличивающиеся конечные времена строк. Если расписание имеет отсутствующие или повторяющиеся моменты времени, его можно исправить с помощью подсказок в «Чистом расписании» с «Отсутствующим», «Повторяющимся» или «Неуниформным временем».
Для ввода многоканального расписания укажите x как расписание с одной переменной, содержащей матрицу, или расписание с несколькими переменными, каждая из которых содержит вектор-столбец. Все переменные должны иметь одинаковую точность.
Каждый канал x должна иметь длину, большую или равную длине окна.
Пример: chirp(0:1/4e3:2,250,1,500,'quadratic') задает одноканальную частотную частоту.
Пример: timetable(rand(5,2),'SampleRate',1) задает двухканальную случайную величину, дискретизированную с частотой 1 Гц в течение 4 секунд.
Пример: timetable(rand(5,1),rand(5,1),'SampleRate',1) задает двухканальную случайную величину, дискретизированную с частотой 1 Гц в течение 4 секунд.
Типы данных: double | single
Поддержка комплексного номера: Да
fs - Частота выборки2π (по умолчанию) | положительный скалярЧастота выборки, заданная как положительный скаляр. Этот аргумент применяется только в том случае, если x - вектор или матрица.
Типы данных: double | single
ts - Время выборкиУкажите дополнительные пары, разделенные запятыми Name,Value аргументы. Name является именем аргумента и Value - соответствующее значение. Name должен отображаться внутри кавычек. Можно указать несколько аргументов пары имен и значений в любом порядке как Name1,Value1,...,NameN,ValueN.
'Window',hamming(100),'OverlapLength',50,'FFTLength',128 окошивает данные, используя 100-образное окно Хэмминга, с 50 выборками перекрытия между соседними сегментами и 128-точечным БПФ.'Window' - Спектральное окноhann(128,'periodic') (по умолчанию) | векторСпектральное окно, указанное как вектор. Если окно не указано или указано как пустое, функция использует окно Ганна длиной 128. Длина 'Window' должно быть больше или равно 2.
Список доступных окон см. в разделе Windows.
Пример: hann(N+1) и (1-cos(2*pi*(0:N)'/N))/2 оба задают окно Ганна длиной N + 1.
Типы данных: double | single
'OverlapLength' - Количество перекрывающихся образцов75% длины окна (по умолчанию) | неотрицательное целое числоЧисло перекрывающихся выборок, указанное как положительное целое число, меньшее длины 'Window'. Если опустить 'OverlapLength' или укажите его как пустое, оно будет иметь наибольшее целое число менее 75% длины окна, что составляет 96 выборок для окна Ханна по умолчанию.
Типы данных: double | single
'FFTLength' - Количество точек DFT128 (по умолчанию) | положительное целое числоЧисло точек DFT, указанное как положительное целое число. Значение должно быть больше или равно длине окна. Если длина входного сигнала меньше длины DFT, данные заполняются нулями.
Типы данных: double | single
'FrequencyRange' - диапазон частот STFT'centered' (по умолчанию) | 'twosided' | 'onesided'Диапазон частот STFT, указанный как 'centered', 'twosided', или 'onesided'.
'centered' - Вычислить двусторонний центрированный STFT. Если 'FFTLength' является четным, то s вычисляется по интервалу (-δ, δ] рад/выборка. Если 'FFTLength' является нечетным, то s вычисляется по интервалу (-δ, δ) рад/выборка. Если указать временную информацию, то интервалы будут (-fs, fs/2] циклами/единичным временем и (-fs, fs/2) циклами/единичным временем соответственно, где fs - эффективная частота выборки.
'twosided' - Вычислить двусторонний STFT на интервале [0, 2δ) рад/выборка. Если указать информацию о времени, то интервал будет равен [0, fs) циклам/единицам времени.
'onesided' - вычислить односторонний STFT. Если 'FFTLength' является четным, то s вычисляется по интервалу [0, δ] рад/выборка. Если 'FFTLength' является нечетным, то s вычисляется по интервалу [0, δ) рад/выборка. При указании временной информации интервалы составляют [0, fs/2] циклов/единичного времени и [0, fs/2) циклов/единичного времени соответственно, где fs - эффективная частота выборки. Эта опция действительна только для реальных сигналов.
Примечание
Если для этого аргумента установлено значение 'onesided', stft выводит значения в положительном диапазоне Найквиста и не сохраняет общую мощность.
Пример см. в разделе Диапазоны частот STFT.
Типы данных: char | string
'OutputTimeDimension' - Измерение времени вывода'acrosscolumns' (по умолчанию) | 'downrows'Измерение времени вывода, указанное как 'acrosscolumns' или 'downrows'. Задайте для этого значения значение 'downrows' если требуется измерение времени s вниз по строкам и размерности частоты по столбцам. Задайте для этого значения значение 'acrosscolumns' если требуется измерение времени s по столбцам и размерности частоты вниз по строкам. Этот ввод игнорируется, если функция вызывается без выходных аргументов.
s - Кратковременное преобразование ФурьеКратковременное преобразование Фурье, возвращаемое в виде матрицы или массива 3-D. Время увеличивается по столбцам s и частота увеличивается вниз по строкам. Третье измерение, если оно имеется, соответствует входным каналам.
Если сигнал x имеет Nx отсчетов времени, то s имеет k столбцов, где k = ⌊ (Nx-L )/( M-L) ⌋, M - длина'Window', L - 'OverlapLength'и символы ⌊ ⌋ обозначают функцию пола.
Количество строк в s равно значению, указанному в 'FFTLength'.
Типы данных: double | single
f - ЧастотыЧастоты, на которых вычисляется STFT, возвращаются в виде вектора.
Типы данных: double | single
t - Временные моментыМоменты времени, возвращенные как вектор. t содержит значения времени, соответствующие центрам сегментов данных, используемых для вычисления краткосрочных оценок спектра мощности.
Типы данных: double | single
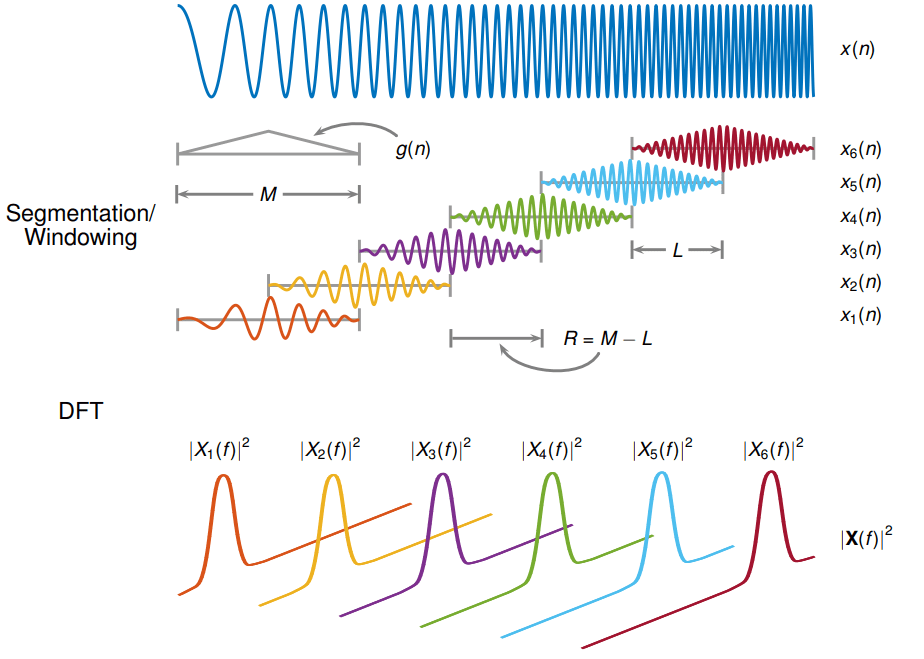
Кратковременное преобразование Фурье (STFT) используется для анализа того, как частотное содержание нестационарного сигнала изменяется во времени.
STFT сигнала вычисляется путем перемещения окна анализа длиной по сигналу и вычисления дискретного преобразования Фурье оконных данных. Окно перескакивает по исходному сигналу с интервалами выборок. Большинство оконных функций сужаются по краям, чтобы избежать спектрального звонка. Если задана ненулевая длина L перекрытия, то добавление сегментов с перекрытием компенсирует ослабление сигнала на краях окна. ДПФ каждого оконного сегмента добавляется к матрице, которая содержит величину и фазу для каждого момента времени и частоты. Количество строк в STFT-матрице равно количеству точек DFT, а количество столбцов задается
⌋,
где - длина исходного сигнала ), а символы ⌊ ⌋ обозначают функцию пола.
Матрица STFT задается X ) ⋯Xk (f)] таким образом, что m-й элемент этой матрицы является
e − j2āfn,
где
) - Оконная функция длины М.
) - DFT оконных данных, центрированных относительно времени mR.
- Размер транзитного участка между последовательными DFT. Размер транзитного участка представляет собой разницу между длиной окна Mand и длиной перекрытия .
Величина в квадрате STFT дает spectrogram представление спектральной плотности мощности функции.
В общем, вычисление STFT входного сигнала и инвертирование его не приводит к идеальной реконструкции. Если выход ISTFT должен максимально соответствовать исходному входному сигналу, сигнал и окно должны удовлетворять следующим условиям:
Размер ввода - если инвертировать вывод stft использование istft и хотите, чтобы результат был той же длины, что и входной сигнал x, значение noverlap) должно быть целым числом.
Соответствие COLA - используйте окна, совместимые с COLA, предполагая, что вы не изменили кратковременное преобразование Фурье сигнала.
Заполнение - Если длина входного сигнала такова, что значение k не является целым числом, то перед вычислением кратковременного преобразования Фурье сигнал заполняется нулем. Удалите дополнительные нули после инвертирования сигнала.
[1] Митра, Санджит К. Цифровая обработка сигналов: компьютерный подход. 2-й ред. Нью-Йорк: Макгроу-Хилл, 2001.
[2] Шарп, Брюс. Обратимость наложения - добавление обработки. https://gauss256.github.io/blog/cola.html, получил доступ в июле 2019 года.
[3] Смит, Джулиус Орион. Обработка спектрального аудиосигнала. https://ccrma.stanford.edu/~jos/sasp/, интернет-книга, издание 2011 года, доступ к ноябрю 2018 года.
Примечания и ограничения по использованию:
'OutputTimeDimension' всегда должен быть указан и установлен в значение 'downrows'.
Дополнительные сведения см. в разделе Массивы Tall.
Примечания и ограничения по использованию:
Расписания не поддерживаются для создания кода.
Примечания и ограничения по использованию:
Расписания не поддерживаются для создания кода.
Эта функция полностью поддерживает массивы графических процессоров. Дополнительные сведения см. в разделе Запуск функций MATLAB на графическом процессоре (панель инструментов параллельных вычислений).
Имеется измененная версия этого примера. Открыть этот пример с помощью изменений?
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.