Оптимизация конструкции в соответствии с требованиями к ступенчатому реагированию (код)

В этом примере показано, как программно оптимизировать параметры контроллера в соответствии с требованиями ответа на шаг с помощью sdo.optimize функция.

Структура модели

Модель Simulink ®watertank_stepinput включает в себя установку нелинейной системы водоемов и ПИ-контроллер в одноконтурной системе обратной связи.

Блок Step применяет ввод шага. Для оптимизации отклика, генерируемого такими входами, можно также использовать другие типы входных данных, такие как наклонные.

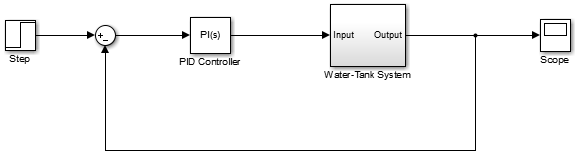
На этом рисунке показана система резервуаров для воды.

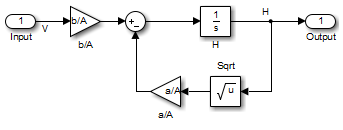
Вода поступает в бак наверху со скоростью, пропорциональной открытию клапана. Открытие клапана пропорционально напряжению В, приложенному к насосу. Вода выходит через отверстие в основании резервуара со скоростью, пропорциональной квадратному корню высоты воды Н. Наличие квадратного корня в расходе воды приводит к нелинейной установке.

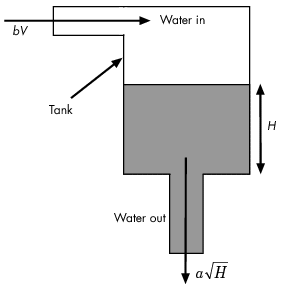
В следующей таблице описаны переменные, параметры, дифференциальные уравнения, состояния, входы и выходы системы водоемов.

Переменные	H - высота воды в резервуаре. Vol - объём воды в баке. V - напряжение, приложенное к насосу.
Параметры	А - площадь поперечного сечения резервуара. b - постоянная, связанная с расходом в резервуар. а - постоянная, связанная с расходом из резервуара.
Дифференциальное уравнение	$\frac{}{} ddtVol = \frac{}{} AdHdt = \sqrt{}$ bV − aH
Государства	H
Исходные данные	V
Продукция	H

Требования к конструкции

Высота воды в баке, H, должны соответствовать следующим требованиям ответа на шаг:

Время нарастания менее 2,5 секунд
Время установки менее 20 секунд
Перерасход менее 5%

Укажите требования к ответу на шаг

Откройте модель Simulink.

sys = 'watertank_stepinput';
open_system(sys);

Регистрировать уровень воды, H.
Во время оптимизации модель моделируется с использованием текущего значения параметров модели, а регистрируемый сигнал используется для оценки проектных требований.
```
PlantOutput = Simulink.SimulationData.SignalLoggingInfo;
PlantOutput.BlockPath               = [sys '/Water-Tank System'];
PlantOutput.OutputPortIndex         = 1;
PlantOutput.LoggingInfo.NameMode    = 1;
PlantOutput.LoggingInfo.LoggingName = 'PlantOutput';
```
Сохраните данные регистрации.
```
simulator = sdo.SimulationTest(sys);
simulator.LoggingInfo.Signals = PlantOutput;
```
simulator является sdo.SimulationTest объект, который также используется позже для моделирования модели.
Укажите требования к ответу на шаг.
```
StepResp = sdo.requirements.StepResponseEnvelope;
StepResp.RiseTime = 2.5;
StepResp.SettlingTime = 20;
StepResp.PercentOvershoot = 5;
StepResp.FinalValue = 2;
StepResp.InitialValue = 1;
```
StepResp является sdo.requirements.StepResponseEnvelope объект. Значения, присвоенные StepResp.FinalValue и StepResp.InitialValue соответствуют ступенчатому изменению высоты резервуара для воды от 1 кому 2.

Задание конструктивных переменных

При оптимизации отклика модели программа изменяет значения параметров (конструктивных переменных) в соответствии с требованиями проекта.

Выберите параметры модели для оптимизации. Здесь оптимизируйте параметры PID-контроллера.
```
p = sdo.getParameterFromModel(sys,{'Kp','Ki'});
```
p является массивом из 2 param.Continuous объекты.
Чтобы ограничить параметры положительными значениями, задайте минимальное значение каждого параметра равным 0.
```
p(1).Minimum = 0;
p(2).Minimum = 0;
```

Оптимизация реакции модели

Создайте конструкторскую функцию для оценки производительности системы для набора значений параметров.
```
evalDesign = @(p) sldo_model1_design(p,simulator,StepResp);
```
evalDesign является анонимной функцией, вызывающей функцию затрат sldo_model1_design. Функция затрат моделирует модель и оценивает требования к конструкции.
Совет
Напечатать edit sldo_model1_design для просмотра этой функции.
Оцените текущий ответ. (Необязательно)
1. Вычислите отклик модели, используя текущие значения конструктивных переменных.
  initDesign = evalDesign(p);
  Во время моделирования блок Step Response выдает предупреждения об утверждении в подсказке MATLAB ®, которые указывают на то, что требования, указанные в блоке, не удовлетворяются.
2. Изучите нелинейные ограничения неравенства.
  initDesign.Cleq
  ans = 0.1739 0.0169 -0.0002 -0.0101 -0.0229 0.0073 -0.0031 0.0423
  Некоторые Cleq значения являются положительными, за пределами заданного допуска, что указывает на то, что реакция с использованием текущих значений параметров нарушает проектные требования.
Укажите параметры оптимизации.
```
opt = sdo.OptimizeOptions;
opt.MethodOptions.Algorithm = 'sqp';
```
Программное обеспечение настраивается opt для использования метода оптимизации по умолчанию, fminconи алгоритм последовательного квадратичного программирования для fmincon.
Оптимизируйте ответ.
```
[pOpt,optInfo] = sdo.optimize(evalDesign,p,opt);
```
При каждой итерации оптимизации программа моделирует модель и решатель оптимизации по умолчанию. fmincon изменяет конструктивные переменные в соответствии с требованиями проекта. Дополнительные сведения см. в разделе Как алгоритм оптимизации формулирует проблемы минимизации.
После завершения оптимизации в окне команд отображаются следующие результаты:
```
                               max        Step-size    First-order 
 Iter F-count        f(x)   constraint                 optimality
    0      5            0       0.1739
    1     10            0      0.03411            1         0.81
    2     15            0            0        0.235       0.0429
    3     15            0            0     2.26e-18            0
Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the selected value of the function tolerance,
and constraints are satisfied to within the selected value of the constraint tolerance.
```
Сообщение Local minimum found that satisfies the constraints указывает, что решатель оптимизации нашел решение, удовлетворяющее проектным требованиям в пределах заданных допусков. Дополнительные сведения о выводах, отображаемых во время оптимизации, см. в разделе Итерационное отображение.
Проверьте информацию о завершении оптимизации, содержащуюся в optInfo выходной аргумент. Эта информация помогает убедиться, что ответ соответствует требованиям ответа на шаг.
Например, проверьте следующие поля:
- Cleq, которая показывает оптимизированные нелинейные ограничения неравенства.
  optInfo.Cleq
  ans = -0.0001 -0.0028 -0.0050 -0.0101 -0.0135 -0.0050 -0.0050 -0.0732
  Все значения удовлетворяют Cleq ≤ 0 в пределах допусков оптимизации, что указывает на то, что требования ответа на шаг удовлетворяются.
- exitflag, который определяет причину завершения оптимизации.
  Значение: 1, что указывает на то, что решатель нашел решение, которое было меньше указанных допусков на значение функции и нарушения ограничений.

Просмотрите оптимизированные значения параметров.

pOpt

pOpt(1,1) =
 
       Name: 'Kp'
      Value: 2.0545
    Minimum: 0
    Maximum: Inf
       Free: 1
      Scale: 1
       Info: [1x1 struct]

 
pOpt(2,1) =
 
       Name: 'Ki'
      Value: 0.3801
    Minimum: 0
    Maximum: Inf
       Free: 1
      Scale: 1
       Info: [1x1 struct]

Моделирование модели с оптимизированными значениями.
1. Обновите оптимизированные значения параметров в модели.
  sdo.setValueInModel(sys,pOpt);
2. Моделирование модели.
  sim(sys);

См. также

Документация