Документация

Загрузить данные образца.

Загрузите образец продольных данных.

load longitudinalData

Матрица Y содержит данные ответа для 16 человек. Ответ представляет собой уровень лекарственного средства в крови, измеренный в пять временных точек (t = 0, 2, 4, 6 и 8). Каждая строка Y соответствует отдельному объекту, и каждый столбец соответствует временному моменту. Первые восемь субъектов - женщины, а вторые восемь субъектов - мужчины. Это смоделированные данные.

Данные графика.

Постройте график данных по всем 16 предметам.

figure()
t = [0,2,4,6,8];
plot(t,Y)
hold on

hf = plot(t,Y(1:8,:),'^');
hm = plot(t,Y(9:16,:),'o');
legend([hf(1),hm(1)],'Female','Male','Location','NorthEast')

title('Longitudinal Response')
ylabel('Blood Drug Level')
xlabel('Time')
hold off

Определите матрицы проектирования.

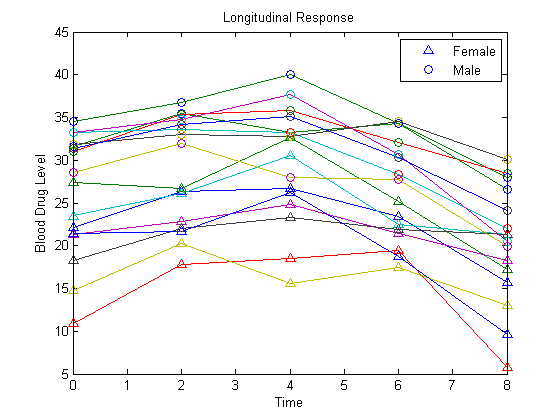
Пусть _yij обозначает ответ для отдельного i = 1,..., n, измеренный в моменты _{времени tij}, j = 1,..., d. В этом примере n = 16 и d = 5. Пусть Gi обозначает пол отдельного i, где Gi = 1 для мужчин и 0 для женщин.

Рассмотрите возможность установки квадратной продольной модели с отдельным наклоном и пересечением для каждого пола.

где $${}_{\mathrm{\alpha i}}={}_{(\mathrm{}}\alpha i1,{.}_{..}{,}^{}\mathrm{\alpha id})\mathrm{\prime }$$∼MVN (0, Λ). Корреляция ошибок учитывает кластеризацию внутри отдельного пользователя.

Подгонка этой модели с помощью mvregressданные ответа должны быть в n-за-d матрице. Y уже находится в правильном формате.

Затем создайте массив ячеек длиной n матриц конструкции d-by-K. Для этой модели существует K = 6 параметров.

Для отдельных i матрица проектирования 5 на 6

соответствующий вектору параметров

Матрица X1 имеет матрицу дизайна для самки, и X2 имеет матрицу дизайна для самца.

Создание массива ячеек матриц проектирования. Первые восемь особей - самки, а вторые восемь - самцы.

X = cell(8,1);
X(1:8) = {X1};
X(9:16) = {X2};

Подгоните модель.

Подгоните модель, используя максимальную оценку правдоподобия. Отображение расчетных коэффициентов и стандартных ошибок.

[b,sig,E,V,loglikF] = mvregress(X,Y);
[b sqrt(diag(V))]

ans =

   18.8619    0.7432
   13.0942    1.0511
    2.5968    0.2845
   -0.3771    0.0398
   -0.5929    0.4023
    0.0290    0.0563

Коэффициенты на условиях взаимодействия (в последних двух строках b) не кажутся значимыми. Для этой подгонки можно использовать значение целевой функции loglikeability, loglikF, чтобы сравнить эту модель с моделью без условий взаимодействия, используя тест отношения правдоподобия.

Печать подогнанной модели.

Постройте подгоняемые линии для самок и самцов.

Yhatf = X1*b;
Yhatm = X2*b;

figure()
plot(t,Y)
hold on

plot(t,Y(1:8,:),'^',t,Y(9:16,:),'o')

hf = plot(t,Yhatf,'k--','LineWidth',3);
hm = plot(t,Yhatm,'k','LineWidth',3);
legend([hf,hm],'Females','Males','Location','NorthEast')

title('Longitudinal Response')
ylabel('Blood Drug Level')
xlabel('Time')
hold off

Определите уменьшенную модель.

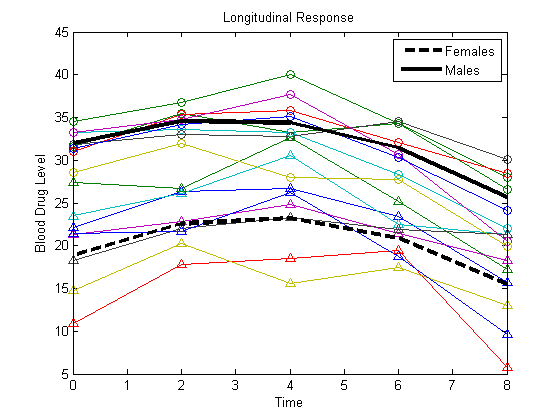
Подогнать модель без условий взаимодействия,

где $${}_{\mathrm{\alpha i}}={}_{(\mathrm{}}\alpha i1,{.}_{..}{,}^{}\mathrm{\alpha id})\mathrm{\prime }$$∼MVN (0, Λ).

Эта модель имеет четыре коэффициента, которые соответствуют первым четырем столбцам матриц проектирования X1 и X2 (для женщин и мужчин соответственно).

X1R = X1(:,1:4);
X2R = X2(:,1:4);

XR = cell(8,1);
XR(1:8) = {X1R};
XR(9:16) = {X2R};

Подгоните уменьшенную модель.

Подгоните эту модель, используя максимальную оценку правдоподобия. Отображение расчетных коэффициентов и их стандартных ошибок.

[bR,sigR,ER,VR,loglikR] = mvregress(XR,Y);
[bR,sqrt(diag(VR))]

ans =

   19.3765    0.6898
   12.0936    0.8591
    2.2919    0.2139
   -0.3623    0.0283

Проведите тест отношения правдоподобия.

Сравните две модели, используя тест отношения правдоподобия. Нулевая гипотеза заключается в том, что уменьшенная модель достаточна. Альтернатива заключается в том, что уменьшенная модель является неадекватной (по сравнению с полной моделью с терминами взаимодействия).

Статистика теста отношения правдоподобия сравнивается с хи-квадратным распределением с двумя степенями свободы (для двух понижаемых коэффициентов).

LR = 2*(loglikF-loglikR);
pval = 1 - chi2cdf(LR,2)

pval =

    0.0803