Документация

Загрузить данные образца.

Загрузите данные панели образца.

load panelData

Массив наборов данных, panelData, содержит ежегодные наблюдения по восьми городам в течение 6 лет. Это смоделированные данные.

Определите переменные.

Первая переменная, Growth, измеряет экономический рост (переменная ответа). Вторая и третья переменные - это показатели города и года соответственно. Последняя переменная, Employ, измеряет занятость (переменная предиктора).

y = panelData.Growth;
city = panelData.City;
year = panelData.Year;
x = panelData.Employ;

Печать данных, сгруппированных по категориям.

Чтобы найти потенциальные фиксированные эффекты для конкретного города, создайте рамочный график ответа, сгруппированный по городу.

figure()
boxplot(y,city)
xlabel('City')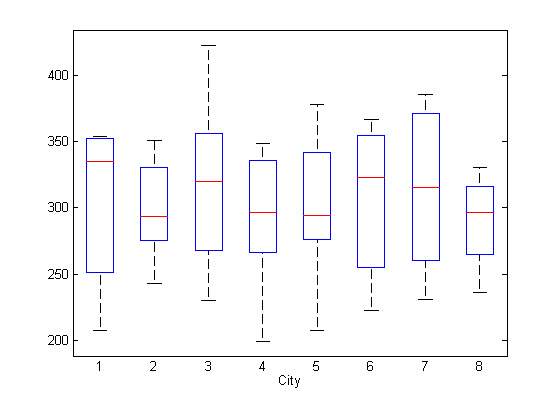

По-видимому, не существует каких-либо систематических различий в средних показателях реагирования между городами.

Печать данных, сгруппированных по другой категории.

Чтобы найти потенциальные фиксированные эффекты для конкретного года, создайте рамочный график ответа, сгруппированного по годам.

figure()
boxplot(y,year)
xlabel('Year')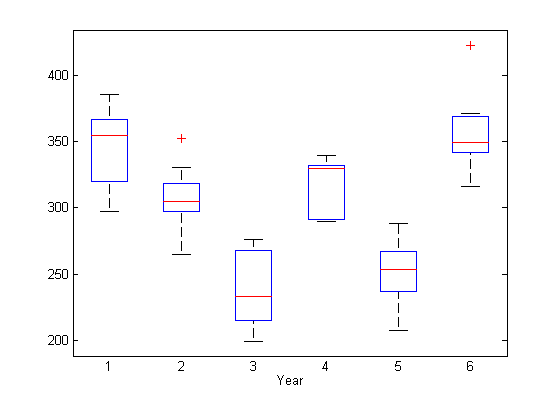

Некоторые свидетельства систематических различий в среднем ответе между годами, похоже, существуют.

Форматирование данных ответа.

Пусть _yij обозначает ответ для города j = 1,..., d, в году i = 1,..., n. Аналогично, _xij является соответствующим значением прогнозирующей переменной. В этом примере n = 6 и d = 8.

Рассмотрите возможность установки модели фиксированных эффектов для конкретного года с постоянным наклоном и параллельной корреляцией между городами в том же году.

где $${}_{\mathrm{\alpha i}}={}_{(\mathrm{}}\alpha i1,{.}_{..}{,}^{}\mathrm{\alpha id})\mathrm{\prime }$$∼MVN (0, Λ). Параллельная корреляция учитывает любые неизмеренные, статические по времени факторы, которые могут аналогичным образом повлиять на рост в некоторых городах. Например, города с близкой пространственной близостью с большей вероятностью будут иметь аналогичный экономический рост.

Подгонка этой модели с помощью mvregress, переформатировать данные ответа в матрицу n-за-d.

n = 6; d = 8;
Y = reshape(y,n,d);

Форматирование матриц проектирования.

Создайте массив ячеек длиной n матриц конструкции d-by-K. Для этой модели существуют параметры K = 7 (d = 6 членов пересечения и наклон).

Предположим, вектор параметров расположен как

В этом случае первая матрица проектирования для 1 года выглядит как

и вторая матрица дизайна для года 2 выглядит как

Матрицы проектирования на оставшиеся 4 года аналогичны.

K = 7; N = n*d;
X = cell(n,1);
for i = 1:n
    x0 = zeros(d,K-1);
    x0(:,i) = 1;
    X{i} = [x0,x(i:n:N)];
end

Подгоните модель.

Подгонка модели с использованием обычных наименьших квадратов (OLS).

[b,sig,E,V] = mvregress(X,Y,'algorithm','cwls');
b

b =

   41.6878
   26.1864
  -64.5107
   11.0924
  -59.1872
   71.3313
    4.9525

Печать подогнанной модели.

xx = linspace(min(x),max(x));
axx = repmat(b(1:K-1),1,length(xx));
bxx = repmat(b(K)*xx,n,1);
yhat =  axx + bxx;

figure()
hPoints = gscatter(x,y,year);
hold on
hLines = plot(xx,yhat);
for i=1:n  
   set(hLines(i),'color',get(hPoints(i),'color'));
end
hold off

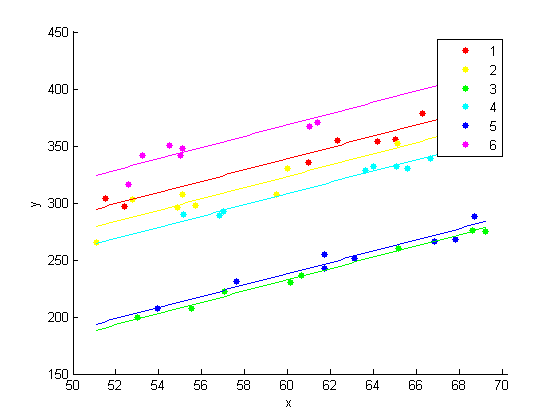
Модель с годовыми перехватами и общим наклоном, по-видимому, вполне соответствует данным.

Остаточная корреляция.

Постройте график остатков, сгруппированных по годам.

figure()
gscatter(year,E(:),city)
ylabel('Residuals')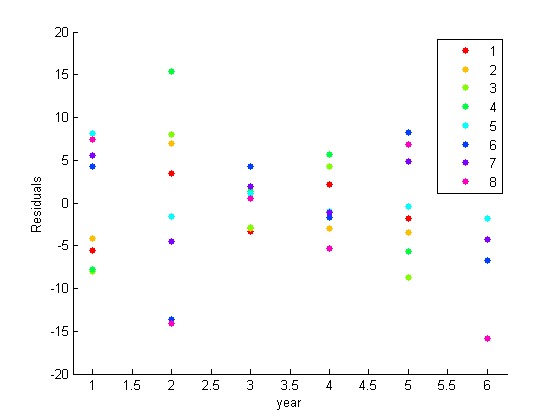

Остаточный график предполагает наличие параллельной корреляции. Например, города 1, 2, 3 и 4 последовательно выше или ниже среднего в группе в любом данном году. То же самое относится и к сбору городов 5, 6, 7 и 8. Как видно на разведочных участках, систематических последствий для конкретных городов не наблюдается.

Панель исправила стандартные ошибки.

Для вычисления скорректированных панелью стандартных ошибок для коэффициентов регрессии используйте матрицу оцененная дисперсия-ковариация ошибок.

XX = cell2mat(X);
S = kron(eye(n),sig);
Vpcse = inv(XX'*XX)*XX'*S*XX*inv(XX'*XX);
se = sqrt(diag(Vpcse))

se =

    9.3750
    8.6698
    9.3406
    9.4286
    9.5729
    8.8207
    0.1527