Подгонка многомерной модели линейной регрессии с использованием mvregress, необходимо настроить матрицу ответа и матрицы проектирования определенным образом. Правильно отформатированные входные данные, mvregress может обрабатывать различные проблемы многомерной регрессии.
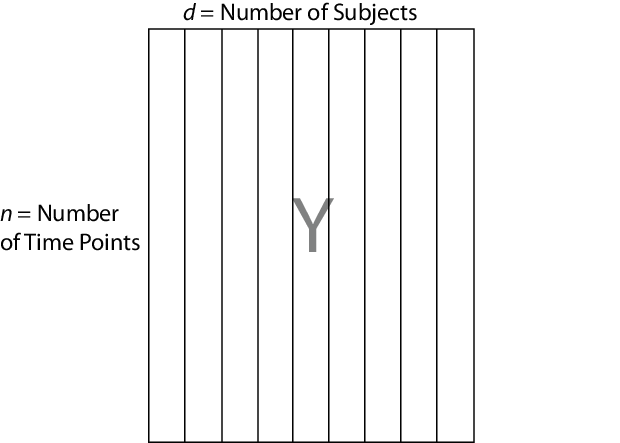
mvregress ожидает, что n наблюдений потенциально коррелированных d-мерных откликов будут в n-за-d-матрицей, названной Y, например. То есть настройте ответы так, чтобы структура зависимостей находилась между наблюдениями в одной строке. При указании Y как вектор длиной n (вектор строки или столбца), то mvregress предполагает, что d = 1, и рассматривает элементы как n независимых наблюдений. Он не моделирует вектор как одну реализацию коррелированного ряда (например, временного ряда).
Чтобы проиллюстрировать, как настроить матрицу ответа, предположим, что ваши многомерные ответы являются повторными измерениями, выполненными на субъектах в несколько моментов времени, как показано на следующем рисунке.
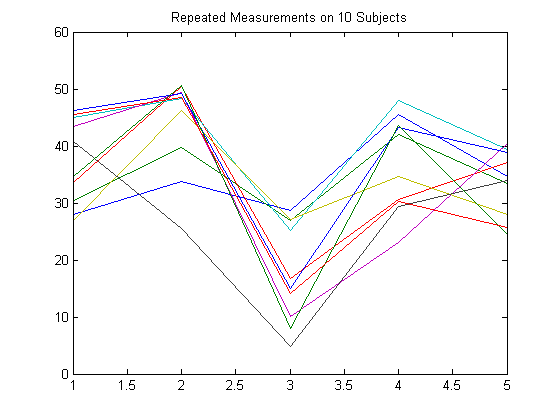
Предположим, что наблюдения внутри субъекта коррелируются.
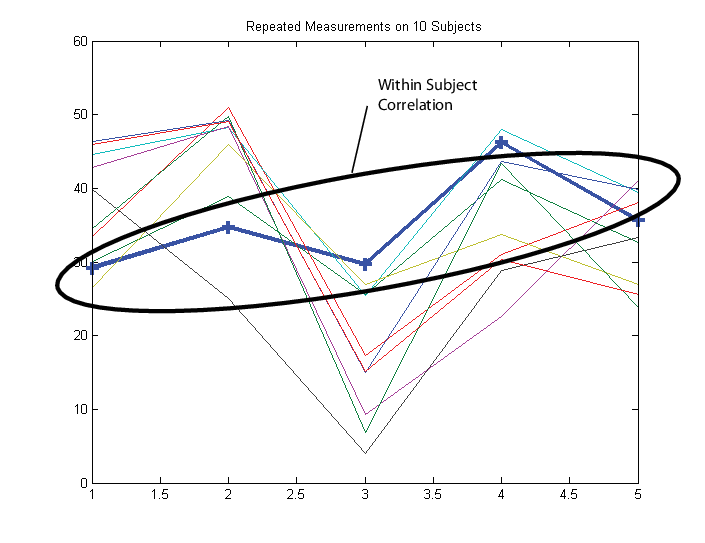
В этом случае настройте матрицу ответа Y так, что каждая строка соответствует субъекту, а каждый столбец соответствует временной точке.

Затем снова предположим, что наблюдения, сделанные по предметам одновременно, коррелируются (параллельная корреляция).
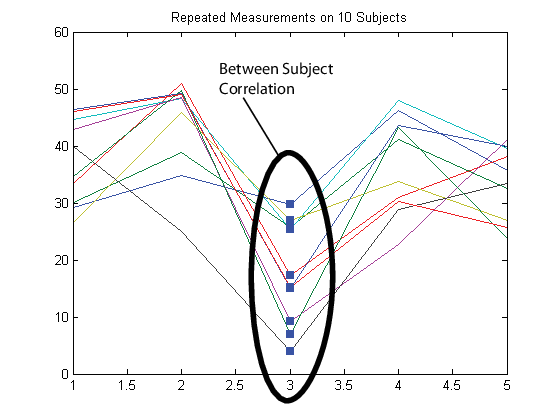
В этом случае настройте матрицу ответа Y так, что каждая строка соответствует временной точке, и каждый столбец соответствует теме.
В многомерной модели линейной регрессии каждый d-мерный отклик имеет соответствующую матрицу дизайна. В зависимости от модели матрица дизайна может состоять из экзогенных переменных предиктора, фиктивных переменных, запаздывающих ответов или комбинации этих и других ковариационных терминов.
Если d > 1 и все d измерения имеют одинаковую матрицу конструкции, то укажите одну матрицу конструкции n-by-p, где p - число переменных предиктора. Чтобы определить пересечение для каждого размера, добавьте столбец из них в матрицу конструкции. В этом случае mvregress применяет матрицу проектирования ко всем размерам d.
Если d > 1 и все d размеры не имеют одной матрицы конструкции, укажите матрицы конструкции, используя массив ячеек длиной n массивов d-by-K, с именем X, например. K - общее число коэффициентов регрессии в модели. Обратите внимание, что строки массивов в X соответствуют столбцам матрицы ответа, Y.
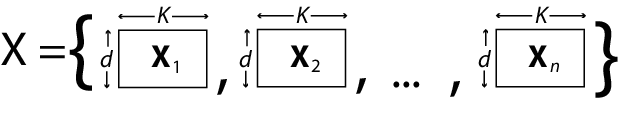
Если все n наблюдений имеют одинаковую матрицу конструкции, можно указать массив ячеек, содержащий одну матрицу конструкции d-by-K. В этом случае mvregress применяет матрицу проектирования ко всем n наблюдениям. Например, эта ситуация может возникнуть, если предикторы являются функциями времени, и все наблюдения измерялись в одни и те же моменты времени.
В частном случае, когда d = 1, можно указать одну матрицу конструкции n-by-K (не в массиве ячеек). Однако следует рассмотреть возможность использования fitlm чтобы соответствовать регрессионным моделям для одномерных, непрерывных ответов.
В следующих разделах показано, как настроить некоторые общие проблемы многомерной регрессии для оценки с использованием mvregress.
Многомерная общая линейная модель имеет вид
+ 1) × d + En × d.
В расширенном виде
То есть каждый d-мерный отклик имеет переменные перехвата и p-предсказателя, и каждый размер имеет свой собственный набор коэффициентов регрессии. В этом виде решением наименьших квадратов является B = X\Y. Оценка этой модели с помощью mvregressиспользуйте матрицу n-за-d ответов, как описано выше.
Если все размеры d имеют одинаковую матрицу конструкции, используйте матрицу конструкции n-by- (p + 1), как описано выше. Добавление столбца единиц к переменным p-предиктора вычисляет пересечение для каждого измерения.
Если все размеры d не имеют одинаковой матрицы конструкции, переформатируйте матрицу конструкции n-by- (p + 1) в массив ячеек длины n матриц d-by-K. Здесь K = (p + 1) d для пересечения и откосов для каждого размера.
Например, предположим, что n = 4, d = 3 и p = 2 (два условия предиктора в дополнение к перехвату). На этом рисунке показано форматирование i-го элемента в массиве ячеек.
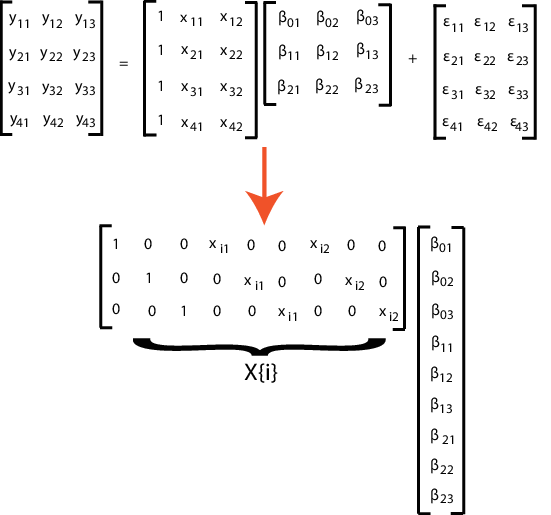
Если вы предпочитаете, вы можете изменить форму вектора K-by-1 коэффициентов обратно в (p + 1) -by-d матрицу после оценки.
Чтобы наложить ограничения на параметры модели, настройте матрицу конструкции соответствующим образом. Например, предположим, что три размера в предыдущем примере имеют общий уклон. То есть β13 = = β23 = β2. В этом случае каждая матрица проектирования является 3 на 5, как показано на следующем рисунке.
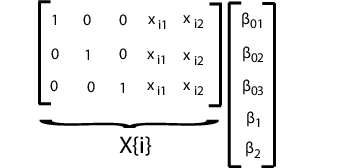
В продольном анализе вы можете измерить ответы по n субъектам в d временных точках с корреляцией между наблюдениями, сделанными по одному и тому же предмету. Например, предположим, что вы измеряете ответы yij в моменты времени tij, i = 1,..., n и j = 1,..., d. Кроме того, предположим, что каждый субъект находится в одной из двух групп (таких как мужчина или женщина), определяемых индикаторной переменной Gi. Вы можете смоделировать yij как функцию Gi и tij, с групповыми перехватами и уклонами, следующим образом:
..., n; j = 1,..., d,
где
∼MVN (0, Λ).
Большинство продольных моделей включают время как явный предиктор.
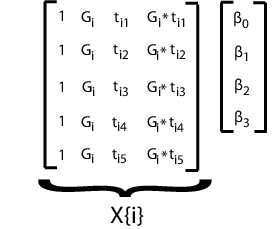
Подгонка этой модели с помощью mvregress, упорядочить ответы в n-за-d матрице, где n - количество субъектов, а d - количество моментов времени. Задайте матрицы конструкции в массиве ячеек n-длины матриц d-by-K, где здесь K = 4 для четырех коэффициентов регрессии.
Например, предположим, что d = 5 (пять наблюдений на субъекта). i-я матрица конструкции и соответствующий вектор параметров для указанной модели показаны на следующем рисунке.
В групповом анализе вы можете измерить ответы и ковариаты на d субъектов (таких как отдельные лица или страны) в n моментов времени. Например, предположим, что вы измеряете ответы ytj и ковариаты xtj для субъектов j = 1,..., d в моменты времени t = 1,..., n. Модель панели фиксированных эффектов со специфическими фиксированными эффектами и параллельной корреляцией может выглядеть следующим образом:
+ αtj,
где
(0, Λ).
В отличие от продольных моделей, модель панельного анализа обычно включает ковариаты, измеренные в каждый момент времени, вместо использования времени в качестве явного предиктора.
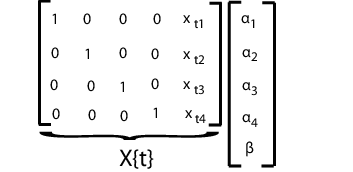
Подгонка этой модели с помощью mvregress, упорядочить ответы в n-за-d матрице так, чтобы каждый столбец соответствовал субъекту. Задайте матрицы проектирования в массиве ячеек длиной n из матриц d-by-K, где K = d + 1 для d перехватов и члена наклона.
Например, предположим, что d = 4 (четыре субъекта). Tth расчетная матрица и соответствующий вектор параметров показаны на следующем рисунке.
В, казалось бы, не связанной регрессии (SUR), вы моделируете d отдельные регрессии, каждая с собственным перехватом и наклоном, но общей матрицей дисперсии-ковариации ошибок. Например, предположим, что вы измеряете отклики yij и ковариаты xij для регрессионных моделей j = 1,..., d, с i = 1,..., n наблюдениями, чтобы соответствовать каждой регрессии. Модель SUR может выглядеть следующим образом:
+ αij,
где
∼MVN (0, Λ).
Эта модель очень похожа на многомерную общую линейную модель, за исключением того, что она имеет различные ковариаты для каждого измерения.
Подгонка этой модели с помощью mvregress, упорядочить ответы в n-за-d-матрицей, так что каждый столбец имеет данные для j-й регрессионной модели. Задайте матрицы проектирования в массиве ячеек длиной n из матриц d-by-K, где K = 2d для d перехватов и d откосов.
Например, предположим, что d = 3 (три регрессии). i-я расчетная матрица и соответствующий вектор параметров показаны на следующем рисунке.
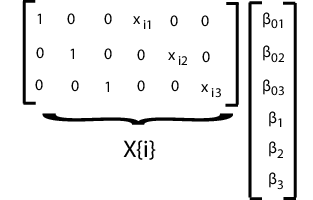
Векторная авторегрессионная модель VAR (p) выражает d-мерные отклики временных рядов как линейную функцию p запаздывающих d-мерных откликов от предыдущих времен. Например, предположим, что вы измеряете ответы ytj для временных рядов j = 1,..., d в моменты времени t = 1,..., n. Модель VAR (p) может выглядеть следующим образом:
где
(0, Λ).
При оценке векторных авторегрессивных моделей, как правило, необходимо использовать первые p-наблюдения для инициирования модели или предоставить некоторые другие значения ответа предварительной выборки.
Подгонка этой модели с помощью mvregress, расположить ответы в n-за-d матрице так, чтобы каждый столбец соответствовал временному ряду. Задайте матрицы конструкции в массиве ячеек длиной n из матриц d-by-K, где K = d + pd2.
Например, предположим, что d = 2 (два временных ряда) и p = 1 (одно запаздывание). Tth расчетная матрица и соответствующий вектор параметров показаны на следующем рисунке.
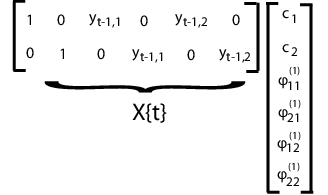
В качестве альтернативы, Econometrics Toolbox™ имеет функции для подгонки и прогнозирования моделей VAR (p), включая опцию для указания экзогенных переменных предиктора.