В этом примере показано, как проверить значительные различия между категорией (группой) означает использование t-теста, двустороннего анализа ANOVA (дисперсионный анализ) и анализа ANOCOVA (ковариационный анализ).
Цель - определить, зависит ли ожидаемая миля на галлон для автомобиля от десятилетия, в котором он был изготовлен, или места, где он был изготовлен.
Примечание
nominal и ordinal типы данных массива не рекомендуются. Для представления упорядоченных и неупорядоченных дискретных нечисловых данных используйте тип данных Категориальные массивы.
load('carsmall')
unique(Model_Year)ans =
70
76
82Переменная MPG имеет мили на галлон измерений на выборке из 100 автомобилей. Переменные Model_Year и Origin содержат модельный год и страну происхождения для каждого автомобиля.
Первый фактор интереса - десятилетие производства. Данные содержат три года производства.
Создать порядковый массив с именем Decade путем объединения наблюдений за годы 70 и 76 в категорию с меткой 1970sи положив наблюдения из 82 в категорию с меткой 1980s.
Decade = ordinal(Model_Year,{'1970s','1980s'},[],[70 77 82]);
getlevels(Decade)ans =
1970s 1980s Нарисуйте рамочный график миль на галлон, сгруппированный по десятилетию производства.
figure()
boxplot(MPG,Decade)
title('Miles per Gallon, Grouped by Decade of Manufacture')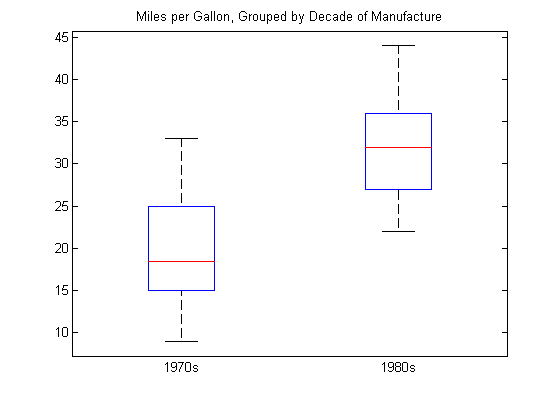
Бокс-сюжет предполагает, что мили на галлон выше в автомобилях, произведённых в 1980-е годы по сравнению с 1970-ми годами.
Вычислите среднее значение и дисперсию миль на галлон за каждое десятилетие.
[xbar,s2,grp] = grpstats(MPG,Decade,{'mean','var','gname'})xbar =
19.7857
31.7097
s2 =
35.1429
29.0796
grp =
'1970s'
'1980s'Этот результат показывает, что среднее значение миль на галлон в 1980-х годах было 31.71, по сравнению с 19.79 в 1970-е годы. Отклонения в двух группах одинаковы.
Провести t-тест с двумя выборками, предполагая равные дисперсии, чтобы проверить значительную разницу между групповыми средствами. Гипотеза такова
MPG70 = MPG(Decade=='1970s'); MPG80 = MPG(Decade=='1980s'); [h,p] = ttest2(MPG70,MPG80)
h =
1
p =
3.4809e-151 указывает, что нулевая гипотеза отклоняется на уровне значимости по умолчанию 0,05. Значение p для теста очень мало. Имеются достаточные доказательства того, что среднее значение миль на галлон в 1980-х годах отличается от среднего значения миль на галлон в 1970-х годах.Второй фактор интереса - место изготовления. Сначала преобразуйте Origin в номинальный массив.
Location = nominal(Origin); tabulate(Location)
tabulate(Location)
Value Count Percent
France 4 4.00%
Germany 9 9.00%
Italy 1 1.00%
Japan 15 15.00%
Sweden 2 2.00%
USA 69 69.00%Объединение категорий France, Germany, Italy, и Sweden в новую категорию с именем Europe.
Location = mergelevels(Location, ... {'France','Germany','Italy','Sweden'},'Europe'); tabulate(Location)
Value Count Percent
Japan 15 15.00%
USA 69 69.00%
Europe 16 16.00%Вычислите средние мили на галлон, сгруппированные по местоположению производства.
[xbar,grp] = grpstats(MPG,Location,{'mean','gname'})xbar =
31.8000
21.1328
26.6667
grp =
'Japan'
'USA'
'Europe'Этот результат показывает, что среднее количество миль на галлон является самым низким для выборки автомобилей, произведенных в США.
Проведите двустороннюю ANOVA для проверки различий в ожидаемых милях на галлон между уровнями факторов для Decade и Location.
Статистическая модель:
где MPGij - ответ, миль на галлон, для автомобилей, изготовленных в десятилетие i в местоположении j. Эффекты лечения для первого фактора, десятилетия производства, являются α i-членами (ограничены суммой до нуля). Эффекты лечения для второго фактора, местоположения производства, представляют собой β j-члены (ограничены суммой до нуля). αij являются некоррелированными, обычно распределенными шумовыми терминами.
Гипотезы для проверки - это равенство десятилетних эффектов,
αi≠0,
и равенство эффектов местоположения,
βj≠0.
Многофакторную ANOVA можно провести с помощью anovan.
anovan(MPG,{Decade,Location},'varnames',{'Decade','Location'});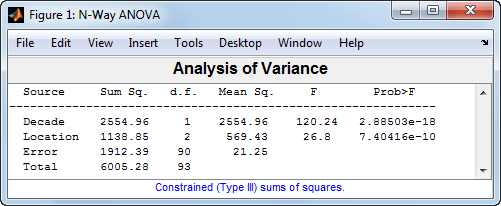
Этот результат показывает результаты двусторонней ANOVA. P-значение для проверки равенства эффектов десятилетия составляет 2.88503e-18таким образом, нулевая гипотеза отвергается на уровне значимости 0,05. P-значение для проверки равенства эффектов местоположения равно 7.40416e-10, поэтому эта нулевая гипотеза также отвергается.
Потенциальным нарушителем в этом анализе является вес автомобиля. Ожидается, что автомобили с большим весом будут иметь меньший пробег газа. Включить переменную Weight как непрерывный ковариат в ANOVA; то есть провести анализ ANOCOVA.
Предполагая параллельные линии, статистическая модель
= 1,..., 100.
Отличием этой модели от двусторонней модели ANOVA является включение непрерывного предиктора, Wewtijk, веса для k-го автомобиля, который был сделан в i-й декаде и в j-й локации. Параметр наклона - γ.
Добавьте непрерывный ковариат в качестве третьей группы во второй anovan входной аргумент. Использовать аргумент пары имя-значение Continuous чтобы указать, что Weight (третья группа) является непрерывной.
anovan(MPG,{Decade,Location,Weight},'Continuous',3,...
'varnames',{'Decade','Location','Weight'});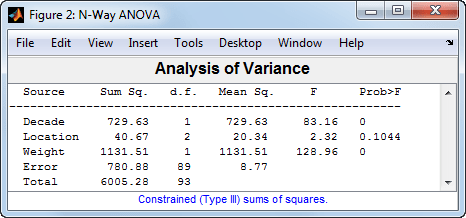
Этот результат показывает, что при учете веса автомобиля недостаточно доказательств влияния производственного местоположения (p-value = 0.1044).
Можно использовать интерактивный интерфейс aoctool изучить этот результат.
aoctool(Weight,MPG,Location);
Эта команда открывает три диалоговых окна. В диалоговом окне График прогнозирования ANOCOVA (ANOCOVA Prediction Plot) выберите модель отдельных средств.
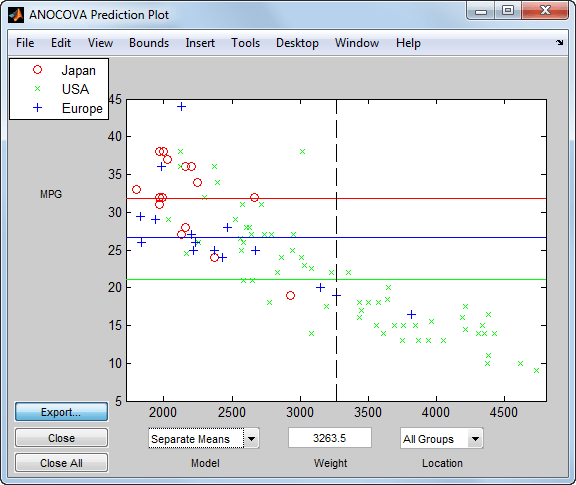
Эти выходные данные показывают, что если вы не включаете Weight в модели существуют довольно большие различия в ожидаемых милях на галлон среди трех производственных местоположений. При этом модель не корректируется на десятилетие производства.
Теперь выберите модель «Параллельные линии».
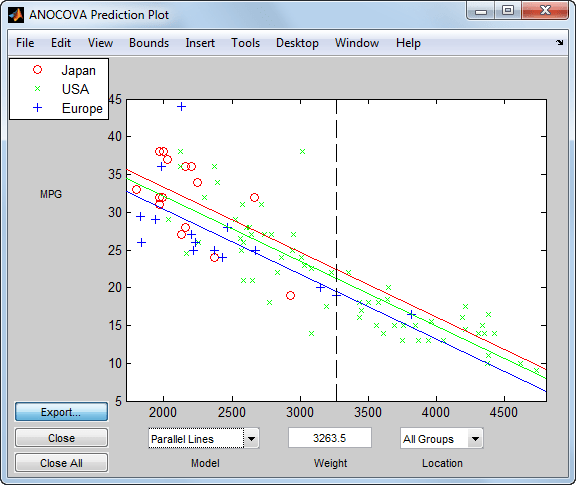
При включении Weight в модели разница в ожидаемых милях на галлон среди трех производственных мест значительно меньше.
anovan | aoctool | boxplot | grpstats | nominal | ordinal | ttest2