Дифференцирование

Чтобы проиллюстрировать, как взять производные с помощью программы Symbolic Math Toolbox™, сначала создайте символьное выражение:

syms x
f = sin(5*x);

Команда

diff(f)

дифференцируется f в отношении x:

ans =
5*cos(5*x)

В качестве другого примера позвольте

g = exp(x)*cos(x);

где exp(x) обозначает e^{x и} дифференцировать g:

y = diff(g)

y =
exp(x)*cos(x) - exp(x)*sin(x)

Найти производную от g для заданного значения x, заменить x для значения с использованием subs и возвращает числовое значение с помощью vpa. Найти производную от g в x = 2.

vpa(subs(y,x,2))

ans =
-9.7937820180676088383807818261614

Взять вторую производную от g, введите

diff(g,2)

ans =
-2*exp(x)*sin(x)

Вы можете получить один и тот же результат, взяв производную дважды:

diff(diff(g))

ans =
-2*exp(x)*sin(x)

В этом примере программное обеспечение MATLAB ® автоматически упрощает ответ. Однако в некоторых случаях MATLAB может не упростить ответ, и в этом случае можно использовать simplify команда. Пример такого упрощения см. в разделе Дополнительные примеры.

Обратите внимание, что для получения производной константы необходимо сначала определить константу как символическое выражение. Например, ввод

c = sym('5');
diff(c)

прибыль

ans =
0

Если просто ввести

diff(5)

Возврат MATLAB

ans =
     []

потому что 5 не является символическим выражением.

Производные выражений с несколькими переменными

Чтобы дифференцировать выражение, содержащее более одной символьной переменной, укажите переменную, которую необходимо дифференцировать относительно. diff затем вычисляет частную производную выражения относительно этой переменной. Например, учитывая символическое выражение

syms s t
f = sin(s*t);

команда

diff(f,t)

вычисляет $∂f/∂t$ частных производных. Результат:

ans = 
s*cos(s*t)

Дифференцироваться f относительно переменной s, введите

diff(f,s)

который возвращает:

ans =
t*cos(s*t)

Если переменная для дифференциации не указана, MATLAB выбирает переменную по умолчанию. В основном переменная по умолчанию - это буква, ближайшая к x в алфавите. Полный набор правил см. в разделе Поиск символьной переменной по умолчанию. В предыдущем примере: diff(f) принимает производную от f в отношении t потому что письмо t ближе к x в алфавите, чем буква s является. Чтобы определить переменную по умолчанию, отличную от MATLAB, используйте symvar:

symvar(f, 1)

ans = 
t

Вычислить вторую производную f в отношении t:

diff(f, t, 2)

Эта команда возвращает

ans =
-s^2*sin(s*t)

Обратите внимание, что diff(f, 2) возвращает тот же ответ, потому что t является переменной по умолчанию.

Другие примеры

Для дополнительной иллюстрации diff команда, определение a, b, x, n, t, и theta в рабочей области MATLAB путем ввода

syms a b x n t theta

Эта таблица иллюстрирует результаты ввода diff(f).

f	diff (f)
syms x n f = x^n;	diff(f) ans = n*x^(n - 1)
syms a b t f = sin(a*t + b);	diff(f) ans = acos(b + at)
syms theta f = exp(i*theta);	diff(f) ans = exp(theta1i)1i

Чтобы дифференцировать функцию Бесселя первого рода, besselj(nu,z), в отношении z, тип

syms nu z
b = besselj(nu,z);
db = diff(b)

который возвращает

db =
(nu*besselj(nu, z))/z - besselj(nu + 1, z)

diff функция также может принимать символьную матрицу в качестве своего входа. В этом случае дифференцирование выполняется поэлементно. Рассмотрим пример

syms a x
A = [cos(a*x),sin(a*x);-sin(a*x),cos(a*x)]

который возвращает

A =
[  cos(a*x), sin(a*x)]
[ -sin(a*x), cos(a*x)]

Команда

diff(A)

прибыль

ans =
[ -a*sin(a*x),  a*cos(a*x)]
[ -a*cos(a*x), -a*sin(a*x)]

Можно также выполнить дифференциацию векторной функции относительно векторного аргумента. Считайте преобразование от Евклидова (x, y, z) к сферическому $(r, λ,φ)$ координатами, как дано $x=rcosλcosφ$ , $y=rcosλsinϕ$ , и $z=rsinλ$ . Причем $λ$ соответствует отметке или широте, в то время как $λ$ обозначает азимут или долготу.

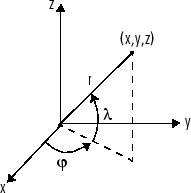
Чтобы вычислить матрицу якобиана J этого преобразования, используйте jacobian функция. Математическая запись для J

$J = \frac{\partial (x, y, z}{) \partial (r, λ}$ ,φ).

Для синтаксиса панели инструментов используйте l для $λ$ и f для $start$ . Команды

syms r l f
x = r*cos(l)*cos(f);
y = r*cos(l)*sin(f);
z = r*sin(l);
J = jacobian([x; y; z], [r l f])

вернуть якобиан

J =
[ cos(f)*cos(l), -r*cos(f)*sin(l), -r*cos(l)*sin(f)]
[ cos(l)*sin(f), -r*sin(f)*sin(l),  r*cos(f)*cos(l)]
[        sin(l),         r*cos(l),                0]

и команды

detJ = simplify(det(J))

прибыль

detJ = 
-r^2*cos(l)

Аргументы jacobian функция может быть вектором столбца или строки. При этом, поскольку определитель якобиана является довольно сложным тригонометрическим выражением, можно использовать simplify для выполнения тригонометрических замен и сокращений (упрощение).

Таблица, суммирующая diff и jacobian далее.

Математический оператор	Команда MATLAB
$\frac{}{dfdx}$	`diff(f)` или `diff(f, x)`
$\frac{}{dfda}$	`diff(f, a)`
$\frac{^{}}{^{d2fdb2}}$	`diff(f, b, 2)`
$\frac{J=\partial (r,}{t) \partial (}$ u, v)	`J = jacobian([r; t],[u; v])`

Документация