Подобно преобразованию Фурье, непрерывное вейвлет-преобразование (CWT) использует внутренние произведения для измерения подобия между сигналом и анализирующей функцией. В преобразовании Фурье анализирующие функции являются комплексными экспоненциальными, . Результирующее преобразование является функцией от одной переменной, λ. В кратковременном преобразовании Фурье анализирующие функции являются окнами комплексных экспоненциалов, ejstartt, и результат является функцией двух переменных. Коэффициенты STFT, start), представляют собой совпадение между сигналом и синусоидой с угловой частотой λ в интервале заданной длины, центрированном на,
В CWT анализирующая функция представляет собой вейвлет, CWT сравнивает сигнал со сдвинутыми и сжатыми или растянутыми версиями вейвлета. Растягивание или сжатие функции в совокупности называется расширением или масштабированием и соответствует физическому понятию масштаба. Сравнивая сигнал с вейвлетом в различных масштабах и положениях, можно получить функцию двух переменных. 2-D представление сигнала 1-D является избыточным. Если вейвлет является комплекснозначным, то CWT является комплекснозначной функцией масштаба и положения. Если сигнал имеет действительное значение, то CWT является действительной функцией масштаба и положения. Для параметра масштаба a > 0 и позиции b CWT имеет значение:
(t − ba) dt
где обозначает комплексный конъюгат. Не только значения масштаба и положения влияют на коэффициенты CWT, но и выбор вейвлета влияет на значения коэффициентов.
Непрерывно изменяя значения параметра масштабирования a и параметра положения b, получают коэффициенты cwt C (a, b). Следует отметить, что для удобства зависимость коэффициентов CWT от функции и анализирующего вейвлета была подавлена.
Умножение каждого коэффициента на соответствующим образом масштабированный и сдвинутый вейвлет дает составляющие вейвлеты исходного сигнала.
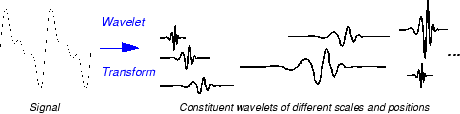
Существует много различных допустимых вейвлетов, которые могут использоваться в CWT. Хотя может показаться запутанным, что существует так много вариантов для анализирующего вейвлета, на самом деле это сила вейвлет-анализа. В зависимости от того, какие функции сигнала вы пытаетесь обнаружить, вы можете выбрать вейвлет, который облегчает обнаружение этой функции. Например, если вы пытаетесь обнаружить резкие разрывы в сигнале, вы можете выбрать один вейвлет. С другой стороны, если вы заинтересованы в поиске колебаний с гладкими онсетами и смещениями, вы можете выбрать вейвлет, который более точно соответствует этому поведению.
Как и понятие частоты, еще одним полезным свойством сигналов и изображений является масштаб. Например, можно проанализировать температурные данные на предмет изменений в различных масштабах. Вы можете посмотреть на изменения от года к году или от десятилетия к десятилетию. Конечно, вы можете исследовать более тонкие (повседневные) или более грубые изменения масштаба. Некоторые процессы обнаруживают интересные изменения в течение длительного времени или пространственных масштабах, которые не очевидны в малых временных или пространственных масштабах. Происходит и обратная ситуация. Некоторые из наших перцептивных способностей демонстрируют инвариантность масштаба. Вы узнаете людей, которых знаете, независимо от того, смотрите ли вы на большой портрет или на маленькую фотографию.
Чтобы выйти за рамки разговорных описаний, таких как «растягивание» или «усадка», мы вводим масштабный коэффициент, часто обозначаемый буквой a. Масштабный коэффициент является положительной величиной, a > 0. Для синусоид эффект масштабного коэффициента очень легко увидеть.
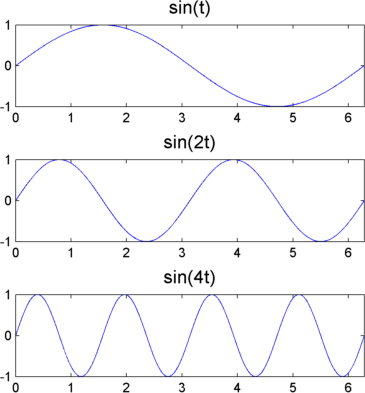
В sin (at) шкала является обратной радиановой частоте, a.
Масштабный коэффициент работает точно так же с вейвлетами. Чем меньше масштабный коэффициент, тем больше «сжимается» вейвлет. И наоборот, чем больше масштаб, тем больше растягивается вейвлет. Следующий рисунок иллюстрирует это для вейвлетов на весах 1,2 и 4.
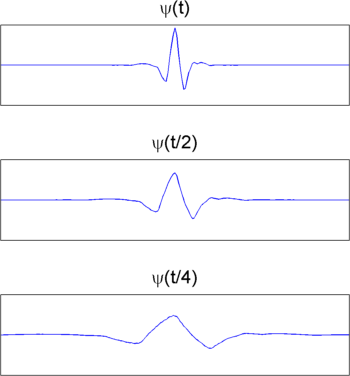
Эта общая обратная зависимость между масштабом и частотой сохраняется для сигналов в целом.
Представление в масштабе времени не только является другим способом просмотра данных, но и является вполне естественным способом просмотра данных, полученных из большого числа природных явлений.
Существует явная взаимосвязь между масштабом и частотой. Напомним, что более длинные шкалы соответствуют наиболее «растянутым» вейвлетам. Чем больше растягивается вейвлет, тем длиннее часть сигнала, с которой он сравнивается, и, следовательно, чем грубее характеристики сигнала, измеренные коэффициентами вейвлета.

Подводя итог, можно сказать, что общее соответствие между масштабом и частотой:
Малый масштаб a ⇒ Сжатый вейвлет ⇒ Быстро меняющиеся детали ⇒ Высокочастотный λ.
Long scale a ⇒ Растянутый вейвлет ⇒ Медленно меняющиеся, грубые характеристики ⇒ Low frequency λ.
Хотя существует общая взаимосвязь между масштабом и частотой, точной взаимосвязи не существует. Пользователи, знакомые с анализом Фурье, часто хотят определить отображение между вейвлетом в заданном масштабе с заданным периодом выборки и частотой в герцах. Сделать это можно только в общем смысле. Поэтому лучше говорить о псевдочастоте, соответствующей шкале. Программное обеспечение Vavelet Toolbox™ предоставляет две функции centfrq и scal2frq, которые позволяют найти эти приблизительные отношения масштаб-частота для указанных вейвлетов и масштабов.
Основной подход идентифицирует пиковую мощность в преобразовании Фурье вейвлета как его центральную частоту и делит это значение на произведение шкалы и интервала выборки. Посмотрите scal2frq для получения подробной информации. В следующем примере показано соответствие между расчетной частотой центра db8 вейвлет и синусоида одинаковой частоты.
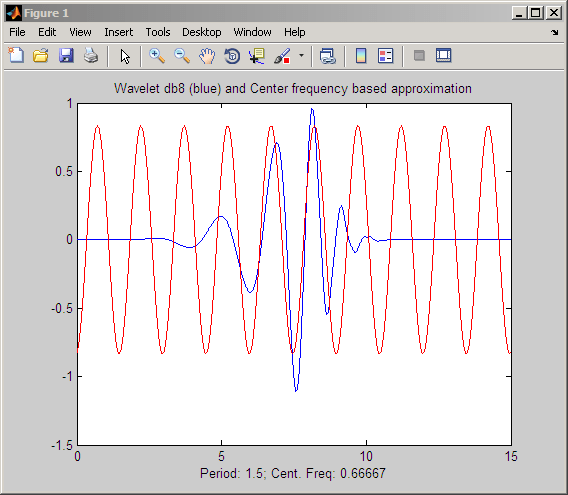
Взаимосвязь между масштабом и частотой в CWT также исследуется при непрерывном вейвлет-преобразовании в качестве полосового фильтра.
Сдвиг импульса просто означает задержку (или продвижение) его начала. Математически задержка функции f (t) на k представляется как f (t-k):
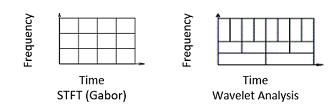
При преобразовании Фурье с коротким временем STFT описывается как окно сигнала для создания анализа локальной частоты. Недостатком STFT-подхода является то, что размер окна является постоянным. Есть компромисс в выборе размера окна. Более длинное временное окно улучшает частотное разрешение, в то же время приводя к худшему временному разрешению, поскольку преобразование Фурье теряет все временные разрешения по длительности окна. И наоборот, более короткое временное окно улучшает локализацию времени, в то же время приводя к ухудшению разрешения частоты.
Вейвлет-анализ представляет следующий логический шаг: метод оконной обработки с областями переменного размера. Вейвлет-анализ позволяет использовать длинные временные интервалы, где требуется более точная низкочастотная информация, и более короткие области, где требуется высокочастотная информация.

На следующем рисунке показаны различные способы разложения частотно-временной плоскости STFT и вейвлет-анализа.