Поскольку CWT является избыточным преобразованием и коэффициенты CWT зависят от вейвлета, может быть трудно интерпретировать результаты.
Чтобы помочь вам в интерпретации коэффициентов CWT, лучше всего начать с простого сигнала для анализа и анализирующего вейвлета с простой структурой.
Признаком сигнала, который вейвлеты очень хорошо обнаруживают, является прерывистость, или сингулярность. Резкие переходы в сигналах приводят к вейвлет-коэффициентам с большими абсолютными значениями.
Для сигнала создать сдвинутый импульс. Импульс возникает в точке 500.
x = zeros(1000,1); x(500) = 1;
Для вейвлета выберите вейвлет Хаара.
[~,psi,xval] = wavefun('haar',10);
plot(xval,psi); axis([0 1 -1.5 1.5]);
title('Haar Wavelet');
Для вычисления CWT с использованием вейвлета Хаара в масштабах от 1 до 128 введите:
CWTcoeffs = cwt(x,1:128,'haar');
CWTcoeffs представляет собой матрицу 128 на 1000. Каждая строка матрицы содержит коэффициенты CWT для одной шкалы. Есть 128 строк, потому что SCALES вход в cwt является 1:128. Размер столбца матрицы соответствует длине входного сигнала.
Напомним, что CWT 1D сигнала является функцией параметров масштаба и положения. Чтобы создать график коэффициентов CWT, постройте график положения вдоль оси x, масштабируйте вдоль оси y и закодируйте величину или размер коэффициентов CWT как цвет в каждой точке плоскости x-y или во временной шкале.
Этот график можно создать с помощью cwt с необязательным входным аргументом 'plot'.
cwt(x,1:128,'haar','plot'); colormap jet; colorbar;
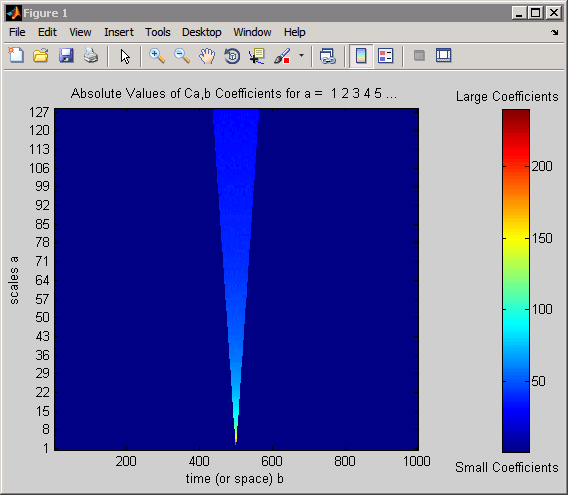
Предыдущий рисунок был модифицирован текстовыми метками, чтобы явно показать, какие цвета указывают большие и малые коэффициенты CWT.
Можно также построить график размера коэффициентов CWT в 3D с
cwt(x,1:64,'haar','3Dplot'); colormap jet;
Исследуя CWT сдвинутого импульсного сигнала, можно увидеть, что набор больших коэффициентов CWT сосредоточен в узкой области во временной плоскости при малых масштабах, центрированных вокруг точки 500. По мере увеличения шкалы набор больших коэффициентов CWT становится шире, но остается центрированным вокруг точки 500. Если вы отслеживаете границу этой области, она напоминает следующий рисунок.
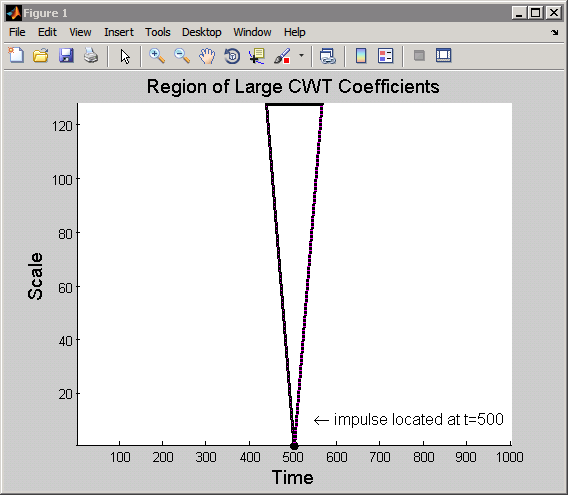
Эта область называется конусом влияния точки t = 500 для импульса Хаара. Для данной точки конус влияния показывает, на какие коэффициенты CWT влияет значение сигнала в этой точке.
Чтобы понять конус влияния, предположим, что на [-C, C] поддерживается вейвлет. Смещение вейвлета на b и масштабирование на a приводит к тому, что вейвлет поддерживается на [-Ca + b, Ca + b]. Для простого случая перемещенного (t−τ), коэффициенты CWT только отличные от нуля в интервале вокруг τ, равного поддержке небольшой волны в каждом масштабе. Это можно увидеть, рассматривая формальное выражение CWT смещенного импульса.
dt=1aψ* (τ−ba)
Для импульса коэффициенты CWT равны сопряженному, обращенному во времени и масштабированному вейвлету как функции параметра сдвига, b. Это можно увидеть на графике коэффициентов CWT для нескольких выбранных шкал.
subplot(311)
plot(CWTcoeffs(10,:)); title('Scale 10');
subplot(312)
plot(CWTcoeffs(50,:)); title('Scale 50');
subplot(313)
plot(CWTcoeffs(90,:)); title('Scale 90');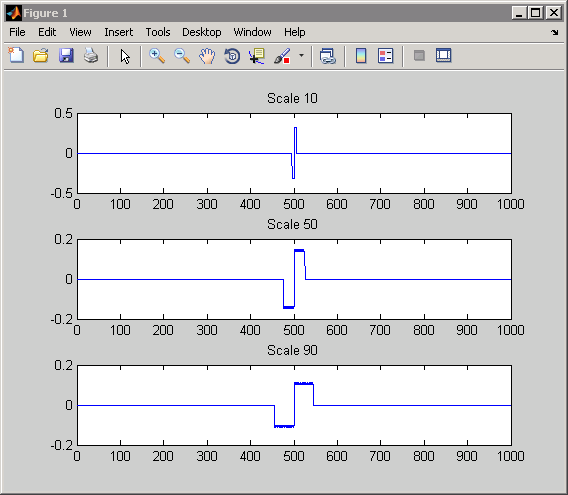
Конус воздействия зависит от импульса. Вы можете найти и нарисовать конус влияния для конкретного вейвлета с помощью conofinf.
Следующий пример характеризует суперпозицию двух сдвинутых импульсов, t − 500). В этом случае используйте экстремальный фазовый вейвлет Daubechies с четырьмя моментами исчезновения ,db4. На следующем рисунке показан конус воздействия для точек 300 и 500 с использованием db4 вейвлет.
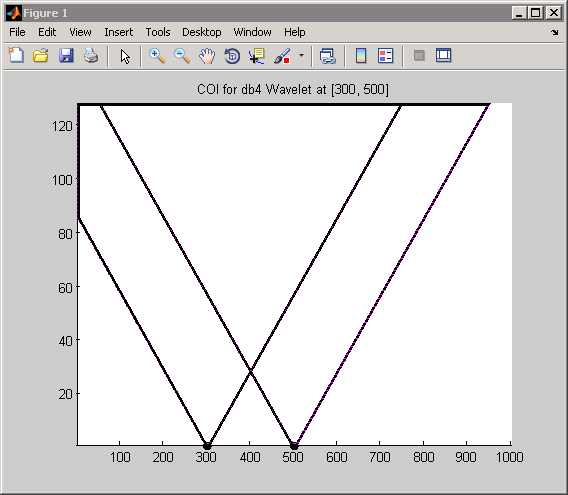
Посмотрите на точку 400 для шкалы 20. В этом масштабе можно видеть, что ни один из конусов влияния не перекрывает точку 400. Поэтому можно ожидать, что коэффициент CWT будет равен нулю в этой точке и шкале. Сигнал является ненулевым только при двух значениях, 300 и 500, и ни один из конусов влияния для этих значений не включает точку 400 в шкале 20. Вы можете подтвердить это, введя:
x = zeros(1000,1); x([300 500]) = 1; CWTcoeffs = cwt(x,1:128,'db4'); plot(CWTcoeffs(20,:)); grid on;
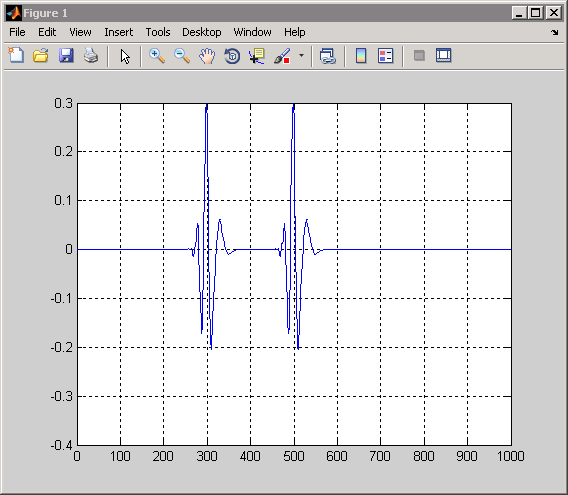
Затем взгляните на точку 400 по шкале 80. В шкале 80 конусы воздействия для обеих точек 300 и 500 включают точку 400. Даже если сигнал равен нулю в точке 400, получается ненулевой коэффициент CWT в этой шкале. Коэффициент CWT является ненулевым, поскольку поддержка вейвлета стала достаточно большой при этой шкале, чтобы позволить значениям сигнала 100 баллов выше и ниже влиять на коэффициент CWT. Вы можете подтвердить это, введя:
plot(CWTcoeffs(80,:)); grid on;
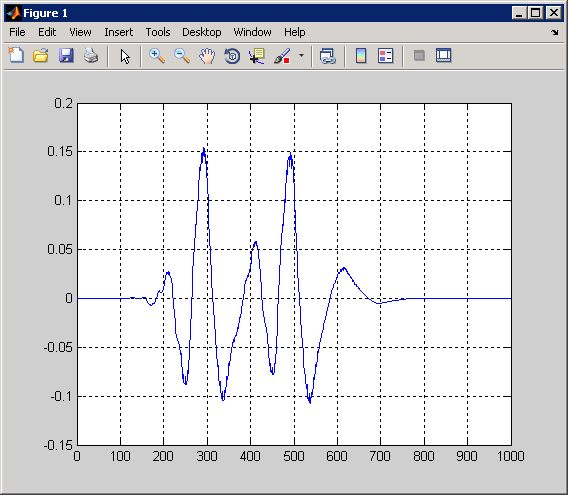
В предыдущем примере коэффициенты CWT стали большими вблизи резкого изменения сигнала. Эта способность обнаруживать разрывы является силой вейвлет-преобразования. Предыдущий пример также продемонстрировал, что коэффициенты CWT лучше всего локализуют разрыв в малых масштабах. При малых масштабах малая поддержка вейвлета гарантирует, что сингулярность влияет только на небольшой набор вейвлет-коэффициентов.
Чтобы продемонстрировать, почему вейвлет-преобразование является таким умелым в обнаружении резких изменений в сигнале, рассмотрим сдвинутый сигнал Heaviside или единичный шаг.
x = [zeros(500,1); ones(500,1)]; CWTcoeffs = cwt(x,1:64,'haar','plot'); colormap jet;
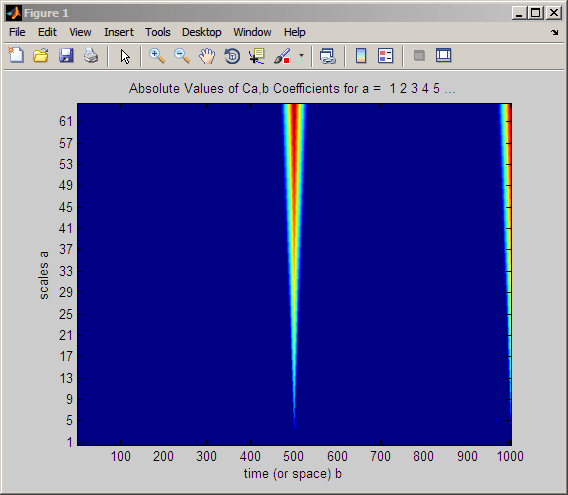
Подобно примеру сдвинутого импульса, резкий переход в сдвинутой ступенчатой функции приводит к большим коэффициентам CWT в разрыве. На следующем рисунке показано, почему это происходит.

На предыдущем рисунке красная функция является сдвинутой единичной ступенчатой функцией. Черные функции, обозначенные A, B и C, изображают вейвлеты Хаара в том же масштабе, но в разных положениях. Можно видеть, что коэффициенты CWT вокруг позиции A равны нулю. Сигнал равен нулю в этой окрестности, и поэтому вейвлет-преобразование также равно нулю, поскольку любой вейвлет интегрируется в ноль.
Обратите внимание на импульс Хаара, центрированный вокруг положения В. Отрицательная часть импульса Хаара перекрывается с областью ступенчатой функции, которая равна 1. Коэффициенты CWT являются отрицательными, поскольку произведение вейвлета Хаара и единичного шага является отрицательной константой. Интеграция по этой области дает отрицательное число.
Отметим, что импульс Хаара центрирован вокруг положения С. Здесь коэффициенты CWT равны нулю. Ступенчатая функция равна единице. Произведение вейвлета с функцией шага равно вейвлету. Интеграция любого вейвлета над его опорой равна нулю. Это свойство нулевого момента вейвлетов.
В положении В вейвлет Хаара уже сдвинулся в ненулевую часть ступенчатой функции на 1/2 ее опоры. Как только поддержка вейвлета пересекается с единичной частью ступенчатой функции, коэффициенты CWT являются ненулевыми. Фактически, ситуация, показанная на предыдущем рисунке, совпадает с тем, что коэффициенты CWT достигают своего наибольшего абсолютного значения. Это происходит потому, что весь отрицательный прогиб вейвлет-колебания перекрывается с единичной частью единичного шага, в то время как ни один из положительных прогибов вейвлета не происходит. Как только импульс сдвигается до такой степени, что положительное отклонение перекрывается с единичным шагом, будет некоторый положительный вклад в интеграл. Вейвлет-коэффициенты все еще отрицательные (отрицательная часть интеграла больше по площади), но они меньше по абсолютной величине, чем полученные в положении В.
На следующем рисунке показаны две другие позиции, где вейвлет пересекает единичную часть единичного шага.
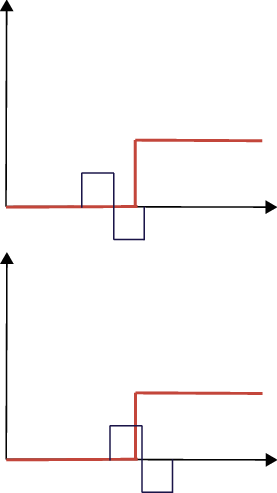
На верхней фигуре вейвлет только начал перекрываться с единичной частью единичного шага. В этом случае коэффициенты CWT являются отрицательными, но не такими большими в абсолютном значении, как те, которые получены в положении В. На нижнем чертеже вейвлет сдвинулся за положение В, и положительное отклонение вейвлета начинает вносить вклад в интеграл. Коэффициенты CWT все еще являются отрицательными, но не такими большими в абсолютном значении, как те, которые получены в положении B.
Теперь можно визуализировать, как вейвлет-преобразование может обнаруживать разрывы. Вы также можете визуализировать в этом простом примере, почему коэффициенты CWT являются отрицательными в CWT сдвинутого единичного шага, используя вейвлет Хаара. Обратите внимание, что это поведение отличается для других вейвлетов.
x = [zeros(500,1); ones(500,1)];
CWTcoeffs = cwt(x,1:64,'haar','plot'); colormap jet;
% plot a few scales for visualization
subplot(311);
plot(CWTcoeffs(5,:)); title('Scale 5');
subplot(312);
plot(CWTcoeffs(10,:)); title('Scale 10');
subplot(313);
plot(CWTcoeffs(50,:)); title('Scale 50');Далее рассмотрим, как CWT представляет плавные сигналы. Поскольку синусоидальные колебания являются обычным явлением, в этом разделе рассматривается, как синусоидальные колебания в сигнале влияют на коэффициенты CWT. Для начала рассмотрим sym4 вейвлет в определенном масштабе, наложенный на синусоидальную волну.
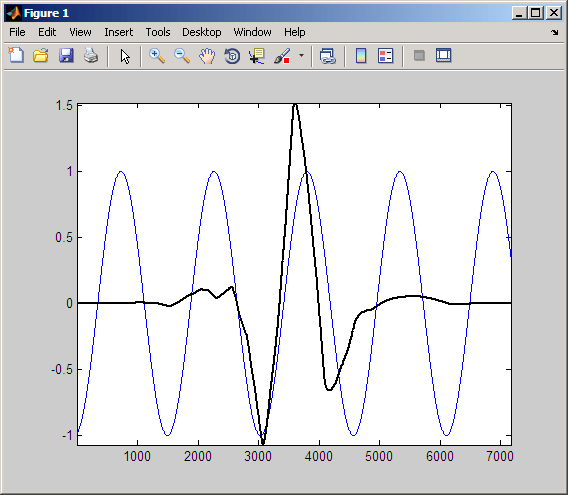
Напомним, что коэффициенты CWT получают вычислением произведения сигнала со сдвинутым и масштабированным анализирующим вейвлетом и интегрированием результата. На следующем рисунке показано произведение вейвлета и синусоиды от предыдущего рисунка.
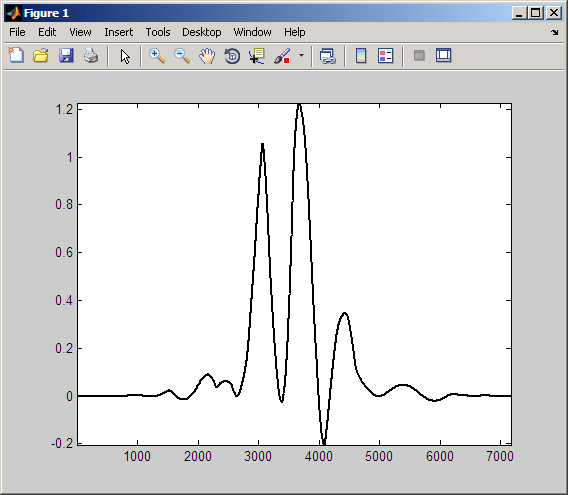
Можно видеть, что интеграция над этим продуктом дает положительный коэффициент CWT. Это происходит потому, что колебание в вейвлете приблизительно совпадает с периодом синусоидальной волны. Вейвлет находится в фазе с синусоидальной волной. Отрицательные отклонения импульса приблизительно совпадают с отрицательными отклонениями синусоидальной волны. То же самое относится и к положительным отклонениям как вейвлета, так и синусоиды.
На следующем рисунке смещается вейвлет 1/2 периода синусоидальной волны.
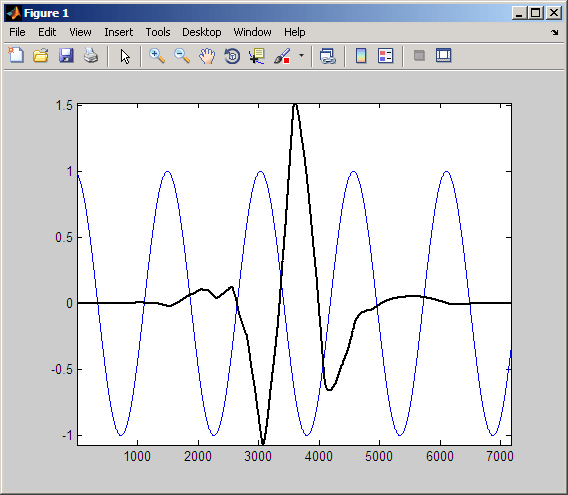
Осмотрите произведение сдвинутого импульса и синусоиды.
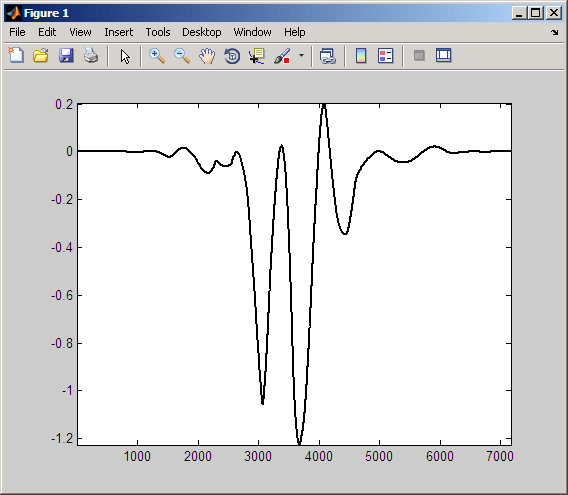
Можно видеть, что интеграция над этим продуктом дает отрицательный коэффициент CWT. Это происходит потому, что вейвлет находится в 1/2 цикла вне фазы с синусоидальной волной. Отрицательные отклонения импульса приблизительно совпадают с положительными отклонениями синусоидальной волны. Положительные отклонения импульса приблизительно совпадают с отрицательными отклонениями синусоиды.
Наконец, сдвигают вейвлет приблизительно на четверть цикла синусоидальной волны.
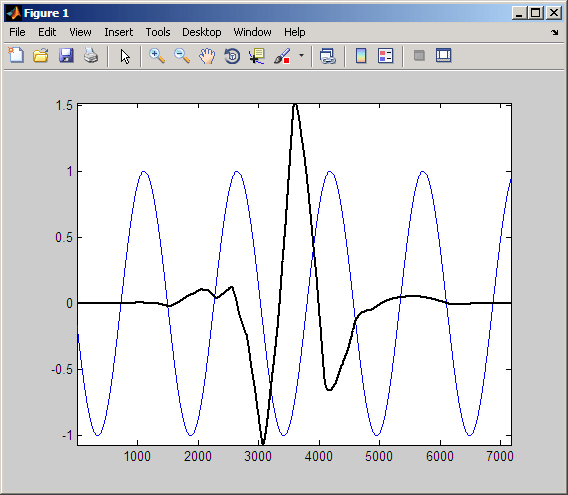
На следующем рисунке показано произведение сдвинутого вейвлета и синусоиды.
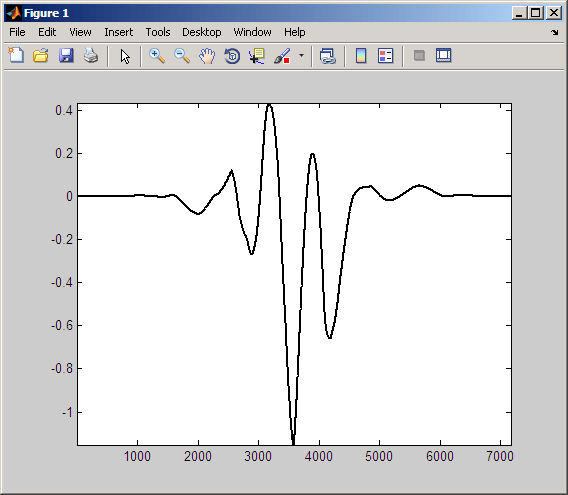
Интеграция по этому продукту дает коэффициент CWT, значительно меньший по абсолютной величине, чем любой из двух предыдущих примеров. Это происходит потому, что отрицательное отклонение импульса приблизительно выравнивается с положительным отклонением синусоидальной волны. Кроме того, основное положительное отклонение импульса приблизительно выравнивается с положительным отклонением синусоидальной волны. Полученный продукт выглядит гораздо более похожим на вейвлет, чем два других продукта. Если бы он выглядел точно как вейвлет, интеграл был бы равен нулю.
В весах, где колебание в вейвлете происходит либо в гораздо большем, либо в меньшем масштабе, чем период синусоидальной волны, получаем коэффициенты CWT, близкие к нулю. Следующий рисунок иллюстрирует случай, когда вейвлет колеблется в гораздо меньшем масштабе, чем синусоида.
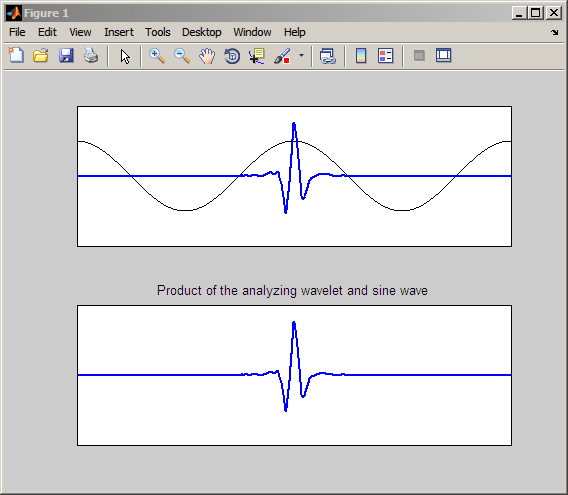
Изделие, показанное на нижней панели, сильно напоминает анализирующий вейвлет. Интеграция этого продукта приводит к коэффициенту CWT, близкому к нулю.
Следующий пример строит волну синуса на 60 Гц и получает CWT, используя sym8 вейвлет.
t = linspace(0,1,1000); x = cos(2*pi*60*t); CWTcoeffs = cwt(x,1:64,'sym8','plot'); colormap jet;
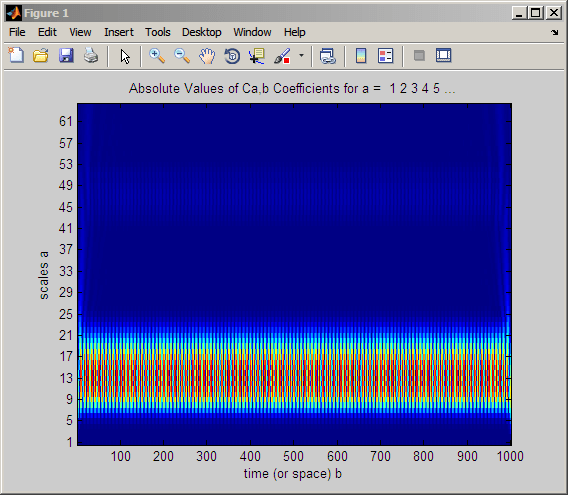
Следует отметить, что коэффициенты CWT являются большими в абсолютном значении вокруг шкал, 9 21. Псевдочастоты, соответствующие этим масштабам, можно найти с помощью команды:
freq = scal2frq(9:21,'sym8',1/1000);
Следует отметить, что коэффициенты CWT являются большими в масштабах, близких к частоте синусоидальной волны. Синусоидальный рисунок можно четко увидеть в коэффициентах CWT на этих шкалах с помощью следующего кода.
surf(CWTcoeffs); colormap jet;
shading('interp'); view(-60,12);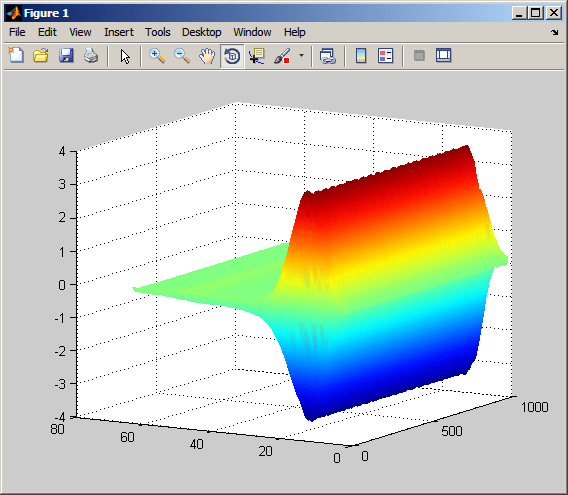
Последний пример строит сигнал, состоящий как из резких переходов, так и из плавных колебаний. Сигнал представляет собой 2-Hz синусоиду с двумя введенными разрывами.
N = 1024;
t = linspace(0,1,1024);
x = 4*sin(4*pi*t);
x = x - sign(t - .3) - sign(.72 - t);
plot(t,x); xlabel('t'); ylabel('x');
grid on;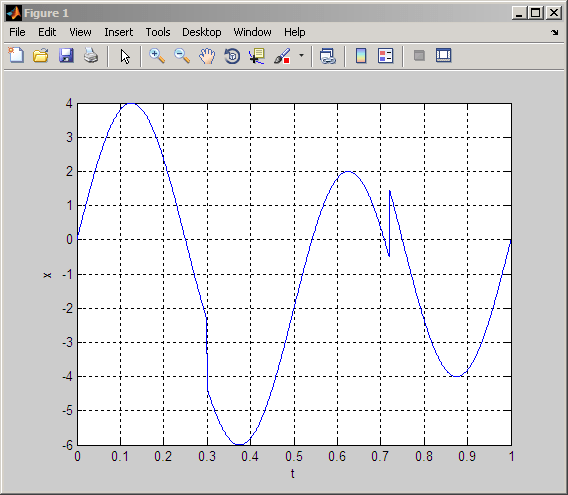
Обратите внимание на разрывы около t = 0,3 и t = 0,7.
Получение и построение графика CWT с помощью sym4 вейвлет.
CWTcoeffs = cwt(x,1:180,'sym4');
imagesc(t,1:180,abs(CWTcoeffs));
colormap jet; axis xy;
xlabel('t'); ylabel('Scales');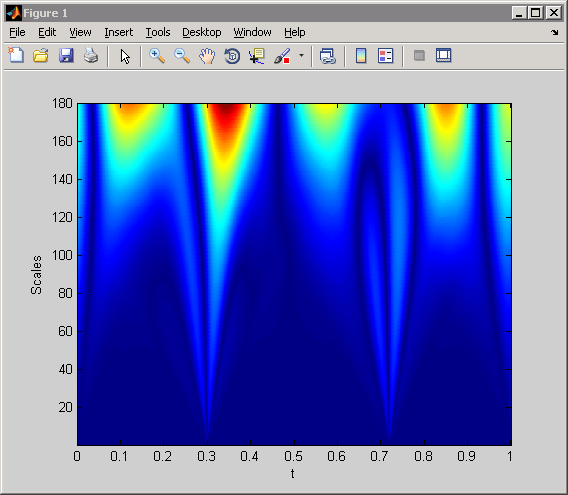
Следует отметить, что CWT обнаруживает как резкие переходы, так и колебания в сигнале. Резкие переходы влияют на коэффициенты CWT во всех масштабах и явно отделяют себя от более гладких сигнальных признаков в малых масштабах. С другой стороны, максимумы и минимумы 2-Hz синусоиды очевидны в коэффициентах CWT при больших масштабах и не очевидны при малых масштабах.
При интерпретации коэффициентов CWT важно учитывать следующие общие принципы.
Конус воздействия - в зависимости от шкалы на коэффициент CWT в точке могут влиять значения сигнала в удаленных точках. Необходимо учитывать поддержку вейвлета в определенных масштабах. Использоватьconofinf определить конус воздействия. Не все вейвлеты равны в своей поддержке. Например, вейвлет Хаара имеет меньшую поддержку во всех масштабах, чем sym4 вейвлет.
Обнаружение резких переходов - вейвлеты очень полезны для обнаружения резких изменений в сигнале. Резкие изменения в сигнале создают относительно большие вейвлет-коэффициенты (в абсолютном значении), центрированные вокруг разрыва во всех масштабах. Из-за поддержки вейвлета набор коэффициентов CWT, на которые влияет сингулярность, увеличивается с увеличением шкалы. Напомним, это определение конуса влияния. Наиболее точная локализация разрыва на основе коэффициентов CWT получается при наименьших масштабах.
Обнаружение признаков плавного сигнала - признаки плавного сигнала создают относительно большие вейвлет-коэффициенты в масштабах, где колебание в вейвлете лучше всего коррелирует с признаком сигнала. Для синусоидальных колебаний коэффициенты CWT отображают колебательную картину в масштабах, где колебание в вейвлете аппроксимирует период синусоидальной волны .
Основным алгоритмом для непрерывного вейвлет-преобразования (CWT) является:
Возьмите вейвлет и сравните его с участком в начале исходного сигнала.
Вычислите число, C, что представляет, насколько тесно коррелирован вейвлет с этим участком сигнала. Чем больше число C в абсолютном значении, чем больше сходство. Это следует из того, что коэффициенты CWT вычисляются с внутренним продуктом. Дополнительные сведения о том, как внутренние продукты измеряют сходство, см. в разделе Внутренние продукты. Если энергия сигнала и энергия импульса равны единице, C может быть интерпретирован как коэффициент корреляции. Следует отметить, что в общем случае энергия сигнала не равна единице, и коэффициенты CWT не могут непосредственно интерпретироваться как коэффициенты корреляции.
Как описано в непрерывных и дискретных вейвлет-преобразованиях, коэффициенты CWT явно зависят от анализирующего вейвлета. Поэтому коэффициенты CWT различаются при вычислении CWT для одного и того же сигнала с использованием различных вейвлетов.
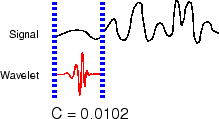
Переместите вейвлет вправо и повторите шаги 1 и 2 до тех пор, пока не будет охвачен весь сигнал.
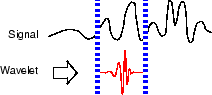
Масштабируйте (растягивайте) вейвлет и повторите шаги 1- 3.
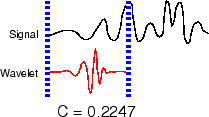
Повторите шаги 1-4 для всех масштабов.